---

跳转汇总链接

👉🔗动态规划算法汇总链接

---

优化在后面！

2.5 最长定差子序列

🔗题目链接

给你一个整数数组 arr 和一个整数 difference，请你找出并返回 arr 中最长等差子序列的长度，该子序列中相邻元素之间的差等于 difference 。
子序列 是指在不改变其余元素顺序的情况下，通过删除一些元素或不删除任何元素而从 arr 派生出来的序列。

1. 状态表示
   • dp[i] 表示，以 i 位置元素为结尾的所有子序列中，最长子序列的长度
2. 状态转移方程
   • 略（简单，不清楚的可以翻看之前的题解）
3. 初始化
   • 略
4. 填表顺序
   • 略
5. 返回值
   • 略

说的通但跑不通的代码：

class Solution {
public:
    int longestSubsequence(vector<int>& arr, int difference) {
        int n = arr.size();
        vector<int> dp(n, 1);
        int retMax = 1;
        for(int i = 1; i < n; i++)
        {
            for(int j = 0; j < i; j++)
            {
                if(arr[i] - arr[j] == difference)
                {
                    dp[i] = dp[j] + 1;
                }
            }
            retMax = max(retMax, dp[i]);
        }
        return retMax;
    }
};

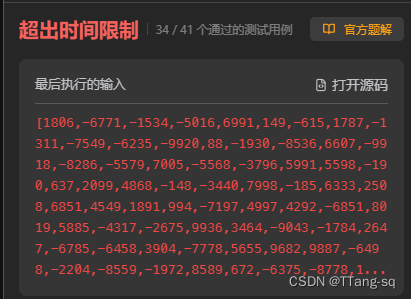
写到这里本人都以为只是一个练手题
…
直到
…

…
…

只好拿出 hash，再来一遍

• 优化
  • 将 <arr[]元素, dp[]> 的值绑定放在 hash 表中
  • 直接在 hash 中进行动态规划操作

🐎代码如下：

class Solution {
public:
    int longestSubsequence(vector<int>& arr, int difference) {
        unordered_map<int, int> hash;   // arr, dp
        hash[arr[0]] = 1;               // 初始化
        int retMax = 1;
        
        for(int i = 1; i < arr.size(); i++)
        {
            hash[arr[i]] = hash[arr[i] - difference] + 1;
            retMax = max(retMax, hash[arr[i]]);
        }
        return retMax;
    }
};

---

🥰如果本文对你有些帮助，欢迎👉 点赞 收藏 关注，你的支持是对作者大大莫大的鼓励！！(✿◡‿◡) 若有差错恳请留言指正~~

---