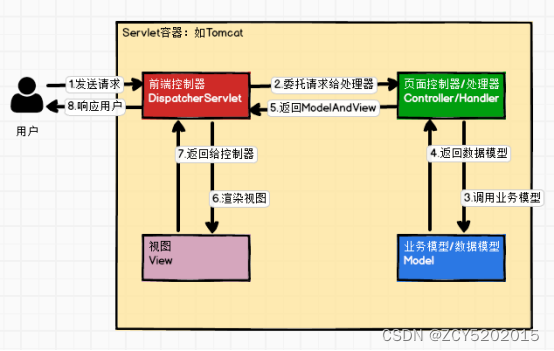
自注意力机制与卷积结合:On the Integration of Self-Attention and Convolution(CVPR2022)
引言
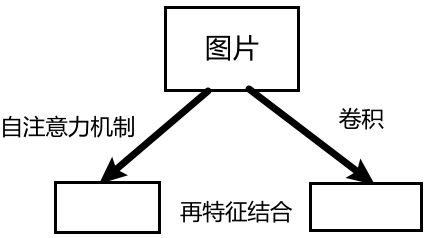
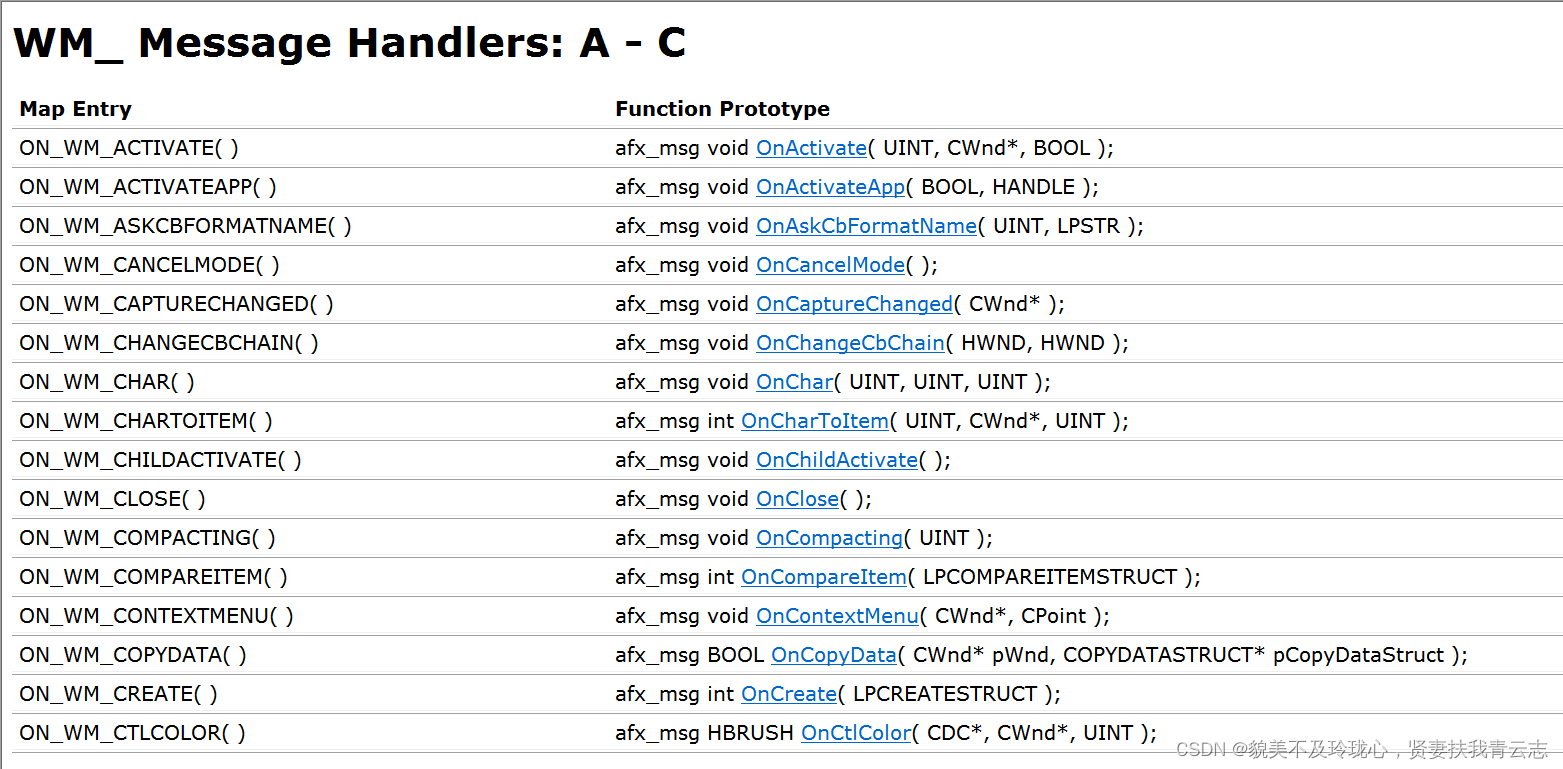
1:卷积可以接受比较大的图片的,但自注意力机制如果图片特别大的话,运算规模会特别大,即上图中右边(卷积)会算得比较快,左边(自注意力机制)会算得比较慢,所以我们要想些办法让自注意力机制规模小一点,本篇文章就只让qkv计算部分区域,而不是整个全局图片了。
2:自注意力机制中的qkv与卷积中的卷积核(比如说3x3的卷积核)能否一起得到?额,好像两者不是一类东西,但如果qkv用1x1的卷积核话,似乎有可能..
但是1x1的卷积核与3x3的卷积核似乎很难配套,有没有可能将3x3的卷积核用9个1x1的卷积核去替代呢?那既然两者(自注意力机制与卷积)都用到1x1的卷积,不妨两者共享1x1的卷积?
3. Revisiting Convolution and Self-Attention
3.1. Convolution
原理
这里先不扎进去研究论文上的公式,先用图看原理

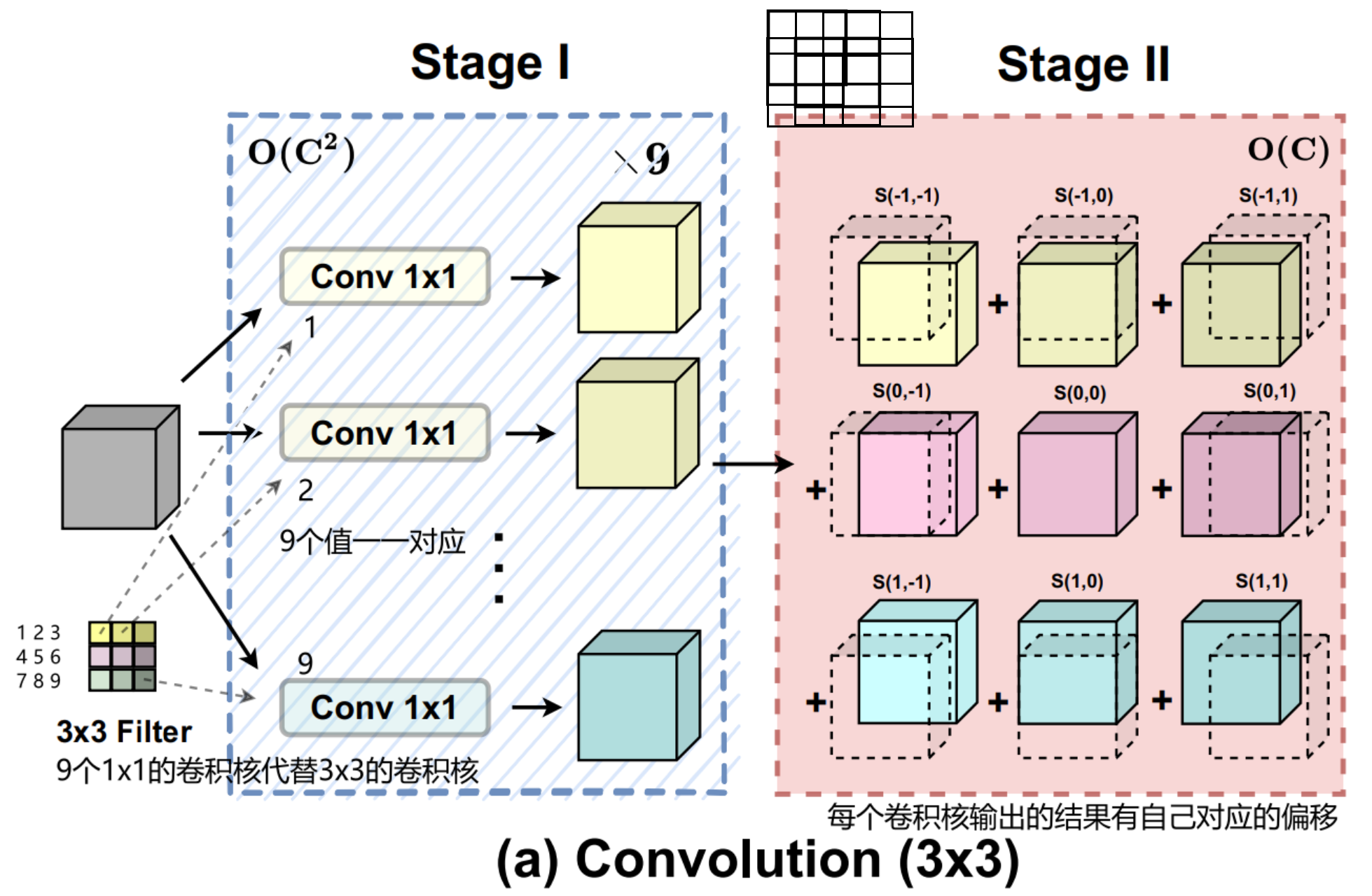
9个1x1的卷积核输出的结果,再拼接起来
例子:4个1x1的卷积核代替1个2x2的卷积核
最左边的3x3正方形为图片特征(这里channel=1)
注意:需要3x3的卷积中pading=1;1x1的卷积中pading=0;这样的话输出结果的形状大小才相同
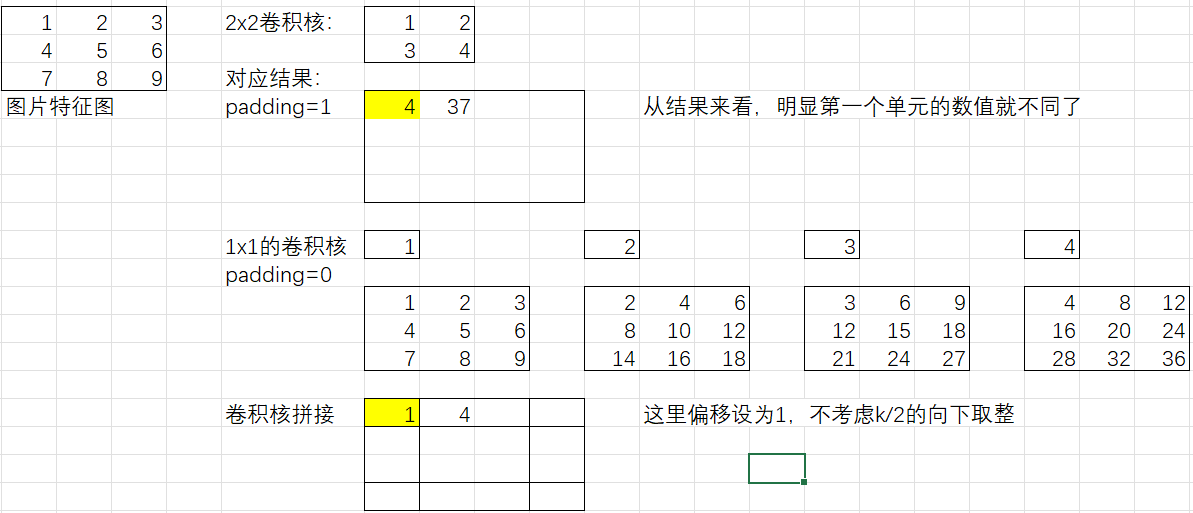
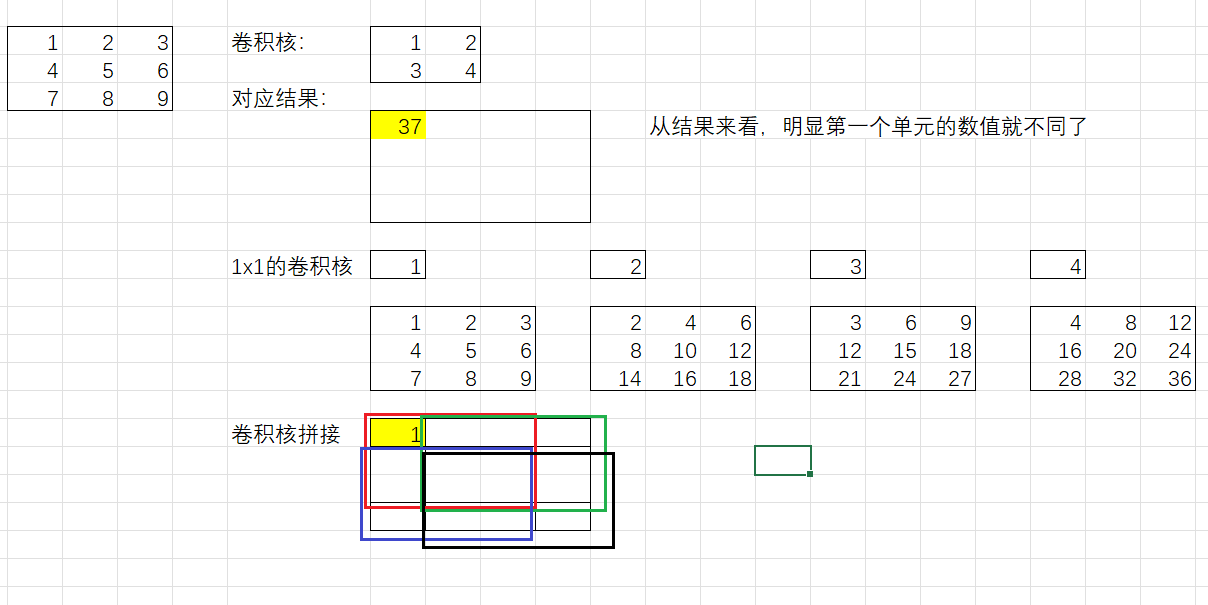
从这里我们可以看出来,其实这种代替的方法得出的数值结果是不相同的,只不过是4个1x1的卷积核模仿了1个2x2的卷积核的学习过程而已。
公式讲述
标准卷积公式

标准公式中的 的讨论?
的讨论?
应该是对Stage2中Conv1输出结果偏移大小的描述
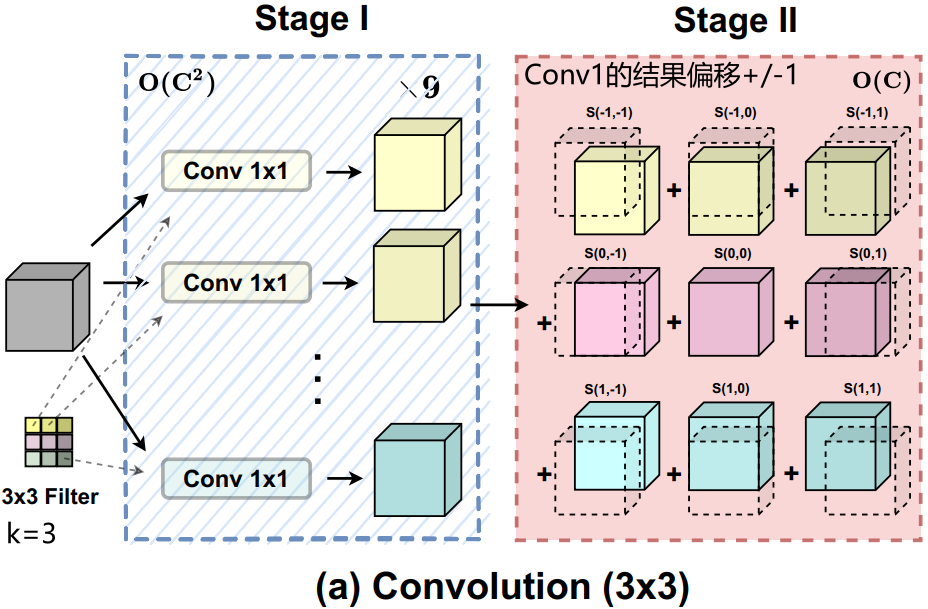
这里k=3,则,所以Conv1的输出结果偏移
重写卷积公式
将上式进行重写
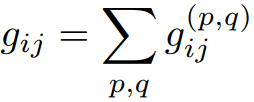
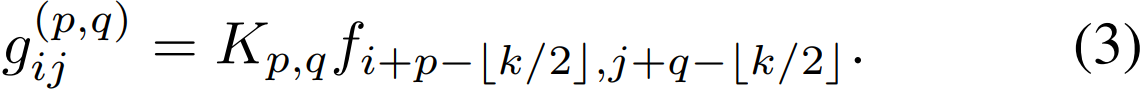
其中为一个卷积核输出的结果
为所有卷积核的结果相加
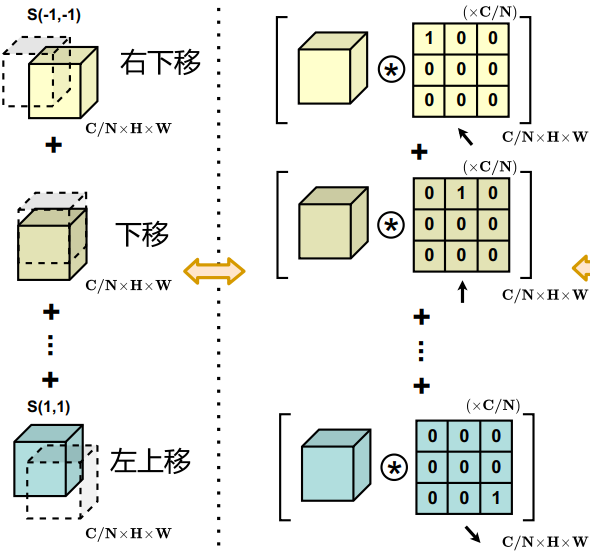
定义Shift操作
将Shift定义为
![]()
定义为:
![]()
其中分别为水平和垂直位移。则等式3可以改写为
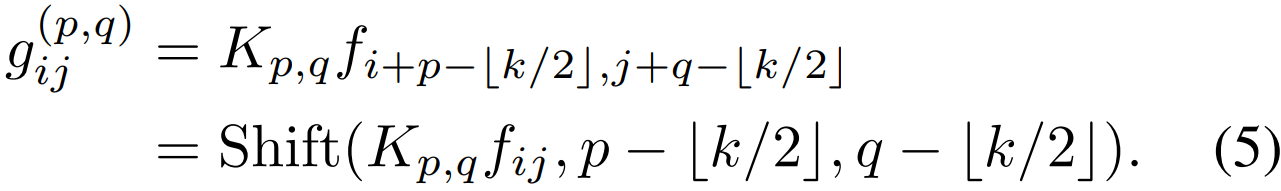
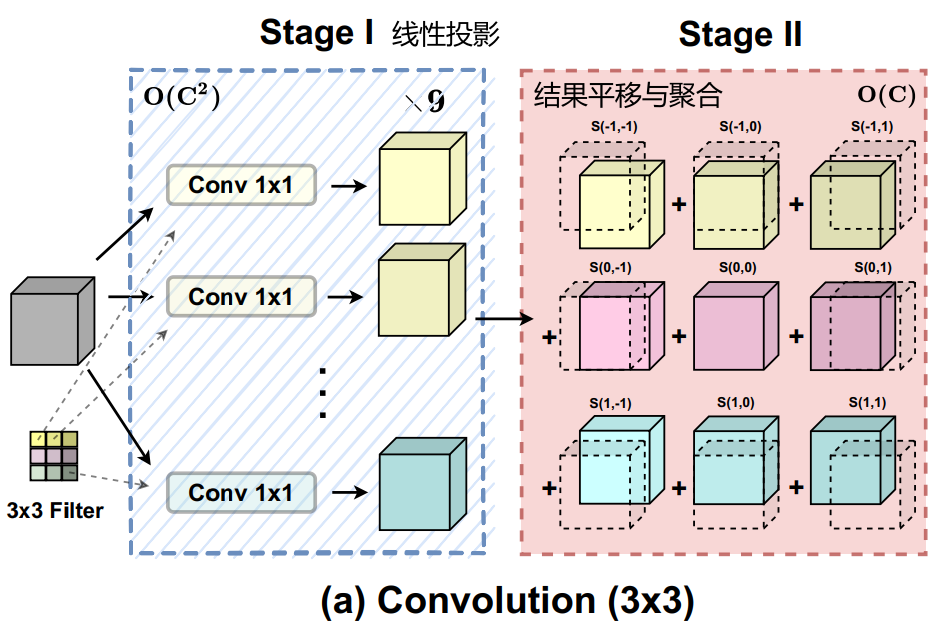
将标准卷积分为两个阶段
第一阶段,将输入的特征图沿某个位置的核权重进行线性投影,即。这与标准的1 × 1卷积相同。
第二阶段,投影后的特征图根据核位置进行平移(所以到底下图用多大的Filter(下图是3x3)得提前定好,因为这个跟每个Conv 1x1得到结果的平移,即与息息相关?不是,这是由
决定的,即),最后聚合在一起。可以很容易地观察到,大部分的计算开销是在1 × 1卷积中进行的,而接下来的移位和聚合是轻量级的。
![]()

3.2. Self-Attention
原理
很简单,这里用一句话来描述:用三个1x1的卷积核得到Q、K、V,之后,由于(a)卷积与(b)self-attention是并行计算的,为了让(b)self-attention赶上(a)卷积,这里只做局部区域的自注意力机制(与swin-transformer有点像,链接:论文解读:SwinTransformer-减少Q、K、V的运算规模-CSDN博客),局部区域对应公式中给出的

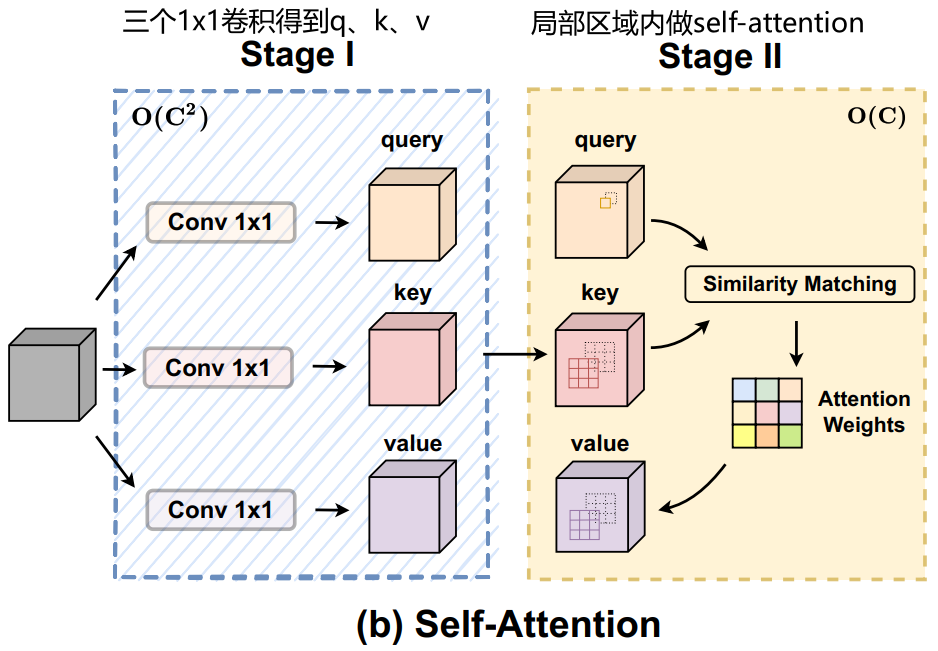
公式解读
这里为一个具有 N 个头的标准自注意力模块。为输入特征图和输出的特征图,其中H,W的图片的大小,输出与输入图片的尺寸保持不变。
分别为F和G对应的像素
的特征张量,则注意力模块的的计算为。
[ 输出特征 = 多个注意力头的相同位置值相加( 注意力权重 × Value ) ]

其中 || 是 N 个注意力头的输出的相同位置值相加(参考文章中说是: N 个注意力头的输出的串联,我觉得有点不对,因为他们是并行得到,串联有种一个头依赖另一个头的感觉)。是queris,keys,values的投影矩阵。
自注意力机制的特点
1:为像素的局部区域,其自注意力机制以
为中心,这说明自注意力机制并非全局的,而是仅在自己
为中心的区域做自注意力机制。
2:是关于
内特征相应的权重。
广泛采用的自我注意模块权重计算如下:
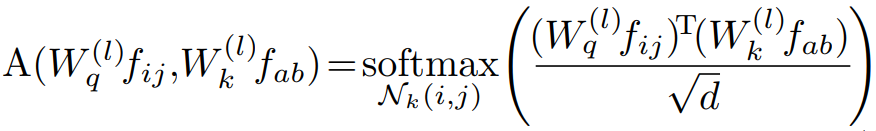
其中d是的特征尺寸。
留意:softmax的作用范围是在这个区域里面的。
将多头注意力机制分成两个阶段


第一阶段类似于传统卷积,进行1×1卷积,将输入特征投影为查询、键和值。
第二阶段包括注意力权重的计算和价值矩阵的聚合,即收集局部特征。
3.3. Computational Cost(比较一、二阶段的计算代价)
为了充分了解卷积和自注意力模块的计算瓶颈,本文分析了每个阶段的浮点运算(FLOPs)和参数数量,并在下表中进行了总结。
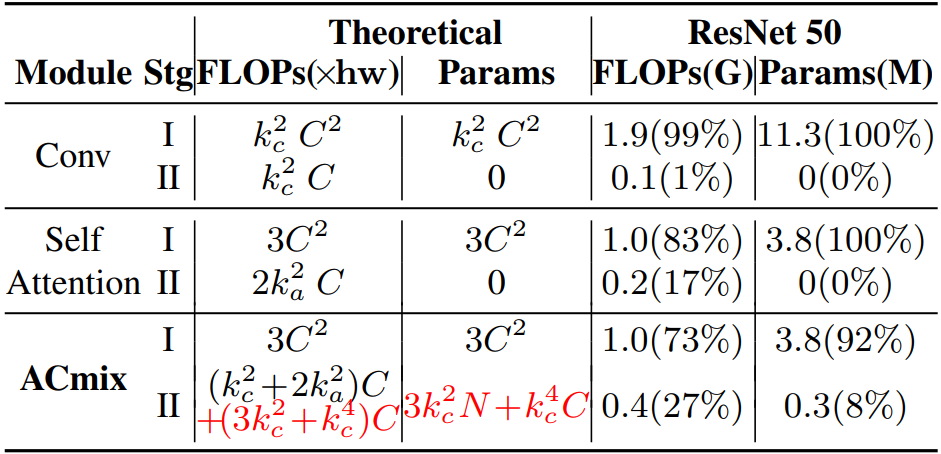
研究表明,中卷积中第一阶段的理论FLOPs 和参数对通道大小C呈二次(即平方)复杂性,而第二阶段的计算成本与C呈一次线性关系。在自注意力模块中也有同样的情况,其中所有的训练参数被保存在阶段I。至于理论得到FLOPs,考虑正常情况下,在ReNET模型中,其中,对于不同的层深度有C=64, 128, 256,512。结果表明,当
时,第一阶段消耗的操作明显大于第二阶段的消耗,并且随着通道大小的增加,差异更明显。
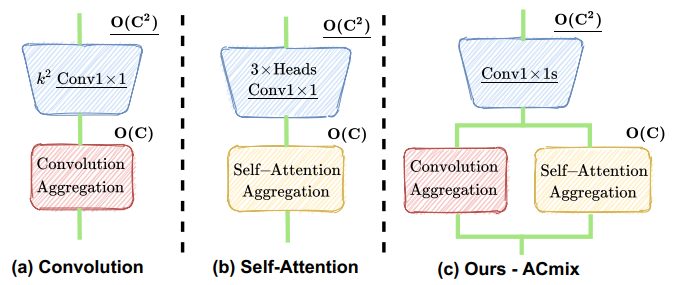
所以随着通道越大,第一阶段的消耗是非常可怕。那么如果我们能够在卷积和自注意力机制中都共享第一阶段,即用同样的一阶段参数,那么将会大大节省计算代价,这便是 4.1. Relating Self-Attention with Convolution 讲的内容。
4. Method
4.1. Relating Self-Attention with Convolution
额,这里说得很抽象...,其实就是上面3.3最后的结论。
自注意力和卷积模块这两个阶段的作用非常相似。第一阶段是特征学习模块,两种方法通过执行1×1卷积来共享相同的操作,从而将特征投影到更深的空间。另一方面,第二阶段对应于特征聚合的过程,尽管他们的学习方法不同。
从计算角度来看,在卷积模块和自注意力模块的第一阶段进行的1×1卷积需要理论的FLOPs和的参数与通道大小C呈2次相关的。相比之下,在第二阶段,两个模块都是轻量级的或几乎没有计算,毕竟只是呈线性关系。
总结:
(1)卷积和自注意力在通过1×1卷积投影输入特征图时实际上共享相同的操作,这能够大大节省计算开销。
(2) 虽然对于捕获语义特征至关重要,但第二阶段的聚合操作是轻量级的,并且不会获得额外的学习参数。
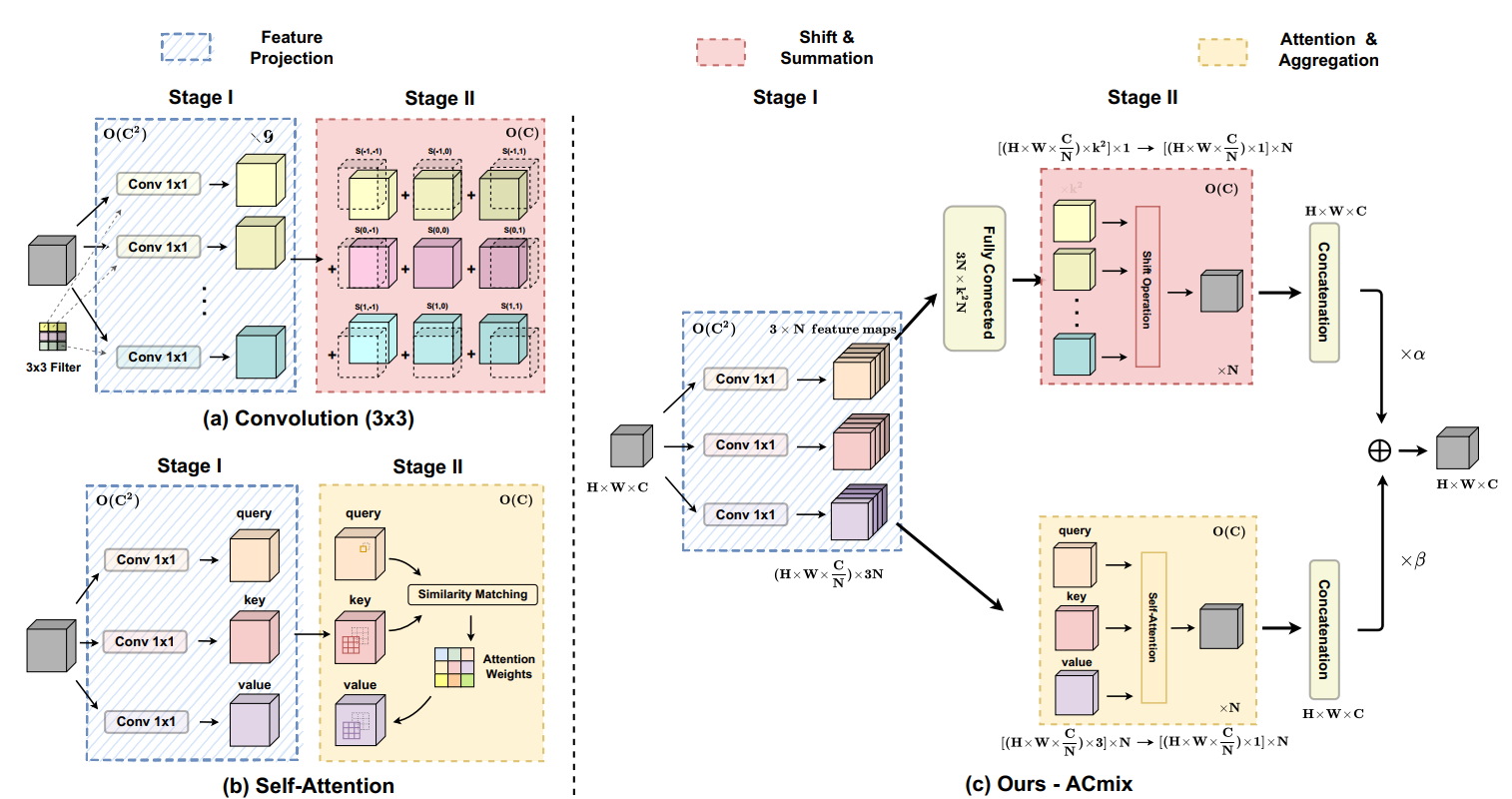
4.2. Integration of Self-Attention and Convolution

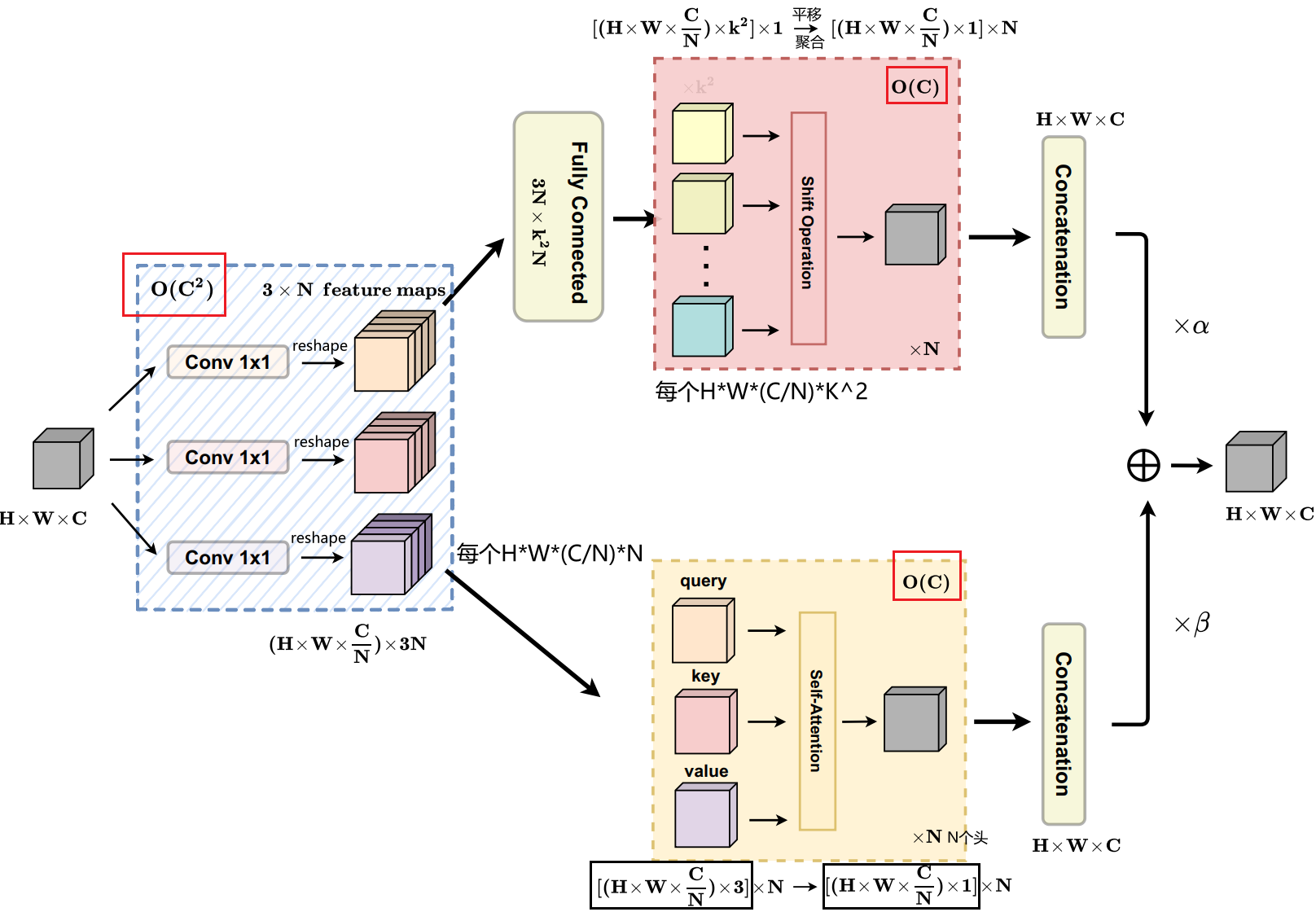
ACmix包括两个阶段。
第一阶段:
输入特征通过三个1×1卷积投影得到3个,之后通过reshape将每个
reshape成,其中N是第二阶段中自注意力机制的头数。
第二阶段:
卷积的stage2在进行偏移之前,先将通过全连接得到
个
,之后偏移聚合得到自注意力机制为N个头分别进行self-attention,每个头的结果
为之后再把N个头拼接起来,得到
。
最后,两条路径的输出相加,其中为可学习参数
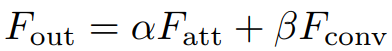
4.3. Improved Shift and Summation
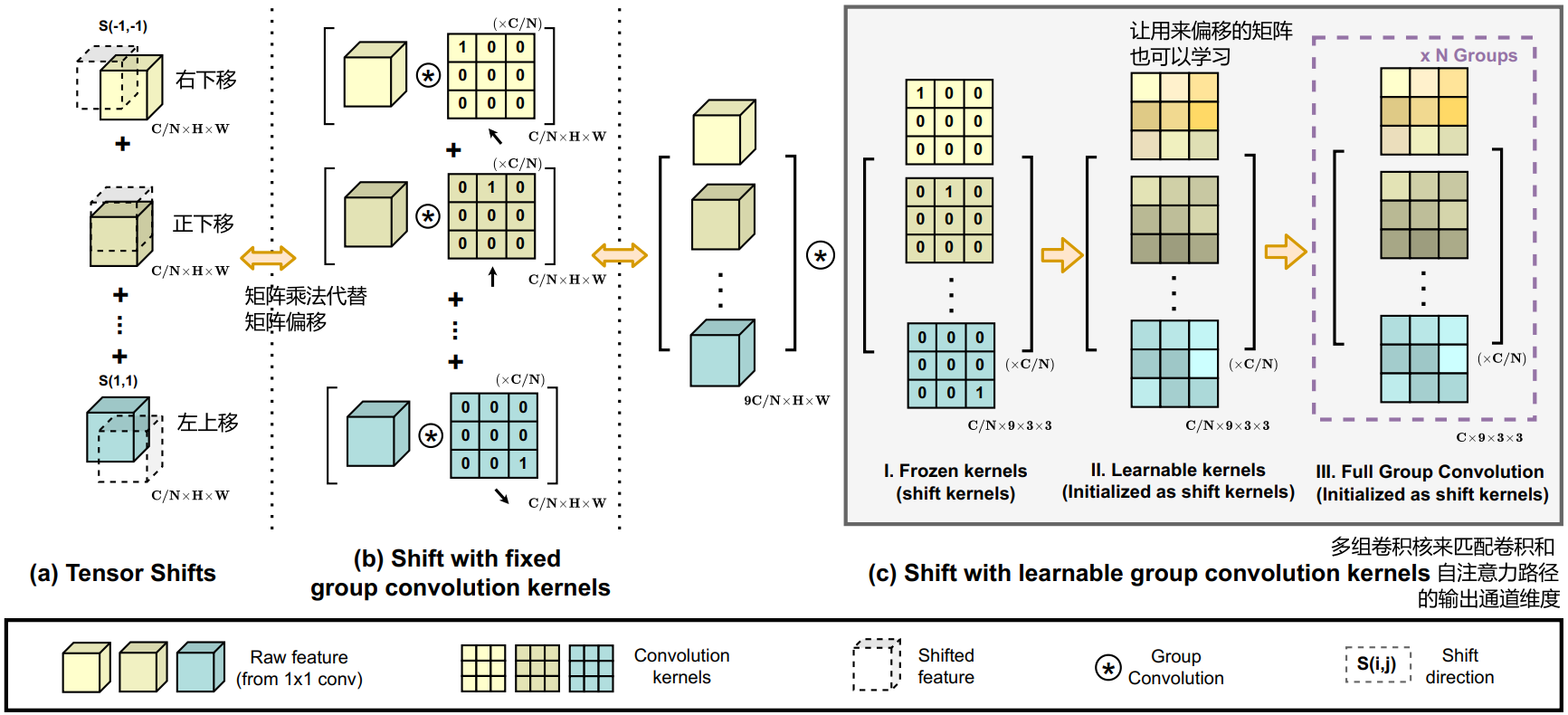
如图4.2节中的图所示,中间特征为卷积路径遵循传统卷积模块中进行的移位和求和操作。尽管理论上它们是轻量级的,但向不同方向移动张量实际上会破坏数据,并且局部性和矢量化难以实现。这可能会大大损害我们的实际效率。
作为补救措施,我们采用固定核的深度卷积来替代低效的卷积张量位移。取Shift(f,−1,−1)
例如,位移特征计算为:
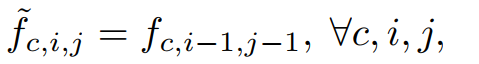
其中c代表输入特性的通道数。
因此,通过针对特定移位方向精心设计的核权重,卷积输出相当于简单的张量移位。为了进一步结合来自不同方向的特征之和,将所有输入特征和卷积核分别连接起来,并将移位运算表示为单组卷积。
在此基础上,作者还引入了一些调整,以增强模块的灵活性。如上图(c.II)所示,将作为偏移使用的卷积核作为可学习的参数,并将移位核作为初始化。这提高了模型容量,同时保持了原始轮流操作的能力。
另外,还使用多组卷积核来匹配卷积和自注意力路径的输出通道维度,如上图(c.III)所示。
一个例子:用矩阵乘法来代替平移

论文里对应的图
4.5. 探索注意力权重
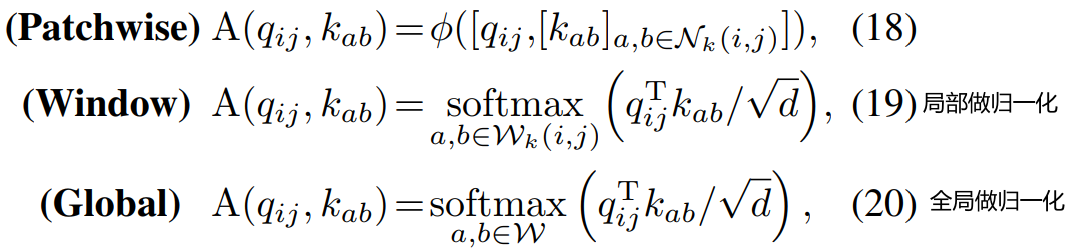
[⋅]表示特征串联,表示两个具有中间非线性激活函数的线性投影层,
表示每个查询标记的专用接收域,W表示整个特征图。然后,计算出的注意力权重可应用于等式(12),并符合一般公式。
5. Experiments
5.1. ImageNet Classification
本篇文章将ACmix应用在4个基本模型当中,包括:ResNet, SAN, PVT and Swin-Transformer,并进行比较。
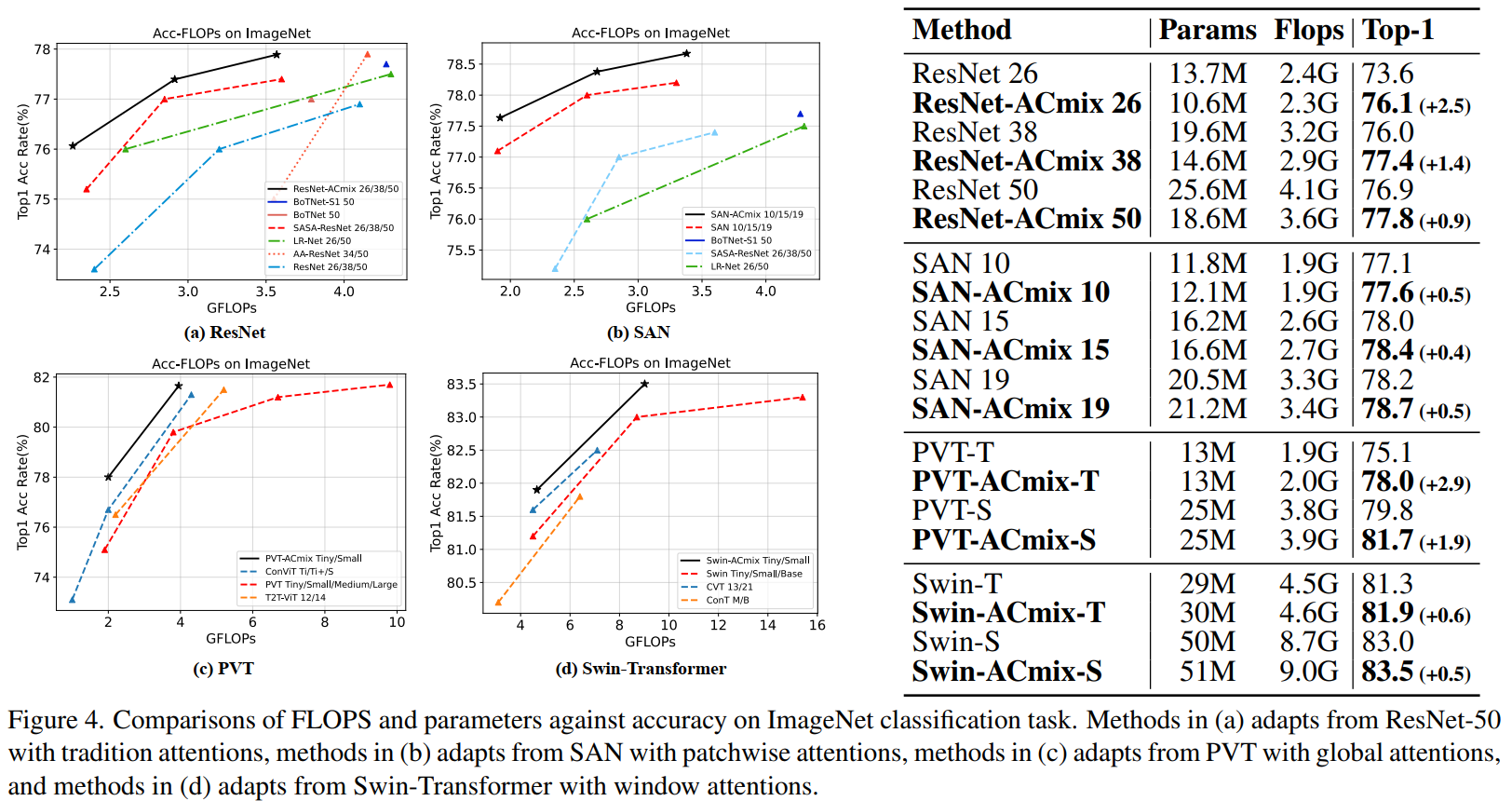
文章还应用在其他下游任务中,这里就不列举了。
参考资料
论文下载
📎论文On the Integration of Self-Attention and Convolution.pdf

代码
GitHub - LeapLabTHU/ACmix: Official repository of ACmix (CVPR2022)
参考文章
On the Integration of Self-Attention and Convolution-CSDN博客
📎On the Integration of Self-Attention and Convolution-CSDN博客 (2023_12_19 16_38_40).html