目录

一.引言

二.树与二叉树简介

1.Tree 树

2.Binary Tree 二叉树

3.Binary Search Tree 二叉搜索树

三.经典算法实战

1.In-Order-Traversal [94]

2.Pre-Order-Traversal [144]

3.Fib [509]

4.N-Tree-Pre-Order-Traversal [589]

5.N-Tree-Post-Order-Traversal [590]

四.总结

---

一.引言

本期我们介绍常用的数据结构树以及其常用的表现形式: 二叉树、二叉搜索树。介绍相关算法前，我们先熟悉下树的结构以及其特点。

二.树与二叉树简介

1.Tree 树

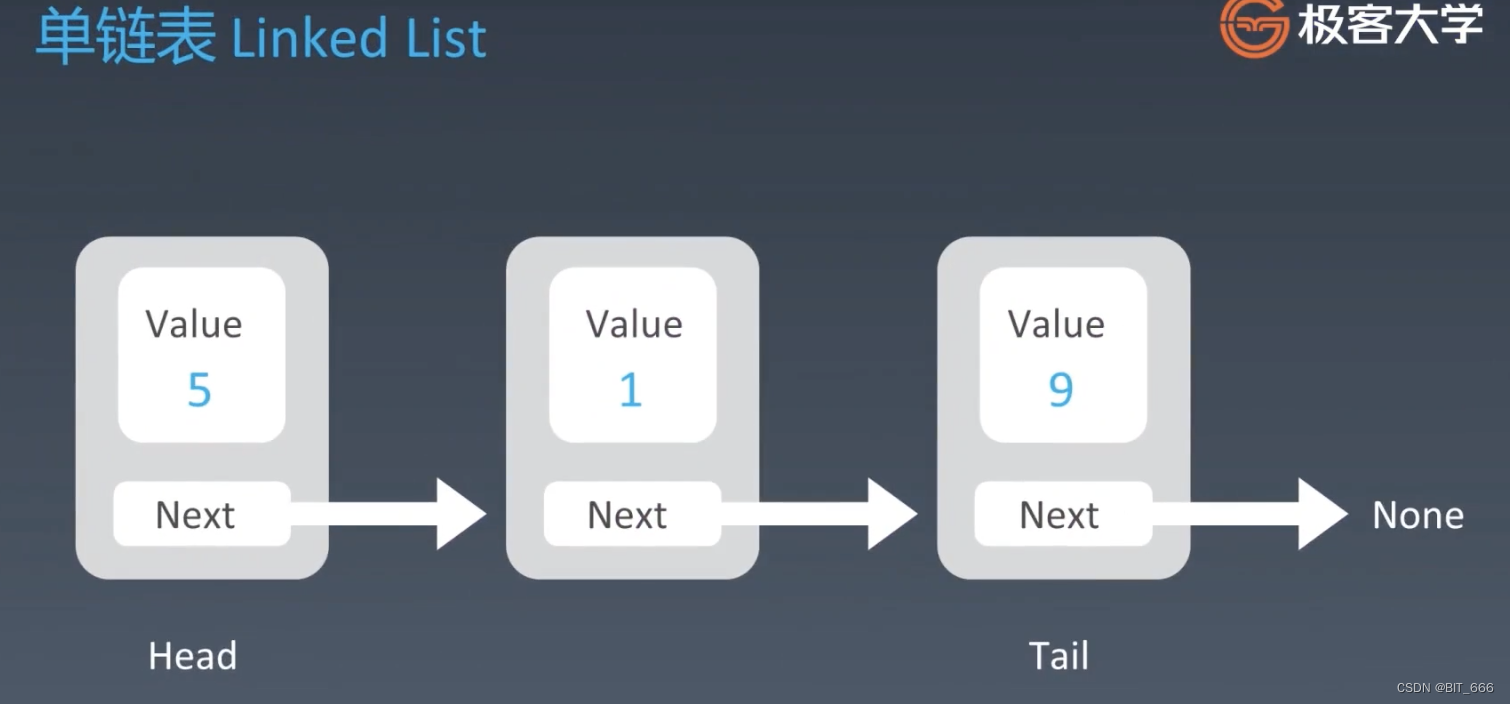
介绍树之前，我们回顾一下之前学习过的数据结构 - LNode 链表，对于每个 Node 而言其只有一个 Next 指针，由此带来的后果是当我们需要遍历链表中某个元素时我们需要 o(n) 的时间复杂度，这个时候出现了跳表，调表通过引入二级、三级、... 多级索引，将数据结构升维，提高其查找元素的时间复杂度。这里 Tree 树的思想就是对一维数据结构的升维，对于某个节点 Node，其 next 指针不在限定为 1 个，而是修改为多个 next 指针，如果是 2 个那就是二叉树、如果是多个那就是多叉树。

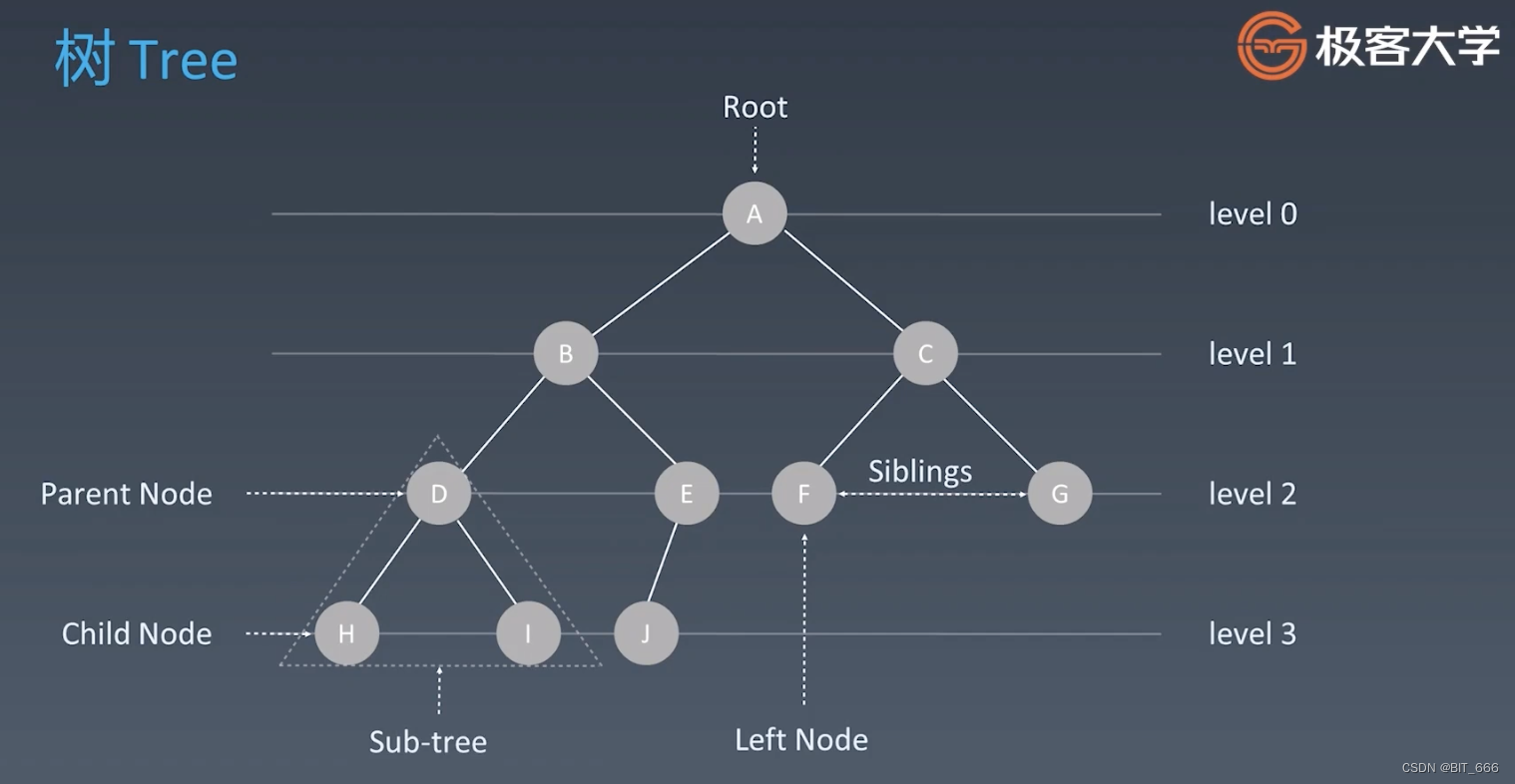
其拥有多个属性:

Root - 根节点，作为整棵树的起始点

Parent/Child Node - 父节点、子节点，例如 D-H 就是父子节点，但 D 又是 B 的子节点

Slidings - 兄弟节点、也可以说姐妹节点，可以理解为一个 Node 下的多个 next 指针，同一级

Sub-Tree - 子树，对于 DHI 构成的子树而言，D 就变成了子树的 root 节点

Level - 层级，树一般是多级结构，不同层又叫树的深度

  

2.Binary Tree 二叉树

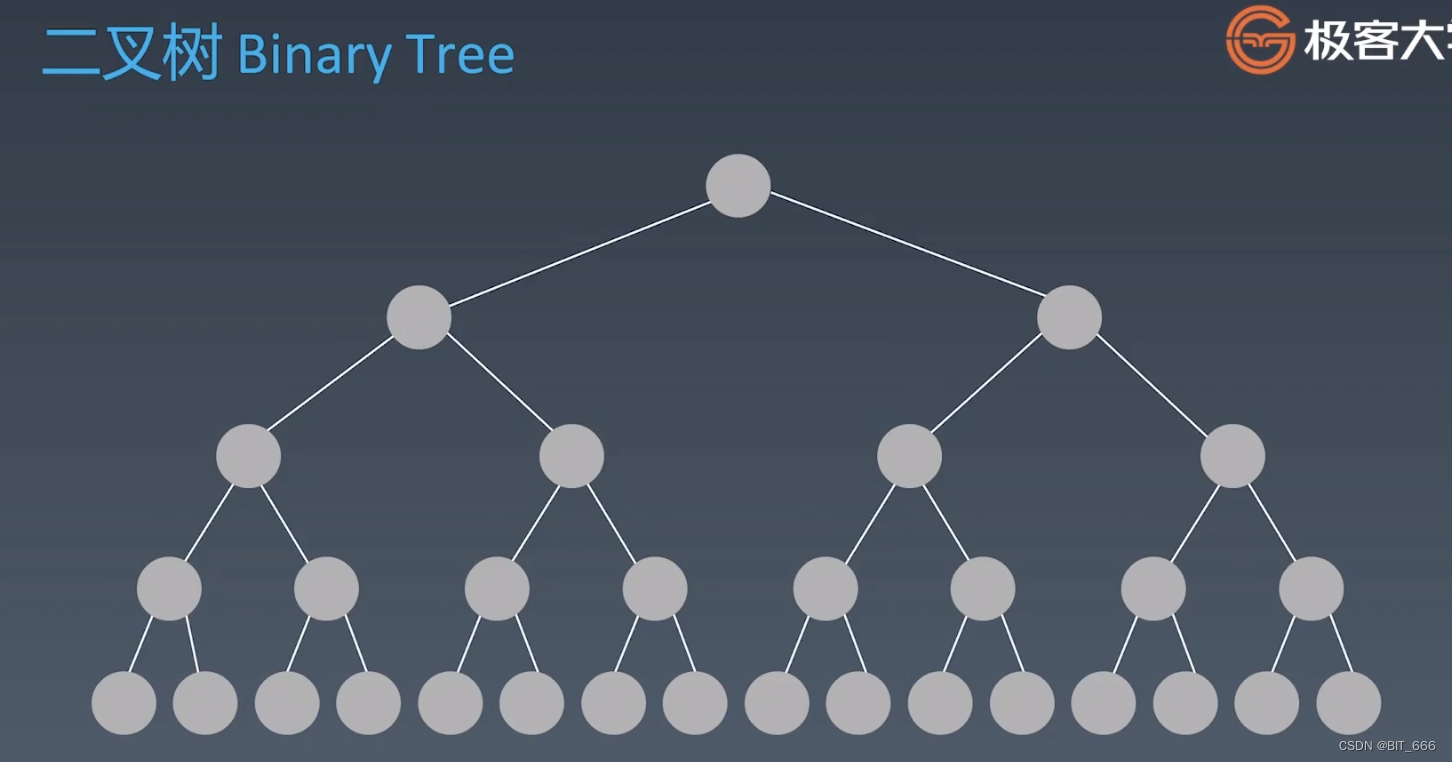
二叉树的儿子节点最多只有两个，即左子结点和右子节点。

◆ 代码实现

◆ 遍历方式

由于树结构的原因，我们不太好使用 For 循环来遍历，除非使用 BFS 或者堆的形式去遍历每一层的数组，基于其 Node 以及 Next 的特点，我们可以通过递归来实现树的遍历。

◆ 遍历代码

下面是 python 的示例代码，其遵循上面遍历的规则:

3.Binary Search Tree 二叉搜索树

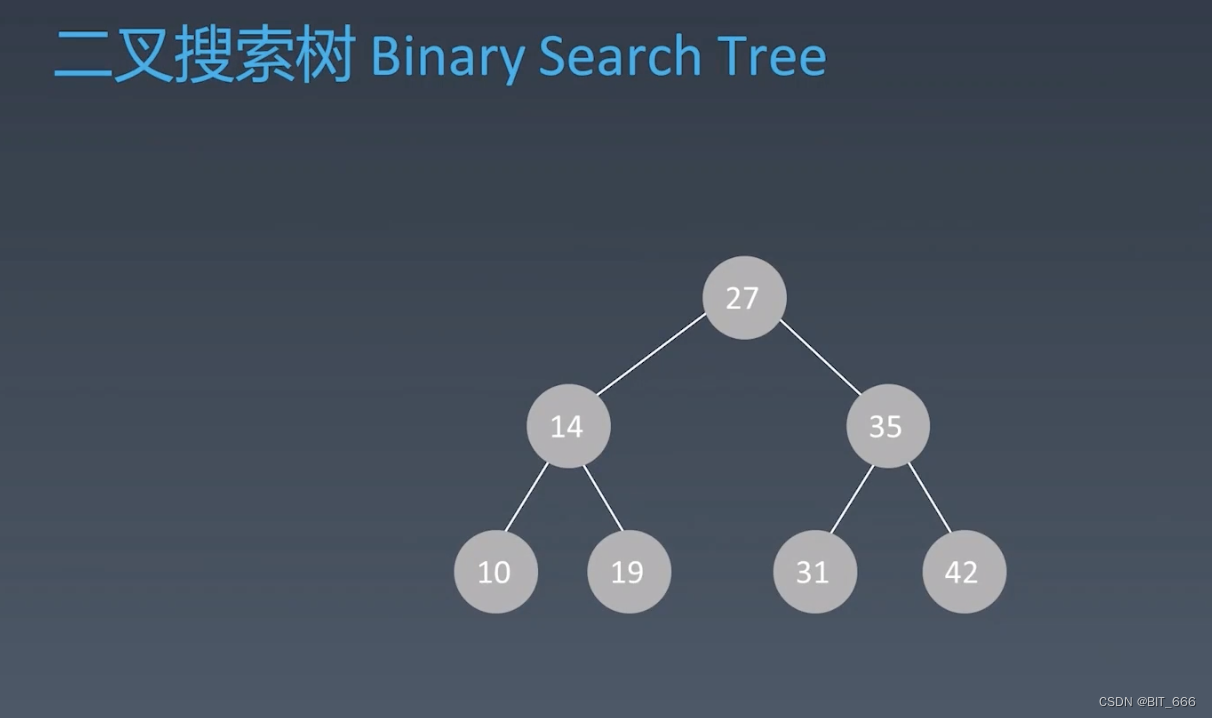
上面提到的二叉树想要查找一个元素依旧需要遍历 o(n) 时间复杂度，因为需要遍历每个节点，这样做其实和链表没有太大区别，为了提高搜索元素的效率，我们可以让二叉树的数据变得更加有序，从而提高搜索效率。 我们将具备如下性质的树称为二叉搜索树:

注意这里中序遍历是 '根左右'，由于左节点都小于根，右节点都大于根，所以二叉搜索树的中序遍历是升序排列。 

二叉搜索树搜索、插入的时间复杂度均为 o(logn)，虽然相比数组 o(1) 的插入复杂度高了一些，但其 o(logn) 的搜索复杂度会比 o(n) 少很多，尤其是当 n 非常的大的时候。

◆ 搜索

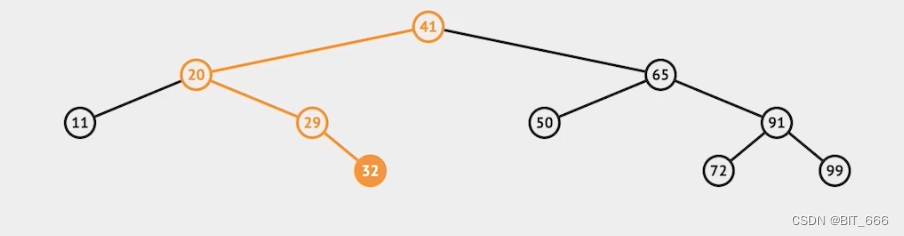
◆ 插入

在上面二叉搜索树的基础上插入 26:

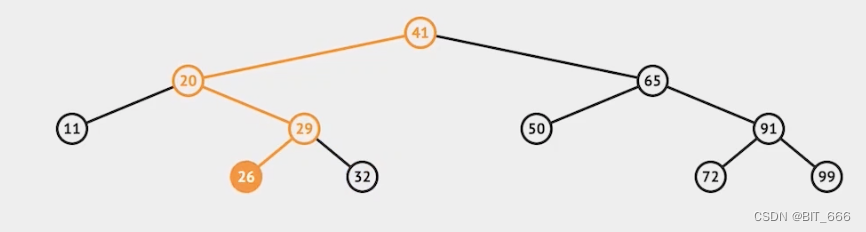
在上面二叉搜索树的基础上插入 55:

◆ 删除 

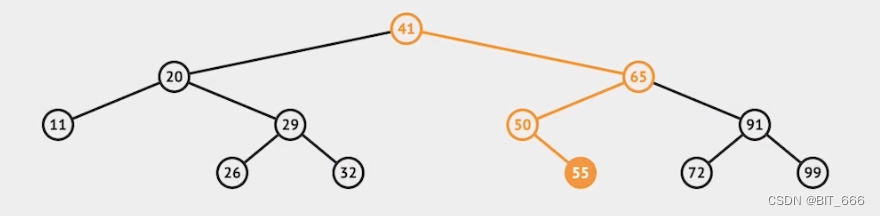
在上面二叉搜索树的基础上删除 32:

在上面二叉搜索树的基础上删除 65:

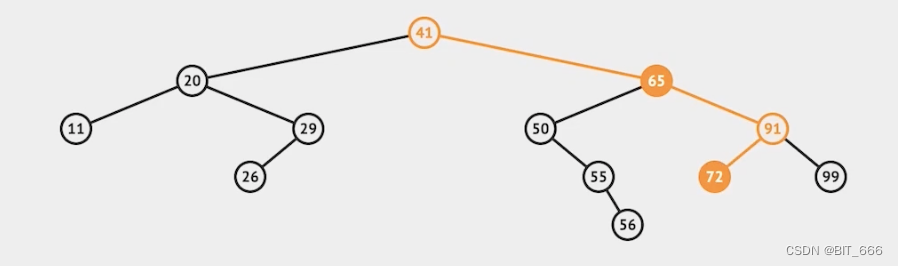
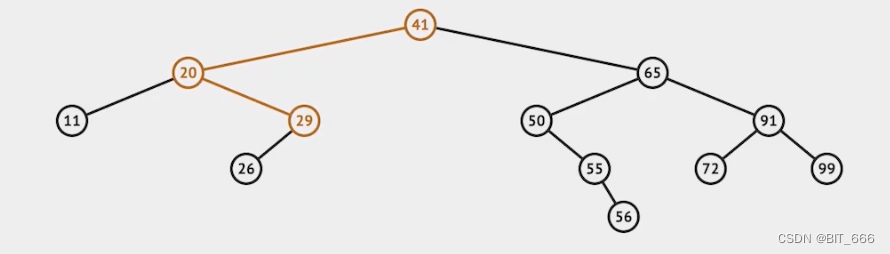
删除叶子节点相对容易，直接删除即可，但是如果删除子树或者树的根节点会涉及到树形态的重构，一般而言，删除树节点一般会选取 Node 的右子树最左边的节点即 72，将 72 替换到 65 的位置并重新调整。

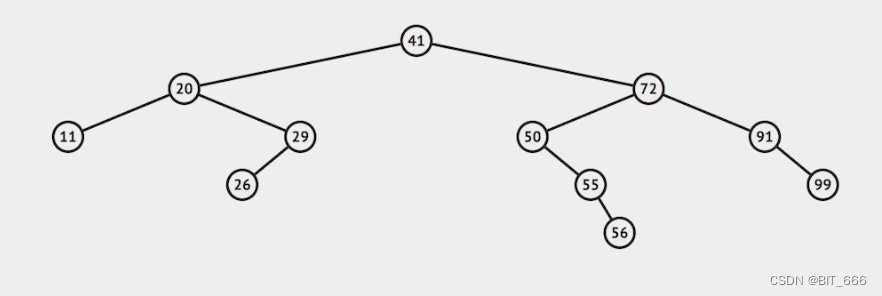
这里继续删除 41 也是同理，我们找到 41 右子树中最左边即最小的节点进行替换即 50:

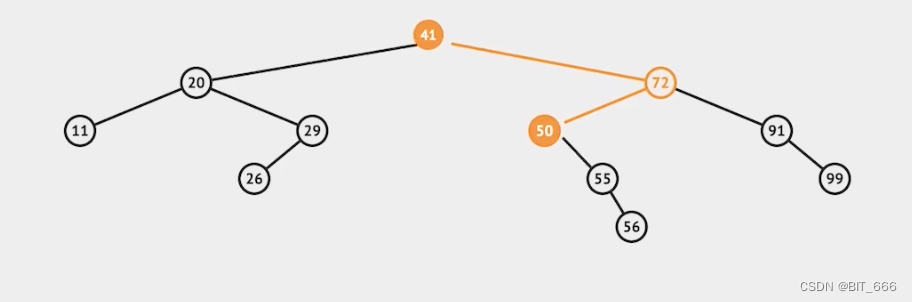
替换后如下状态:

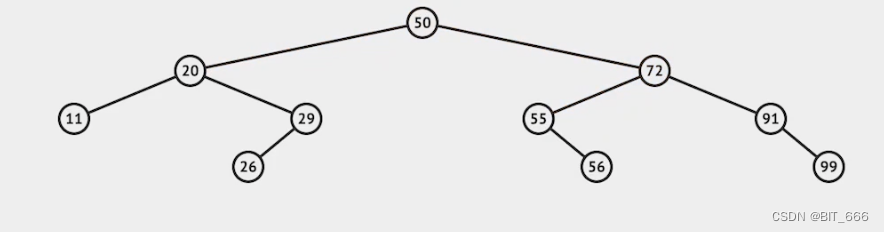
◆ 特殊状态

二叉搜索树添加、删除、查找的时间复杂度均为 o(logn)，特殊情况下退化为 o(n)，下面就是一种典型的特殊情况，其从树结构退化为链表。

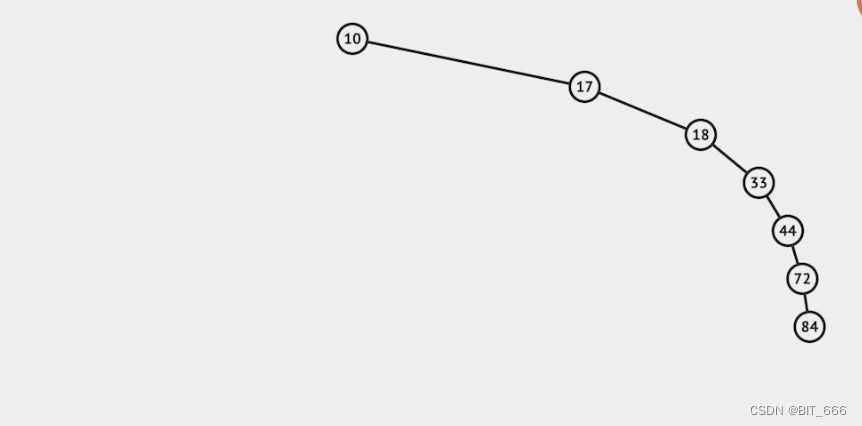
可视化界面: https://visualgo.net/zh/bst

三.经典算法实战

1.In-Order-Traversal [94]

二叉树的中序遍历: https://leetcode.cn/problems/binary-tree-inorder-traversal/

◆ 题目分析

二叉树的前中后序遍历都是很经典的算法，很多同学总是记不清口诀，这里博主分享下自己的记忆方法，不管什么情况下左右都是固定死的，只有根节点 root 是随着遍历方法不同而改变。前序遍历- 根在前，根左右；中序遍历-根在中，左根右；后续遍历-根在后，左右根，所以我们只需要把左中右对应到 root，左右不动即可。

◆ 中序遍历

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution(object):
    def inorderTraversal(self, root):
        """
        :type root: TreeNode
        :rtype: List[int]
        """
        if not root:
            return []
        return self.inorderTraversal(root.left) + [root.val] + self.inorderTraversal(root.right)

直接左根右遍历即可，注意判断 root 为空的条件，如果是前序和后序，只需要更换 [root.val] 的位置即可，这里三种遍历方式是类似的写法。

◆ ​​​​​​​栈实现

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution(object):
    def inorderTraversal(self, root):
        """
        :type root: TreeNode
        :rtype: List[int]
        """
        if not root:
            return []


        # 存储结果 & 栈
        re = []
        stack = []

        cur = root

        # 起始情况 cur 非空 stack 空；后续情况 cur 可能空、栈非空
        while stack or cur:
            # 中序遍历 - 左根右，所以需要找到最左边
            while cur:
                stack.append(cur)
                cur = cur.left
            
            node = stack.pop()
            re.append(node.val)

            if node.right:
                cur = node.right

        return re

上面代码不清晰的同学可以参考下面的示意图，我们通过第二个 while 保证在任何时候都找到最左侧的点， 随后依次弹出，如果右节点非空，则进入右子树。

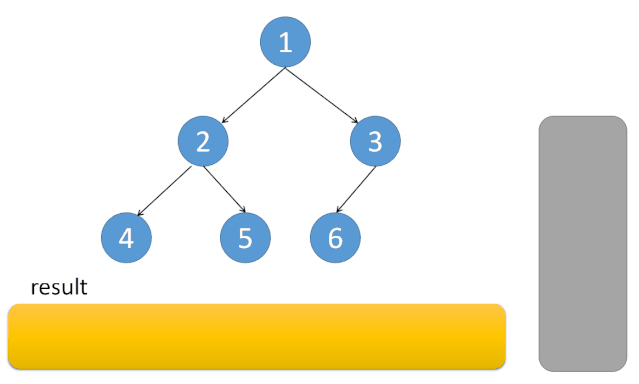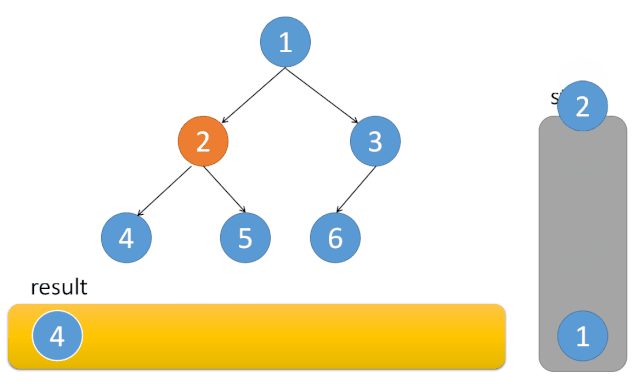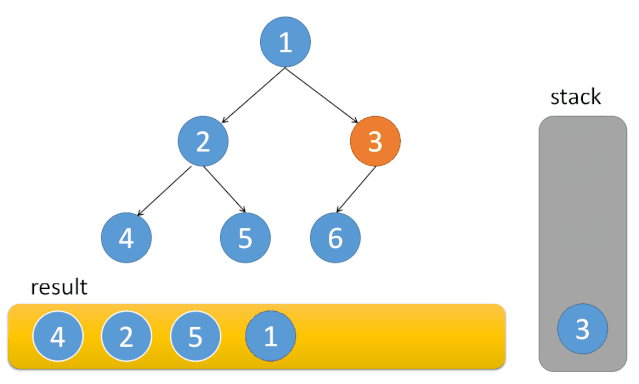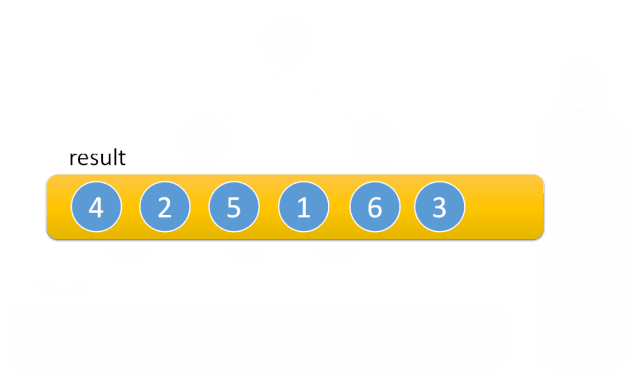
2.Pre-Order-Traversal [144]

前序遍历: https://leetcode-cn.com/problems/binary-tree-preorder-traversal/

◆ ​​​​​​​题目分析

和前面的中序遍历基本类似，这里我们巩固一下，左右不动，动 root，所以前序遍历是 '根左右'。

◆ ​​​​​​​递归实现

class Solution(object):
    def preorderTraversal(self, root):
        """
        :type root: TreeNode
        :rtype: List[int]
        """
        if not root:
            return []

        return [root.val] + self.preorderTraversal(root.left) + self.preorderTraversal(root.right)

这个写法和上面基本相同，下面我们再尝试一种新的写法，我们的递归实际是程序自己生成了一个调用栈，下面我们自己生成栈遍历，顺便复习一下前面的 Stack。 

◆ ​​​​​​​栈实现

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution(object):
    def preorderTraversal(self, root):
        """
        :type root: TreeNode
        :rtype: List[int]
        """

        # 异常判断
        if not root:
            return []
        
        # 存放结果
        res = []

        # 显式维护一个 Stack
        stack = [root]

        # 前序遍历为根左右, 这里栈是先进后出，所以右先进左后进，最后左先出
        while stack:
            node = stack.pop()
            if node:
                res.append(node.val)

                if node.right:
                    stack.append(node.right)
            
                if node.left:
                    stack.append(node.left)
        
        return res
                

3.Fib [509]

斐波那契数列: https://leetcode.cn/problems/fibonacci-number

◆ ​​​​​​​题目分析

斐波那契数列是后项等于前两项之和，即 F(n) = F(n-1) + F(n-1)，这个结构可以看作是一颗 subtree 子树，root 为 F(n)，左右子节点为 F(n-1) 和 F(n-2)，针对 F(n) 我们只需一直向下分叉，找到有多少个叶子节点即可。

◆ ​​​​​​​向下递归

class Solution(object):
    def fib(self, n):
        """
        :type n: int
        :rtype: int
        """
        # 0 和 1 的边界情况，防止越界
        if n == 0:
            return 0
        elif n == 1:
            return 1
        else:
            # 向下递归
            return self.fib(n-1) + self.fib(n-2)

这里可以再简化一下，上面 n=0 return 0、n=1 return 1，可以改成 if n <= 1 return n，这样两行代码就搞定了，不过执行用时有点恼火。 

◆ ​​​​​​​交替前进

class Solution(object):
    def fib(self, n):
        """
        :type n: int
        :rtype: int
        """
        a, b = 0, 1

        # 向右移动
        for i in range(n):
            a , b = b, a+b
        
        return a

这个写法也是基于斐波那契数列的性质进行的，我们只需要维护三元组即可 [a, b, a+b]，然后一直更新 a,b 的指针向右移动，直到我们需要的 n。 

4.N-Tree-Pre-Order-Traversal [589]

N 叉树的前序遍历: https://leetcode-cn.com/problems/n-ary-tree-preorder-traversal/

◆ ​​​​​​​题目分析

二叉树的前序遍历是根左右，固定左右，根在前，多叉树根在前，左右变成了从左到右遍历。

◆ ​​​​​​​前序遍历​​

"""
# Definition for a Node.
class Node(object):
    def __init__(self, val=None, children=None):
        self.val = val
        self.children = children
"""

class Solution(object):
    def preorder(self, root):
        """
        :type root: Node
        :rtype: List[int]
        """
        re = []

        def dfs(node):
            if not node:
                return []
            re.append(node.val)
            for ch in node.children:
                dfs(ch)
        
        dfs(root)
        return re

和下面的多叉树的后序遍历思路一致，就是换了添加 val 的顺序。

5.N-Tree-Post-Order-Traversal [590]

N 叉树的后序遍历: https://leetcode-cn.com/problems/n-ary-tree-postorder-traversal/

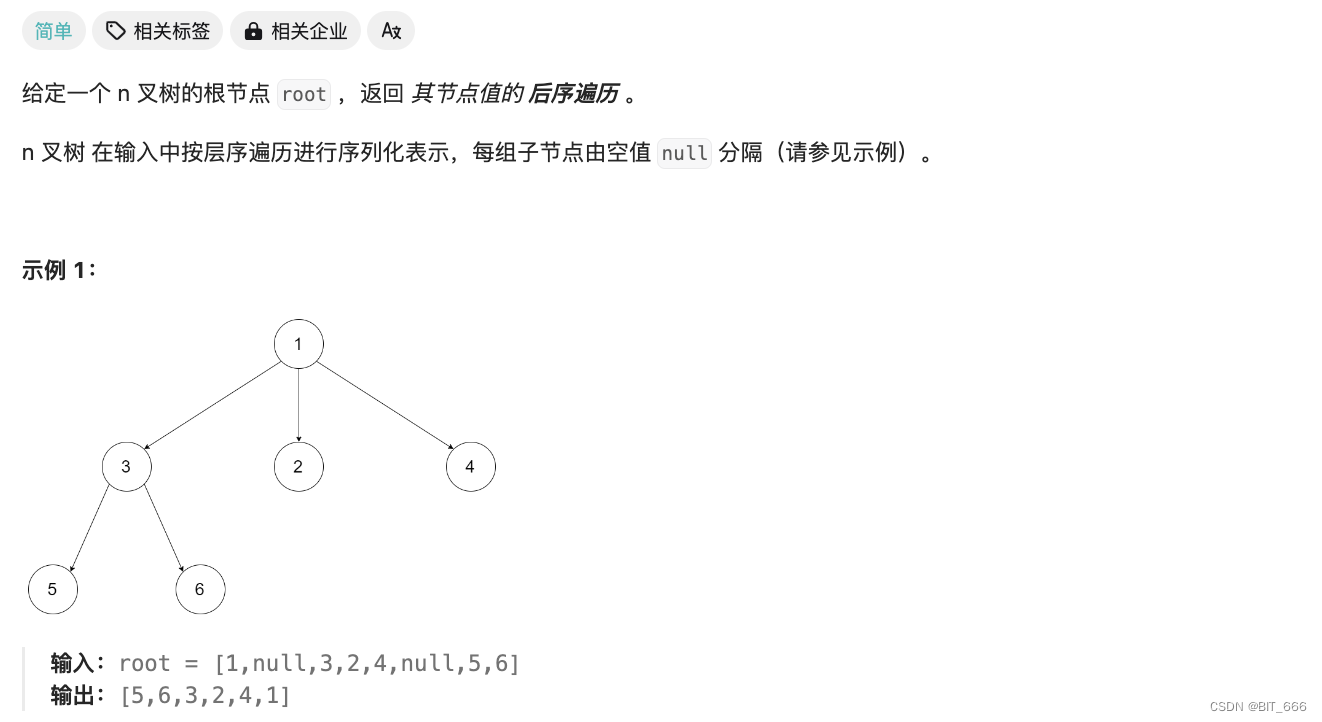
◆ ​​​​​​​题目分析

二叉树后序遍历，固定左右，根放在最后，这里多叉树不止多个叉，但是根依然在最后，所以变成了左 -> 右 + 根，所以增加 for 循环从左到右遍历即可。

◆ ​​​​​​​后序遍历

"""
# Definition for a Node.
class Node(object):
    def __init__(self, val=None, children=None):
        self.val = val
        self.children = children
"""

class Solution(object):

    def postorder(self, root):
        """
        :type root: Node
        :rtype: List[int]
        """

        re = []

        def dfs(node):
            if not node:
                return []
            # 左右根，这里左右变多了，但是从左到右的顺序不变，左->右，再根
            for ch in node.children:
                dfs(ch)
            re.append(node.val)
        
        dfs(root)
        return re


        
        

四.总结

上面讲解了 Tree 树、Binary Tree 二叉树以及 Any Tree 多叉树的基本概念以及 LeetCode 里一些基本的算法操作，主要了解了树的结构特点，严格意义上说，栈是特殊的树，二叉树是特殊的多叉树。本节的题目中我们着重掌握递归的思想，因为树的结构不好显式的进行遍历，其次由于递归内部采用 Stack 实现，因此最好也要掌握手动栈实现树的遍历。最好感慨一下这些题目经常做，但是经常忘，就像赵本山测试范伟智商似的，只能答老题，而且老题稍微一变花样就又被忽悠了，哎...多多练习吧，啥时候练得过拟合就好了。