🌈武汉大学惯性导航课程合集是入门惯导的精品课程~ 作为导航路上的鼠鼠我,要开始学习惯性导航了~ 需要达到的要求是大致了解惯导的原理等~ 后期会陆续更新惯导相关的知识和笔记等~
🐬 本blog为 武汉大学惯性导航课程 的记录~ 感谢团队提供的开源课件ppt和相关代码~
☘️概览:惯性器件的误差和标定(下)
⭐️省流:1️⃣介绍加速度计和陀螺仪的测量模型(包括零偏误差 交轴耦合误差等);2️⃣一些常用的误差模型和识别方法(解决用什么模型把这些误差识别出来,你得到的一系列误差用什么模型得到,怎么进行分析 ~ )3️⃣IMU误差的标定(两位置法 六位置法)
🍭这门课程讲的真的很好,墙裂建议惯导新手入门 加油加油~ (●ˇ∀ˇ●)
🌴这篇文章简要介绍了一下惯导~ 我觉得写的不错~ 大家可以看看形成一个大体的认识
惯性器件的误差和标定(下)
文章目录
- 惯性器件的误差和标定(下)
- 测量模型
- 陀螺测量模型
- 陀螺测量模型
- 术语解释
- 误差模型
- 误差模型的识别和参数确定方法
- 自相关分析(通用)
- 功率谱密度分析(通用)
- Allan方差分析(适用于惯导)
- 测试和标定
- IMU标定
- 重要性
- 参考源,方法,设备
- 加速度两位置法———静态标定(对于单轴)
- 加速度六位置法———静态标定(对于单轴)
- 陀螺两位置法———静态标定(对于单轴)
- 标定总结
测量模型
陀螺测量模型
都是三维向量
ω
~
=
ω
+
b
ω
+
S
ω
+
N
ω
+
ε
ω
\widetilde{\boldsymbol{\omega}}=\boldsymbol{\omega}+\boldsymbol{b}_\omega+\mathbf{S}\boldsymbol{\omega}+\mathbf{N}\boldsymbol{\omega}+\boldsymbol{\varepsilon}_\omega
ω
=ω+bω+Sω+Nω+εω
ω
~
:
\tilde{\omega}:
ω~: 测量值 (deg/hr)
ω \omega ω : 真实的角速度(deg/hr)
b ω : {b}_\omega: bω: 陀螺零偏 (deg/hr)
S S S : 陀螺比例因子误差矩阵
N N N : 陀螺交轴耦合误差矩阵
ε
ω
\varepsilon_{\omega}
εω : 陀螺传感器噪声矢量 (deg/hr) 3x1的标量
b
ω
=
[
b
ω
,
x
b
ω
,
y
b
ω
,
z
]
S
=
[
s
x
0
0
0
s
y
0
0
0
s
z
]
N
=
[
0
γ
x
y
γ
x
z
γ
y
x
0
γ
y
z
γ
z
x
γ
z
y
0
]
\boldsymbol{b}_\omega=\begin{bmatrix}b_{\omega,x}\\b_{\omega,y}\\b_{\omega,z}\end{bmatrix}\quad\mathbf{S}=\begin{bmatrix}s_x&0&0\\0&s_y&0\\0&0&s_z\end{bmatrix}\quad\mathbf{N}=\begin{bmatrix}0&\gamma_{xy}&\gamma_{xz}\\\gamma_{yx}&0&\gamma_{yz}\\\gamma_{zx}&\gamma_{zy}&0\end{bmatrix}
bω=
bω,xbω,ybω,z
S=
sx000sy000sz
N=
0γyxγzxγxy0γzyγxzγyz0
比例因子:主轴的误差–主对角线
交轴耦合:交叉项
🍎交叉耦合系数(cross coupling coefficient)是指沿加速度计的输入轴及其垂直方向都有加速度作用时,加速度计的输出中有一项与这两个加速度的乘积成比例系数。
所以这两者可以合并成一个矩阵
没有考虑非线性误差等
陀螺测量模型
f ~ = f + b f + S 1 f + S 2 f 2 + N f + δ g + ε f \widetilde{\boldsymbol{f}}=\boldsymbol{f}+\boldsymbol{b}_f+\mathbf{S}_1\boldsymbol{f}+\mathbf{S}_2\boldsymbol{f}^2+\mathbf{N}\boldsymbol{f}+\delta\boldsymbol{g}+\boldsymbol{\varepsilon}_f f =f+bf+S1f+S2f2+Nf+δg+εf
f ~ \tilde{\boldsymbol{f}} f~ :测量值 (m/sec2)
f {\boldsymbol{f}} f :真实比力 (m/sec2)
b f : \boldsymbol{b}_f: bf:加速度计零偏 (m/sec 2 ) ^2) 2)
S 2 : \mathbf{S}_2: S2:非线性比例因子误差矩阵N :交轴耦合矩阵
δ g : \delta\boldsymbol{g}: δg: 重力异常
(其实不是传感器的误差,客观上的,比如磁场,有个矿,用这个加速度计来补偿,帮重力模型背锅的;这样就可以方便一些~ 方便建模 几十ug )
中低精度的惯导一般感知不出来
ε f : \varepsilon_f: εf:加速度计传感器噪声矢量 (m/sec2)
考虑了非线性误差等
术语解释
🎈 需要联系上下文判断一些术语,同时要对这些术语理解透彻。可以标注不同的统计参量,比如RMS(方均根) P-P(峰峰值 ) ±(最大最小值)等
🍐易混淆的概念:
Bias vs. Bias error; SF vs. SF error;
Random Walk vs. White Noise
这些可能都认为一样 需要联系上下文
🍒同义词:
Drift, variation, instability, stability; 指 陀螺零偏
Non-orthogonality, cross-axis, axis-misalignment 指交轴耦合
🍅易混淆的单位:
Accel: m/s2, g, mg, ug, mGal, m/s/h;
Gyro:rad/s, deg/s, deg/h;
For white noise (or random walk):
Spectrum density (q) vs. sqrt(q)
rad/s/sqrt(Hz), deg/s/sqrt(Hz) = deg/sqrt(s), deg/sqrt(h);
m/s2/sqrt(Hz) = m/s/sqrt(s), ug/sqrt(Hz), m/s/sqrt(h).
误差模型

一阶高斯马尔科夫过程 :变化快慢和幅度都可以通过参数来调整
随机游走:一个参数就能调整 (但是比较粗糙)
误差模型的识别和参数确定方法
解决用什么模型把这些误差识别出来,你得到的一系列误差用什么模型得到,怎么进行分析~
自相关分析(通用)
画出自相关函数
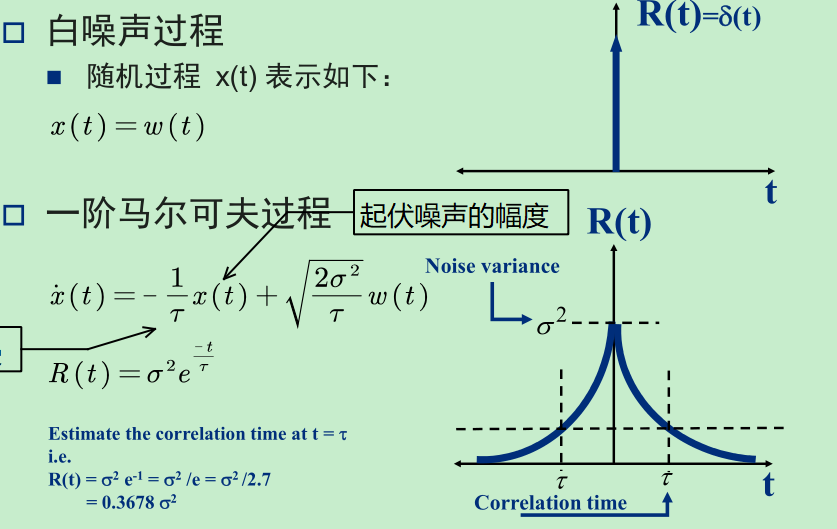
对于一阶马尔可夫过程 τ (相关时间) → 0 就退化成白噪声
功率谱密度分析(通用)
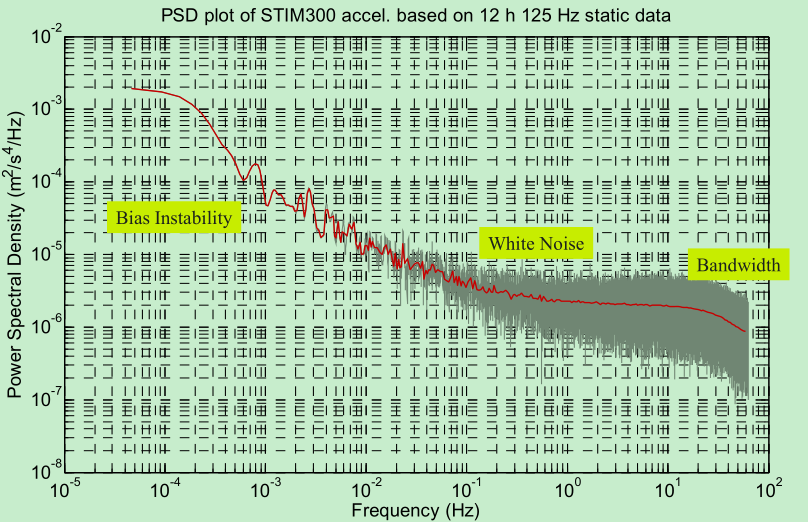
可以从图中看到功率谱密度 带宽 零偏不稳定性等。
Allan方差分析(适用于惯导)
🌿前两种方法适合分析中高频段~ 不适合分析低频段,我们惯导关心的主要是是低频段

1️⃣分块;(不同的时间尺度 比如5min一次 10min一次)
2️⃣求平均值;
3️⃣相邻块的平均值求差;(把不关心的,长时间的不确定性去掉)
4️⃣求这些块的RMS值;
Allen方差曲线:不同尺度上的误差序列的不确定性的大小
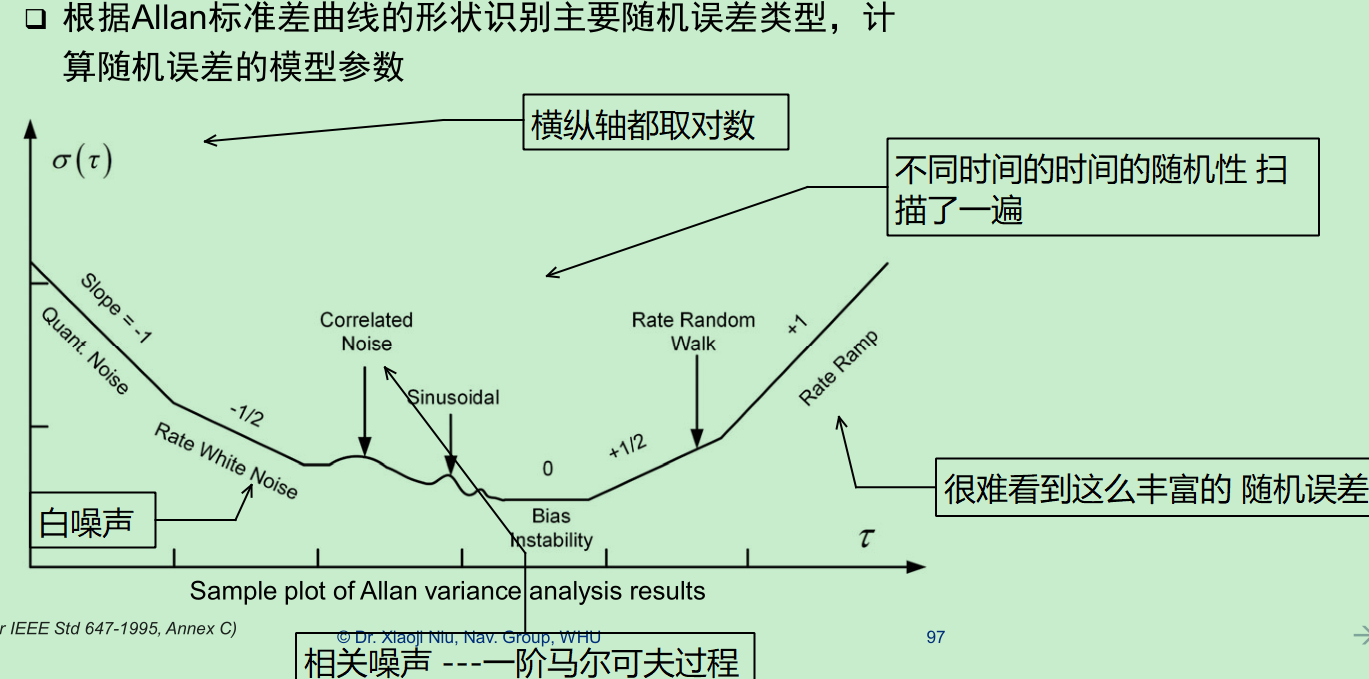
可以看到不同的随机模型———参数提取
但是现实中,很难看到这么丰富的 随机误差 ,只能看到几个主要的矛盾~
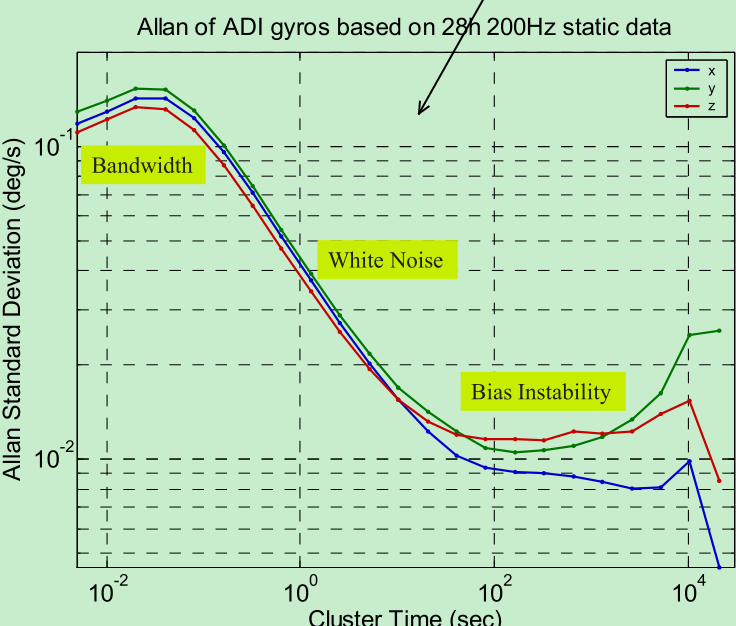
测试和标定
测试: 相当于最终的考核 (期末考试)
标定:把能去掉的误差 (一般是系统误差,比如常值误差)扣掉 相当于补偿 (相当于考前答疑)
标定是将仪器输出与已知的参考信息并确定系数强制输出与参考信息一致输出值范围的过程。
把传感器里面的主要的系统误差去除掉

标定:一般是恒定的值,然后后面可以把误差补偿~
所有系统误差都可以得到补偿。但只考虑主要的误差。一些随机误差可以通过导航算法和在线补偿。
IMU标定
标定是将仪器输出与已知的参考信息并确定系数强制输出与参考信息一致输出值范围的过程。
把传感器里面的主要的系统误差去除掉
重要性
🌱标定可去除系统性误差
δ
r
N
=
δ
r
N
,
0
+
δ
v
N
,
0
⋅
t
+
1
2
(
g
⋅
δ
θ
0
+
b
a
N
)
t
2
+
1
6
(
g
⋅
b
g
E
)
t
3
\begin{equation}\delta r_N=\delta r_{N,0}+\delta v_{N,0}\cdot t+\frac12(g\cdot\delta\theta_0+{b_{aN}})t^2+\frac16(g\cdot{b_{gE}})t^3\end{equation}
δrN=δrN,0+δvN,0⋅t+21(g⋅δθ0+baN)t2+61(g⋅bgE)t3
⚙️ 加速度计零偏的影响
1️⃣初始横滚角和俯仰角
2️⃣速度和位置
⚙️ 陀螺零偏的影响
1️⃣航向角
2️⃣姿态 速度和位置
参考源,方法,设备
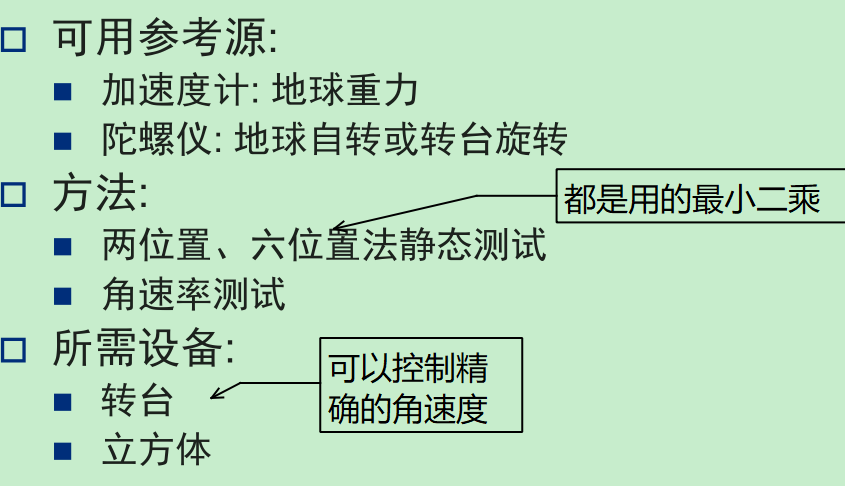
加速度两位置法———静态标定(对于单轴)
传感器的敏感轴朝着哪,就规定正方向在哪
左图:f=a-g 由于重力加速度是向下的,和正方向相反,所以是一个负的值,而本身前面有一个负号,所以就变成了正的值了。

通过两位置标定,可以测出零偏和比例因子
噪声被求平均(滤波)滤除了 ,可以忽略
具有鲁棒性

加速度六位置法———静态标定(对于单轴)
加速度计也要同时记录其他的位置~可以用立方体进行标定
交轴耦合系数(cross coupling coefficient)是指沿加速度计的输入轴及其垂直方向都有加速度作用时,加速度计的输出中有一项与这两个加速度的乘积成比例系数。

六位置的加速度计输出模型可以写作如下矩阵形式
[
f
ˇ
1
f
ˇ
2
f
ˇ
3
f
ˇ
4
f
ˇ
5
f
ˇ
6
]
=
M
[
f
1
f
2
f
3
f
4
f
5
f
6
1
1
1
1
1
1
]
\begin{equation}\begin{bmatrix}\check{\boldsymbol{f}}_1&\check{\boldsymbol{f}}_2&\check{\boldsymbol{f}}_3&\check{\boldsymbol{f}}_4&\check{\boldsymbol{f}}_5&\check{\boldsymbol{f}}_6\end{bmatrix}=\mathbf{M}\begin{bmatrix}f_1&f_2&f_3&f_4&f_5&f_6\\1&1&1&1&1&1\end{bmatrix}\end{equation}
[fˇ1fˇ2fˇ3fˇ4fˇ5fˇ6]=M[f11f21f31f41f51f61]
记作: L = M A 记作:\begin{equation}\mathbf{L}=\mathbf{M}\mathbf{A}\end{equation} 记作:L=MA
M矩阵中中包含12个待估参数,共有18个(6个位置xyz三个轴三次)方程。可用最小二乘法求解M
M
^
=
L
A
T
(
A
A
T
)
−
1
\begin{equation}\hat{\mathbf{M}}=\mathbf{L}\mathbf{A}^\mathrm{T}\left(\mathbf{A}\mathbf{A}^\mathrm{T}\right)^{-1}\end{equation}
M^=LAT(AAT)−1
🌾 12位置标定法
旋转一定角度(比如180°)再测一次,然后再取平均值。消除因为地不平的误差。
陀螺两位置法———静态标定(对于单轴)

不要忽略地球自转
出于工程化的原因,一般不用角速度转台(角速度精确控制)(太贵了),用角位置转台,(角度精度很好保障~)只要相对转角
对角速度时间积分得到相对转角 和转台的比对
陀螺输出一个角速度,做时间积分得到转角和转台旋转的角度进行对比
六位置法 陀螺标定比较复杂,因为有地球的自转的影响,除非知道航向角。零偏和比例因子可以知道,但是交轴耦合比较模糊。
标定总结
标定的精度依赖于各轴相对于参考坐标对准的准确性。
为了获得准确的标定结果,需要一些专业设备(如转台或规则的立方体)来获得IMU的精确姿态和旋转角。
由于对专业设备的依赖性,这些标定方法主要设计用于实验室测试、厂家校准和对较高精度的IMU的标定。
系统级的标定
不需要专业设备
使用间接的参考
用于低端传感器
现场的标定和维护

🌈ok,完结~点个赞 (●ˇ∀ˇ●)点个赞 (●ˇ∀ˇ●)


![[Angular] 笔记 3:ngIf](https://img-blog.csdnimg.cn/direct/396796d0f17b44e4a2796dfcaad152c7.png)