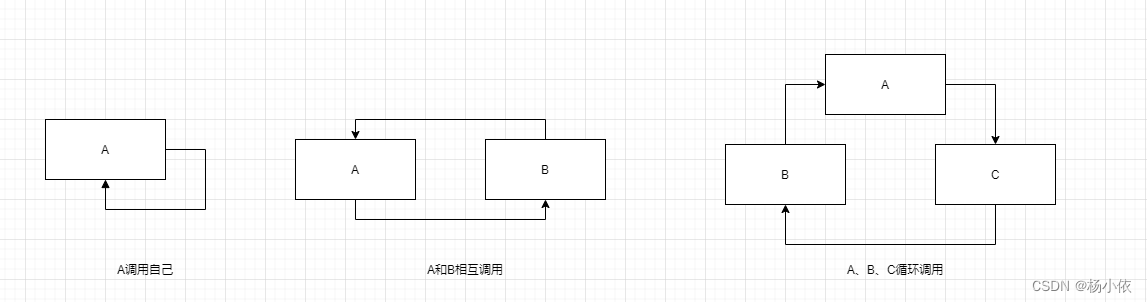
一、引言
前面我详细介绍了如何绘制漂亮的折线图和柱状图:
【Python可视化系列】一文彻底教会你绘制美观的折线图(理论+源码)
【Python可视化系列】一文教会你绘制美观的柱状图(理论+源码)
对于一个连续性的变量,进行分布可视化最基本的图形是直方图(频度图)。每一个直方图进行可视化的时候都是分成两步的:(i) 把数据进行分组,首先把连续性的按照一定的范围进行分组,然后再统计这个范围的人数。(ii) 对上面分组的数据可视化,主要是通过类似条形图的方式来展示出来。
我将持续更新可视化的一些方法,关注我,不错过!本文将详细解读绘制直方图的要点!
二、实现过程
2.1 plt.hist()函数参数详解
函数功能:判定数据(或特征)的分布情况
调用方法:plt.hist(x, bins=10, range=None, normed=False, weights=None, cumulative=False, bottom=None, histtype='bar', align='mid', orientation='vertical', rwidth=None, log=False, color=None, label=None, stacked=False)
参数说明:
x:指定要绘制直方图的数据;
bins:指定直方图条形的个数;
range:指定直方图数据的上下界,默认包含绘图数据的最大值和最小值;
density:是否将直方图的频数转换成频率;
weights:该参数可为每一个数据点设置权重;
cumulative:是否需要计算累计频数或频率;
bottom:可以为直方图的每个条形添加基准线,默认为0;
histtype:指定直方图的类型,默认为bar,除此还有’barstacked’, ‘step’, ‘stepfilled’;
align:设置条形边界值的对其方式,默认为mid,除此还有’left’和’right’;
orientation:设置直方图的摆放方向,默认为垂直方向;
rwidth:设置直方图条形宽度的百分比;
log:是否需要对绘图数据进行log变换;
color:设置直方图的填充色;
label:设置直方图的标签,可通过legend展示其图例;
stacked:当有多个数据时,是否需要将直方图呈堆叠摆放,默认水平摆放;我们可以使用直方图来展现数据的分布,同过图形的长相,可以快速的判断数据是否近似服从正态分布。之所以我们很关心数据的分布,是因为在统计学中,很多假设条件都会包括正态分布,故使用直方图来定性的判定数据的分布情况,尤其显得重要。
2.2 基本直方图
# 读取数据集
heart = pd.read_csv(os.path.join(base_dir, 'data', 'UCI Heart Disease Dataset.csv'))
# 检查年龄是否有缺失
any(heart.age.isnull())
# 不妨删除含有缺失年龄的观察
heart.dropna(subset=['age'], inplace=True)
# 设置图形的显示风格
plt.style.use('ggplot')
# 字体设置
config = {
"font.family": 'Times New Roman, SimSun', # 衬线字体
"font.size": 12, # 相当于小四大小
"mathtext.fontset": 'stix', # matplotlib渲染数学字体时使用的字体,和Times New Roman差别不大
'axes.unicode_minus': False # 处理负号,即-号
}
plt.rcParams.update(config)
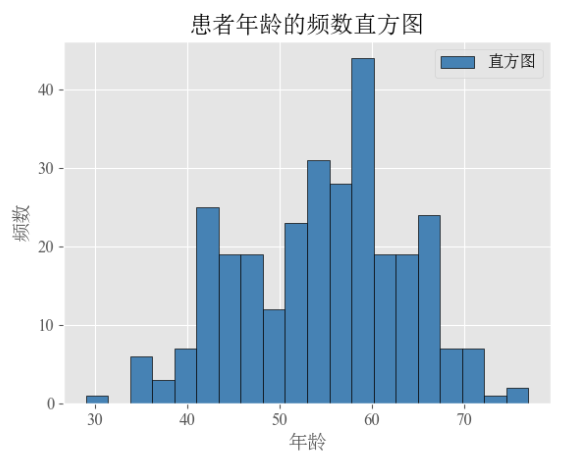
# 绘图:患者年龄的频数直方图
plt.hist(heart.age, # 绘图数据
bins = 20, # 指定直方图的条形数为20个
color = 'steelblue', # 指定填充色
edgecolor = 'k', # 指定直方图的边界色
label = '直方图' )# 为直方图呈现标签
plt.title('患者年龄的频数直方图')
plt.xlabel('年龄')
plt.ylabel('频数')
# 显示图例
plt.legend()
# 显示图形
plt.show()将数据中年龄切成20份,并计算每份患者的人数,得到如下直方图:
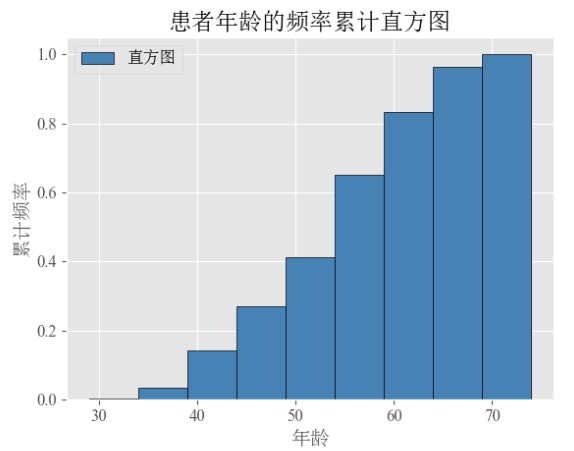
2.3 累计频率直方图
# 绘图:年龄的累计频率直方图
plt.hist(heart.age, # 绘图数据
bins = np.arange(heart.age.min(),heart.age.max(),5), # 指定直方图的组距
density = True, # 设置为频率直方图
cumulative = True, # 积累直方图
color = 'steelblue', # 指定填充色
edgecolor = 'k', # 指定直方图的边界色
label = '直方图' )# 为直方图呈现标签
# 设置坐标轴标签和标题
plt.title('患者年龄的频率累计直方图')
plt.xlabel('年龄')
plt.ylabel('累计频率')
# 显示图例
plt.legend(loc = 'best')
# 显示图形
plt.show()通过累计频率直方图就可以快速的发现到什么年龄段的人数占了多少比重
2.4 频率直方图和密度分布曲线图(密度图)
plt.hist(heart.age, # 绘图数据
bins = np.arange(heart.age.min(),heart.age.max(),5), # 指定直方图的组距
density = True, # 设置为频率直方图
color = 'steelblue', # 指定填充色
edgecolor = 'k') # 指定直方图的边界色
# 设置坐标轴标签和标题
plt.title('患者年龄频率直方图')
plt.xlabel('年龄')
plt.ylabel('频率')
# 生成正态曲线的数据
x1 = np.linspace(heart.age.min(), heart.age.max(), 1000)
normal = norm.pdf(x1, heart.age.mean(), heart.age.std())
# 绘制正态分布曲线
line1, = plt.plot(x1,normal,'r-', linewidth = 2)
# 生成核密度曲线的数据
kde = mlab.GaussianKDE(heart.age)
x2 = np.linspace(heart.age.min(), heart.age.max(), 1000)
# 绘制
line2, = plt.plot(x2,kde(x2),'g-', linewidth = 2)
# 显示图例
plt.legend([line1, line2],['正态分布曲线','核密度曲线'],loc='best')
# 显示图形
plt.show()为了测试数据是否近似服从正态分布,要在直方图的基础上再绘制两条线,一条表示理论的正态分布曲线,另一条为核密度曲线,目的就是比较两条曲线的吻合度,越吻合就说明数据越近似于正态分布。

补充:
密度图是与直方图密切相关的概念,它用一条连续的曲线表示变量的分布,可以理解为直方图的”平滑版本“。统计学经典理论假设样本数据来源于总体,而总体数据会服从某个分布(如正态分布,二项式分布等)。密度图采用”核密度统计量“来估计代表总体的随机变量的概率密度函数。直方图(频度图)观察数据的趋势,密度图观察数据的分布。
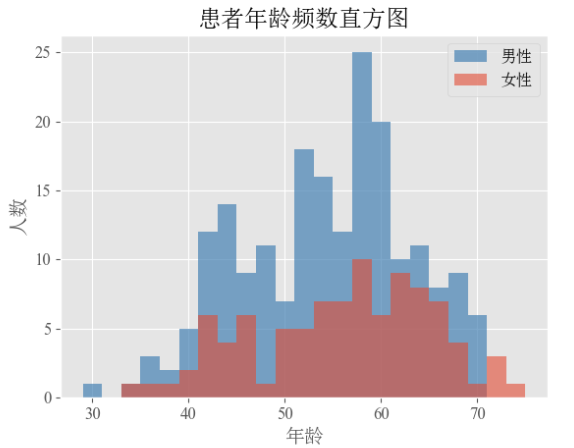
2.5 堆叠直方图
# 提取不同性别的年龄数据
age_female = heart.age[heart.sex == 0]
age_male = heart.age[heart.sex == 1]
# 设置直方图的组距
bins = np.arange(heart.age.min(), heart.age.max(), 2)
# 男性患者年龄直方图
plt.hist(age_male, bins = bins, label = '男性', color = 'steelblue', alpha = 0.7)
# 女性患者年龄直方图
plt.hist(age_female, bins = bins, label = '女性', alpha = 0.6)
# 设置坐标轴标签和标题
plt.title('患者年龄频数直方图')
plt.xlabel('年龄')
plt.ylabel('人数')
# 显示图例
plt.legend()
# 显示图形
plt.show()通过两个hist将不同性别的直方图绘制到一张图内,结果如下:
好了,本篇内容就总结分享到这里,需要源码的小伙伴可以关注底部公众号添加作者微信!
作者简介:
读研期间发表6篇SCI数据挖掘相关论文,现在某研究院从事数据算法相关科研工作,结合自身科研实践经历不定期分享关于Python、机器学习、深度学习、人工智能系列基础知识与应用案例。致力于只做原创,以最简单的方式理解和学习,关注我一起交流成长。