1. 【模板】前缀和

原题链接

---

题干：

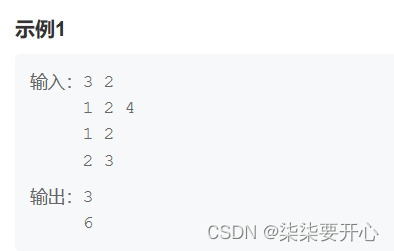
给定一个长度为 n 的数组
有 q 次查询，每次有两个参数 l 和 r

---

算法原理：

1. 暴力解法 （模拟）

这个时间复杂度是 O(n)

2. 前缀和（快速求出数组中某一个连续区间的和）

（1）预处理出来一个前缀和数组
dp[i] 表示：[1,i] 区间内所有元素的和

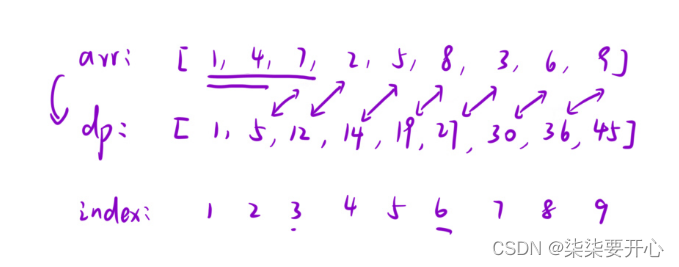
dp[i] = dp[i-1] + arr[i]

（2）使用前缀和数组

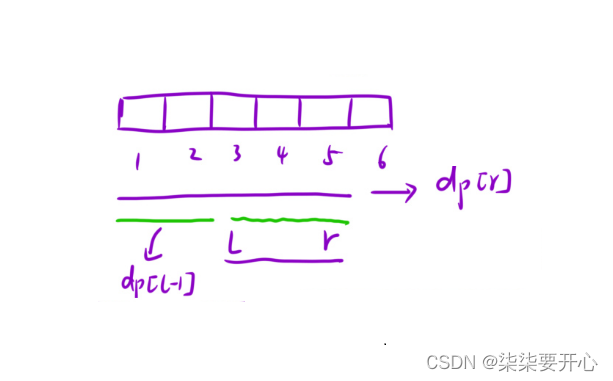
要求 [l,r] 中间的和
需要 dp[r] - dp[l-1]

细节问题：
为什么下标要从 1 开始技术
这是为了处理边界
因为如果是 0，-1就会数组异常

---

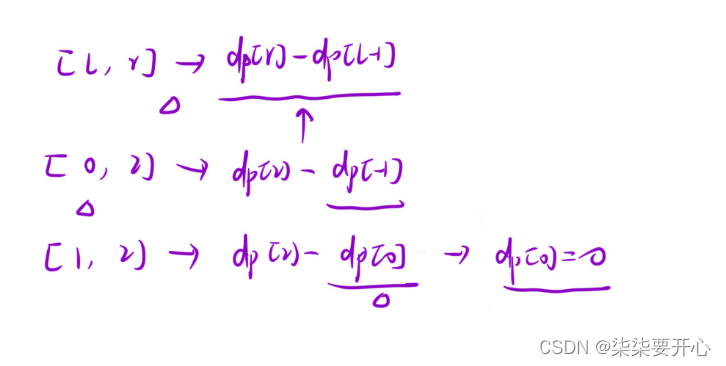
代码：

public class Main {
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        int n = in.nextInt();
        int q = in.nextInt();
        int[] arr = new int[n+1];
        long[] dp = new long[n+1];
        for(int i = 1; i <= n; i++) {
            arr[i] = in.nextInt();
        }
        for(int i = 1; i <= n; i++) {
            dp[i] = dp[i-1] + arr[i];
        }

        while(q > 0) {
            int l = in.nextInt();
            int r = in.nextInt();
            System.out.println(dp[r] - dp[l - 1]);
            q--;
        }
    }
}

---

2. 【模板】二维前缀和

原题链接

---

题干：

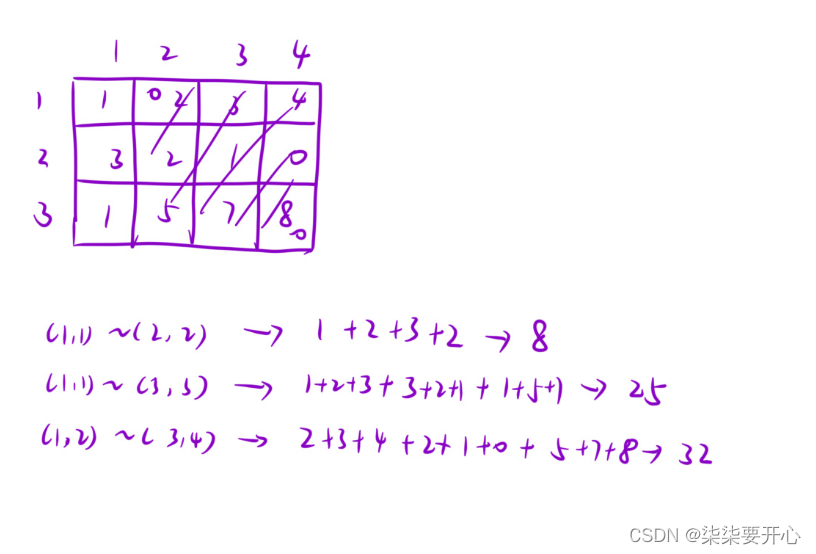
有一个 n*m 的矩阵
q 次查询 输入 x1 y1 x2 y2
输出以（x1，y1） 为左上角 和 （x2，y2）为右下角的子矩阵和

---

算法原理：

1. 暴力解法（模拟）

时间复杂度超过 O(n)

2. 前缀和

（1）预处理出来一个前缀和矩阵

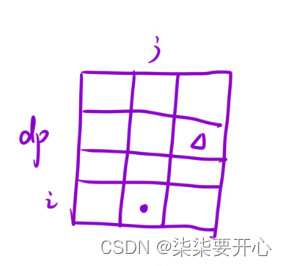
dp[i][j] 表示：从[1,1] 位置，这段区间里面所有元素的和

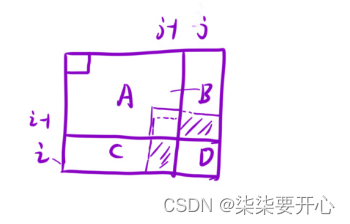
dp[i][j] = A + B + C + D = A + B + A + C + D - A
dp[i][j] = dp[i-1][j] +dp[i][j-1] +arr[i][j] - dp[i-1][j-1]

（2）使用前缀和矩阵

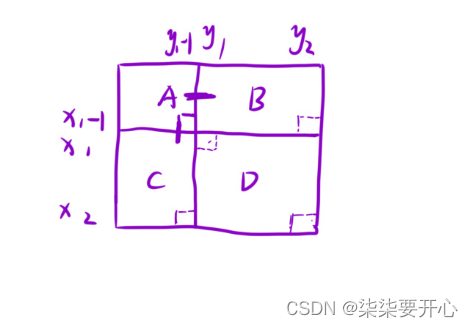
[x1,y1] ~ [x2,y2] 就是求 D 这一块的值
D = A + B + C + D - (A + B) - (A + C) + A
D = dp[x2][y2] - dp[x2][y1 - 1] - dp[x1- 1][y2] + dp[x1-
1][y2 - 1]

---

代码：

public class Main {
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        int n = in.nextInt();
        int m = in.nextInt();
        int[][] arr = new int[n+1][m+1];
        long[][] dp = new long[n+1][m+1];
        int q = in.nextInt();

        for(int i = 1; i <= n; i++) {
            for(int j = 1; j <= m; j++){
                arr[i][j] = in.nextInt();
            }
        }

        for(int i = 1; i <= n; i++) {
            for(int j = 1; j <= m; j++){
                dp[i][j] = dp[i-1][j] + dp[i][j-1] + arr[i][j] - dp[i-1][j-1];
            }
        }

        while(q > 0) {
            int x1 = in.nextInt();
            int y1 = in.nextInt();
            int x2 = in.nextInt();
            int y2 = in.nextInt();
            System.out.println(dp[x2][y2] - dp[x1 - 1][y2] - dp[x2][y1 - 1] + dp[x1 - 1][y1 - 1]);
            q--;
        }
    }
}

---

3. 地下城游戏

原题链接

---

题干：

---

算法原理：

1. 状态表示：

2. 状态转移方程

3. 初始化

4. 填表顺序

5. 返回值

---

代码：

class Solution {
    public int calculateMinimumHP(int[][] d) {
        int m = d.length;
        int n = d[0].length;
        int[][] dp = new int[m+1][n+1];

        for(int i = 0; i <= n; i++){
            dp[m][i] = Integer.MAX_VALUE;
        }
        for(int i = 0; i <= m; i++){
            dp[i][n] = Integer.MAX_VALUE;
        }
        dp[m][n-1] = dp[m-1][n] = 1;

        for(int i = m - 1; i >= 0; i--) {
            for(int j = n - 1; j >= 0; j--) {
                dp[i][j] = Math.min(dp[i][j+1], dp[i+1][j]) - d[i][j];
                dp[i][j] = Math.max(dp[i][j], 1);
            }
        }
        return dp[0][0];
    }
}