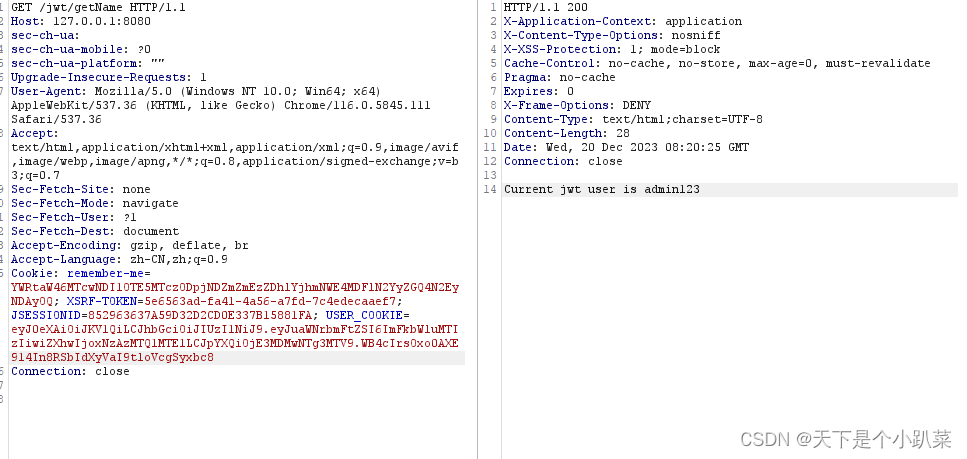
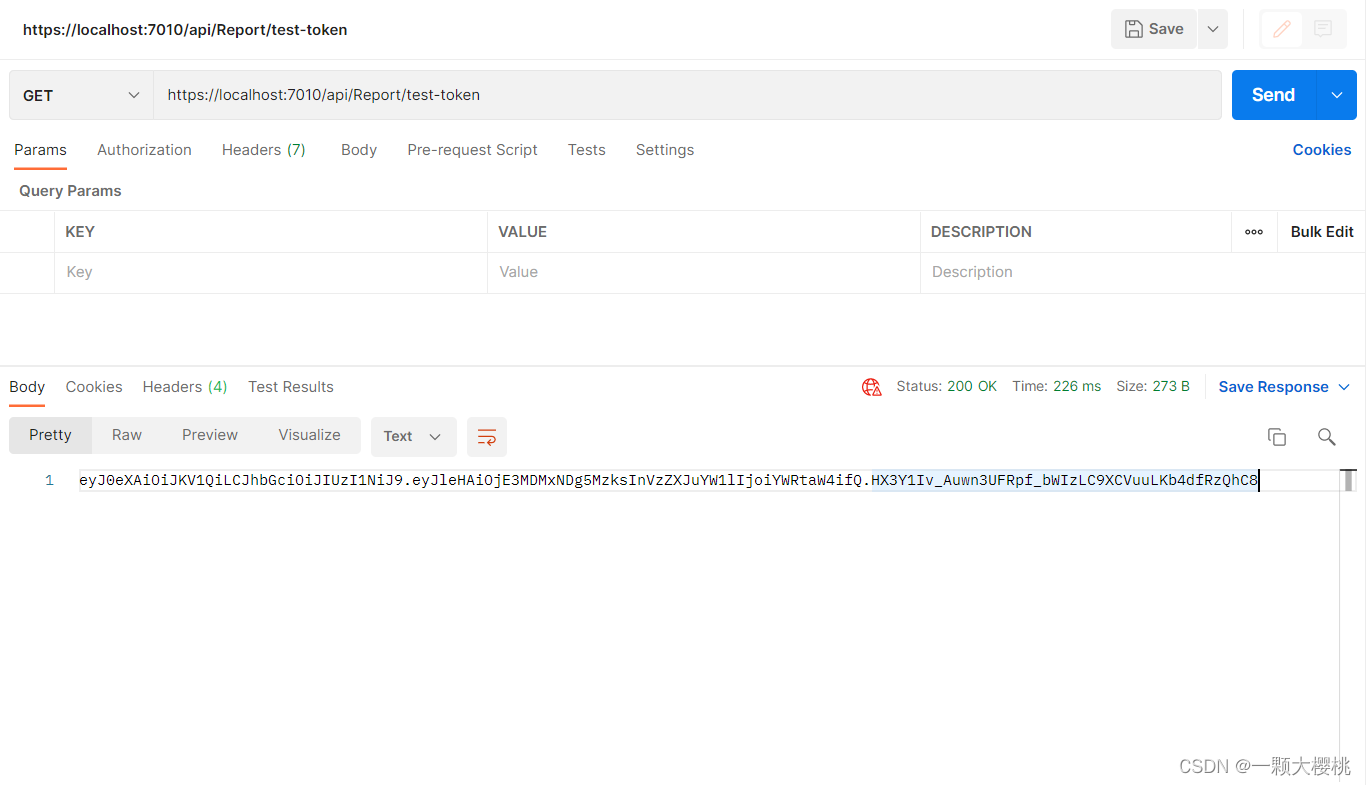
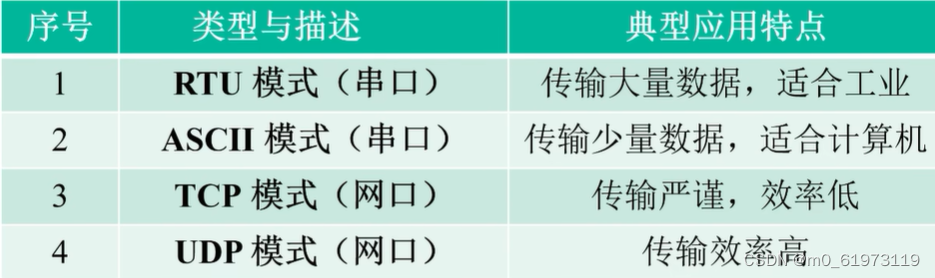
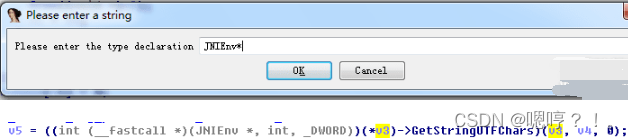
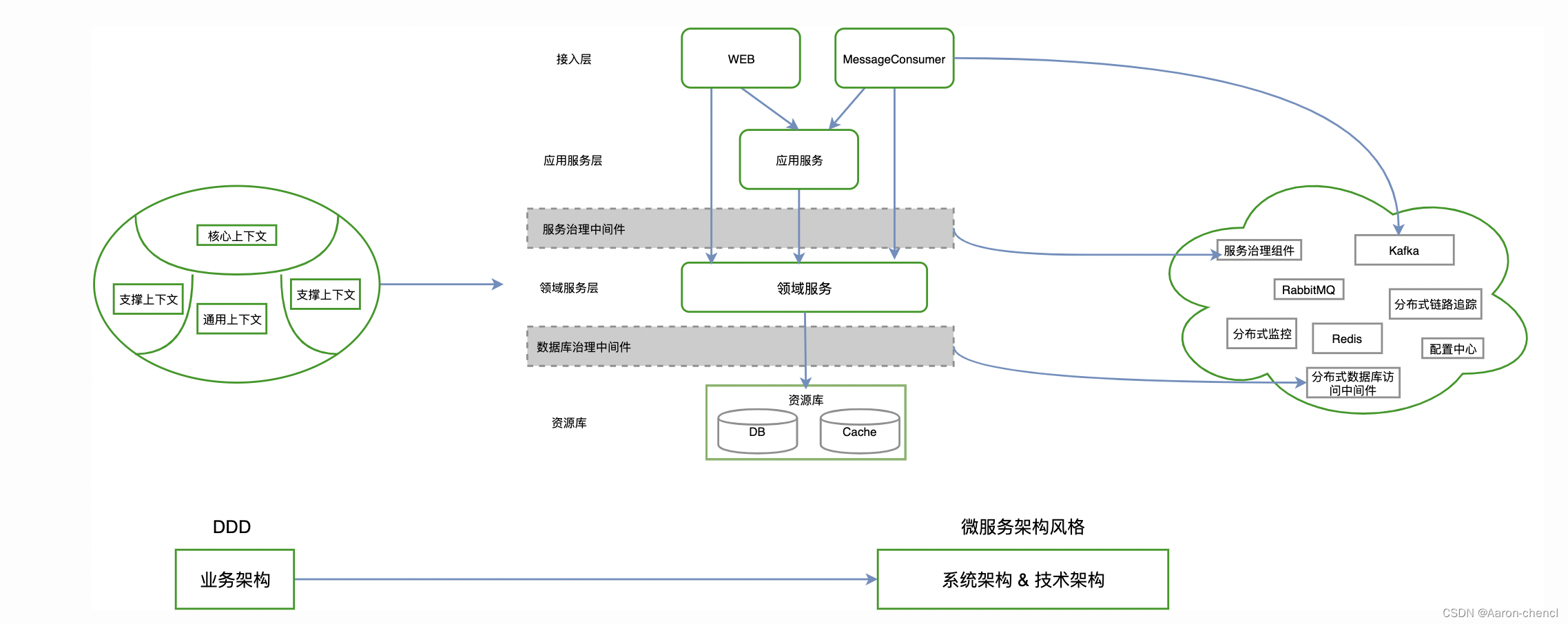
一、五种算法简介
1、鱼鹰优化算法OOA
2、鲸鱼优化算法WOA
3、灰狼优化算法GWO
4、蜣螂优化算法DBO
5、哈里斯鹰优化算法HHO
二、5种算法求解CEC2013
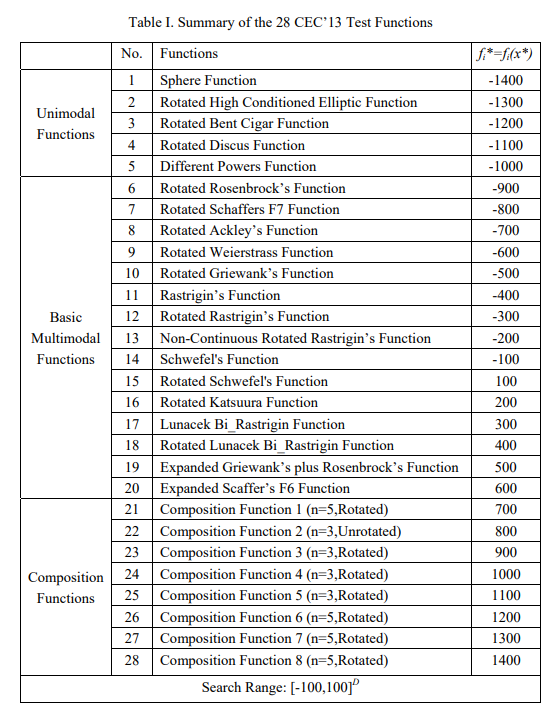
(1)CEC2013简介
参考文献:
[1] Liang J J , Qu B Y , Suganthan P N , et al. Problem Definitions and Evaluation Criteria for the CEC 2013 Special Session on Real-Parameter Optimization. 2013.
(2)部分python代码
from CEC2013.cec2013 import *
import numpy as np
from WOA import WOA
from GWO import GWO
from OOA import OOA
from HHO import HHO
from DBO import DBO
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['Microsoft YaHei']
#主程序
#主程序
function_name =14 #测试函数1-28
SearchAgents_no = 50#种群大小
Max_iter = 100#迭代次数
dim=10#维度 10/30/50/100
lb=-100*np.ones(dim)#下限
ub=100*np.ones(dim)#上限
cec_functions = cec2013(dim,function_name)
fobj=cec_functions.func#目标函数
BestX1,BestF1,curve1 = WOA(SearchAgents_no, Max_iter,lb,ub,dim,fobj)#问题求解
BestX2,BestF2,curve2 = GWO(SearchAgents_no, Max_iter,lb,ub,dim,fobj)#问题求解
BestX3,BestF3,curve3 = OOA(SearchAgents_no, Max_iter,lb,ub,dim,fobj)#问题求解
BestX4,BestF4,curve4 = HHO(SearchAgents_no, Max_iter,lb,ub,dim,fobj)#问题求解
BestX5,BestF5,curve5 = DBO(SearchAgents_no, Max_iter,lb,ub,dim,fobj)#问题求解
#画收敛曲线图
Labelstr=['WOA','GWO','OOA','HHO','DBO']
Colorstr=['r','g','b','k','c']
if BestF1>0:
plt.semilogy(curve1,color=Colorstr[0],linewidth=2,label=Labelstr[0])
plt.semilogy(curve2,color=Colorstr[1],linewidth=2,label=Labelstr[1])
plt.semilogy(curve3,color=Colorstr[2],linewidth=2,label=Labelstr[2])
plt.semilogy(curve4,color=Colorstr[3],linewidth=2,label=Labelstr[3])
plt.semilogy(curve5,color=Colorstr[4],linewidth=2,label=Labelstr[4])
else:
plt.plot(curve1,color=Colorstr[0],linewidth=2,label=Labelstr[0])
plt.plot(curve2,color=Colorstr[1],linewidth=2,label=Labelstr[1])
plt.plot(curve3,color=Colorstr[2],linewidth=2,label=Labelstr[2])
plt.plot(curve4,color=Colorstr[3],linewidth=2,label=Labelstr[3])
plt.plot(curve5,color=Colorstr[4],linewidth=2,label=Labelstr[4])
plt.xlabel("Iteration")
plt.ylabel("Fitness")
plt.xlim(0,Max_iter)
plt.title("cec2013-F"+str(function_name))
plt.legend()
plt.savefig(str(function_name)+'.png')
plt.show()
#

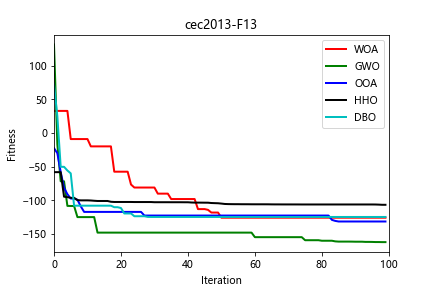
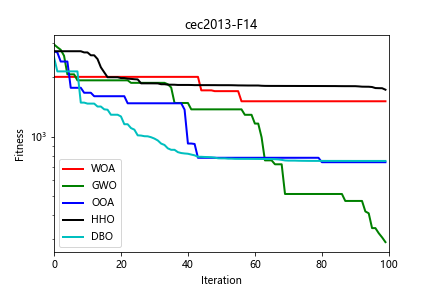
(3)部分结果





三、完整python代码