本文涉及几何问题,求角平分线,垂直平分线以及中线,不止可以应用于点和三角形,其他需求可选择性提取。
求角平分线:http://t.csdnimg.cn/QYZOK
求垂直平分线:http://t.csdnimg.cn/A4wWD
三角形的重心,外心,垂心,内心和旁心称之为三角形的五心。三角形的中心一般为三角形的重心,重心为三角形三边中线交点。
外心,即三角形外接圆圆心,为三角形三边垂直平分线的交点。
内心,即三角形内切圆圆心,为三角形三角的角平分线的交点。其他两心这里不展开介绍。
下面是待处理图片,求这三点的中心,三角形外接圆以及三角形内切圆。

图片中是三个圆孔,先求圆心,再连接得到三角形
*1.边缘检测
edges_sub_pix (Image, Edges, 'canny', 1, 20, 40)
segment_contours_xld (Edges, ContoursSplit, 'lines_circles', 5, 4, 2)
select_shape_xld (ContoursSplit, SlectedXLD, 'circularity', 'and', 0.5, 1.0)
*拟合圆,得到各圆圆心坐标
fit_circle_contour_xld (SlectedXLD, 'algebraic', -1, 0, 0, 3, 2, Row, Column, Radius, StartPhi, EndPhi, PointOrder)
gen_circle (CircleA, Row[0], Column[0], Radius[0])
gen_circle (CircleB, Row[1], Column[1], Radius[1])
gen_circle (CircleC, Row[2], Column[2], Radius[2])
dev_set_draw ('margin')
dev_set_color ('pink')
dev_display (CircleA)
dev_display (CircleB)
dev_display (CircleC)
*绘制三角形三边,以圆心坐标定顶点
gen_region_line (RegionLines01, Row[0], Column[0], Row[1], Column[1])
gen_region_line (RegionLines02,Row[0], Column[0], Row[2], Column[2])
gen_region_line (RegionLines12, Row[1], Column[1], Row[2], Column[2])
union2 (RegionLines01, RegionLines02, RegionUnion1)
union2 (RegionLines12, RegionUnion1, RegionUnion)
gen_contour_region_xld (RegionUnion, TriangleContour, 'border')
dev_set_color ('blue')
dev_display (TriangleContour)得到三角形如下:
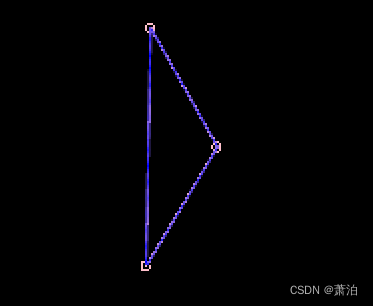
因为这里需要分别对三个点和三条边做处理,可以选择创建新函数,后面直接调参使用,减少冗余步骤。
选中编辑好的函数,右键点击“创建新函数”,

确定需要的输入参数和输出参数,函数中内部可以生成或‘消化’的参数可以移除。

上面部分是都需要做处理的,下面的根据需求选择。
1.求三角形重心
我也理解为求取三点中心,这个没有资料可以确定。可以连接三点为三角形,求其重心。
gen_contour_region_xld (RegionLines01, Contours01, 'border')
*获取直线中点
area_center_points_xld (Contours01, Area, Row01, Column01)
gen_region_line (MidLines01, Row01, Column01, Row2, Column2)
gen_contour_region_xld (MidLines01, MidContour01, 'border')
dev_set_color ('spring green')
dev_display (MidContour01)
return ()选中以上代码,创建新函数
drawline_midian ( RegionLines01 : MidContour01 : Row2, Column2 : )
参数依次为输入边,输出中线,输入边的对边顶点坐标。
对三角形三边都调用上面的函数求取中线,再求取交点:
*求三角形中心,即重心,三边中线交点
drawline_midian (RegionLines01, MidContour01, Row2, Column2)
drawline_midian (RegionLines02, MidContour02, Row[1], Column[1])
drawline_midian (RegionLines12, MidContour12, Row[0], Column[0])
*求交点
intersection_contours_xld (MidContour01, MidContour02, 'mutual', RowCentroid, ColumnCentroid, IsOverlapping3)
dev_set_color ('white')
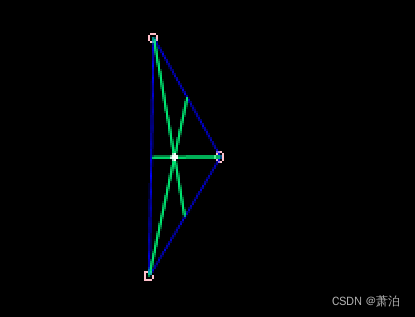
disp_cross (WindowHandle, RowCentroid, ColumnCentroid, 20, 0)
运行得到如下效果,图中白色交点为三角形中心和重心,我也理解为这三点的中心(存疑)。
2.求三角形外接圆
对以下代码部分创建新函数:
gen_contour_region_xld (RegionLines1, Contours1, 'border')
*获取直线角度
elliptic_axis_points_xld (Contours1, Ra1, Rb1, Phi1)
*获取直线中点
area_center_points_xld (Contours1, Area, Row1, Column1)
*垂线长度,可以调整数值,延长线的长度,利用角度比例关系
LineLength:=400
*起点
RowStart := Row1-cos(Phi1)*LineLength
ColStart := Column1-sin(Phi1)*LineLength
*终点
RowEnd := Row1+cos(Phi1)*LineLength
ColEnd := Column1+sin(Phi1)*LineLength
gen_region_line (MidnormalLine1, RowStart, ColStart, RowEnd, ColEnd)
gen_contour_region_xld (MidnormalLine1, MidnormalContour, 'border')
dev_set_color ('magenta')
dev_display (MidnormalContour)
return ()drawline_midnormal ( RegionLines1 : MidnormalContour : : LineLength )
参数依次为:输入边,输出垂直平分线,垂直平分线的长度
求交点:

这里的交点是求取两条线的轮廓的交点,由于轮廓没有特别精细,识别出来的交点是一小块区域包含了非常相近的多组行列坐标[]。因为差别不大,本文需求不需要特别精细,这里选取了第一组行列坐标Row[0],Column[0]。
*求外接圆,求三边垂直平分线
drawline_midnormal (RegionLines01, MidnormalContour1, LineLength)
drawline_midnormal (RegionLines02, MidnormalContour2, LineLength)
drawline_midnormal (RegionLines12, MidnormalContour3, LineLength)
*求交点
intersection_contours_xld (MidnormalContour1, MidnormalContour2, 'mutual', RowCenter, ColumnCenter, IsOverlapping2)
dev_set_color ('red')
disp_cross (WindowHandle, RowCenter[0], ColumnCenter[0], 20, 0)
*计算圆心到三角形顶点距离
distance_pp (Row[0], Column[0], RowCenter[0], ColumnCenter[0], DistanceR)
*绘制外接圆
gen_circle_contour_xld (Circumcircle, RowCenter[0], ColumnCenter[0], DistanceR, 0, 6.28318, 'positive', 1)
disp_cross (WindowHandle, RowCenter, ColumnCenter, 20, 0)
dev_display (Circumcircle)外接圆到各个顶点的半径一样,这里选取任意顶点到交点的距离作为半径画圆,效果如下:

3.求三角形内切圆
求取角平分线在代码里实现这个过程比较复杂,可以参考文章最上面的链接结合图片理解:
这里简单介绍一下:
(1)分别对三个顶点重新画同半径大小的圆(可以小一点),每个顶点的圆都会与角两边有交点;
(2)得到六个交点;
(3)分别对六个交点重新画同半径大小的圆(可以大一点),每个角的方向画出来的两个圆会得到两个交点,连接两个交点即为角平分线。
(4)延长角平分线。(可以求取线性方程,或者自定义长度,2和3的代码中延长线方法不一样)

对以下代码部分创建新函数,
*以圆心重新绘制圆,半径自定义,大圆方便观察
gen_circle_contour_xld (ContCircleA, Row, Column, 50, 0, 6.28318, 'positive', 1)
dev_set_color ('green')
dev_display (ContCircleA)
*获取圆与三角形轮廓的交点
intersection_contours_xld (TriangleContour, ContCircleA, 'all', Rowa, Columna, IsOverlapping0)
*以交点为圆心画两个同半径圆,两圆交点与三角形顶点连线角平分线
gen_circle_contour_xld (ContCircleA1, Rowa[0], Columna[0], 80, 0, 6.28318, 'positive', 1)
gen_circle_contour_xld (ContCircleA2, Rowa[1], Columna[1], 80, 0, 6.28318, 'positive', 1)
intersection_contours_xld (ContCircleA1, ContCircleA2, 'all', Row1, Column1, IsOverlapping)
* gen_region_line (RegionLines, Row1[0], Column1[0], Row1[1], Column1[1])
* gen_contour_region_xld (RegionLines, AngleBisectors, 'border')
*延长角平分线,求线性方程
r:= Row1[0] - Row1[1]
n:= Column1[0] - Column1[1]
k1:= r/n
b1:=Row1[1] - k1*Column1[1]
row11:=k1*1100+b1
row12:=k1*1500+b1
dev_set_color ('yellow')
disp_line (WindowHandle, row11, 1100, row12, 1500)
gen_region_line (RegionLines, row11, 1100, row12, 1500)
gen_contour_region_xld (RegionLines, AngleBisectors, 'border')
return ()求取交点,并求交点到三角形三边的最短距离作半径画圆:
*求内切圆,找角平分线并延长
drawline_angle_bisector (TriangleContour, AngleBisectorsA, Row[0], Column[0], WindowHandle)
drawline_angle_bisector (TriangleContour, AngleBisectorsB, Row[1], Column[1], WindowHandle)
drawline_angle_bisector (TriangleContour, AngleBisectorsC, Row2, Column2, WindowHandle)
*求圆心,intersection_lines用直线坐标求,intersection_contours_xld用轮廓求
intersection_contours_xld (AngleBisectorsA, AngleBisectorsB, 'mutual', CenterRow, CenterColumn, IsOverlapping1)
*求圆心到三角形边的最短距离
distance_pc (TriangleContour, CenterRow, CenterColumn, DistanceMin, DistanceMax)
gen_circle_contour_xld (CenterCircle, CenterRow, CenterColumn, DistanceMin, 0, 6.28318, 'positive', 1)
dev_set_color ('violet red')
disp_cross (WindowHandle, CenterRow, CenterColumn, 20, 0)
dev_display (CenterCircle)效果如下:

再整理一下延长线的方法吧.
4.延长直线
已得到直线上的两个以上的点,Row[ ],Column[ ]为直线上的坐标数组。
(1)求线性方程
任意选取两个点的坐标求线性方程y=ax+b。
*延长角平分线
r:= Row[0] - Row[1]
n:= Column[0] - Column[1]
k1:= r/n
b1:=Row[1] - k1*Column[1]
*定义起始坐标和结束坐标
colstart:=1100
colend:=1500
rowstart:=k1*colstart+b1
rowend:=k1*colend+b1
dev_set_color ('yellow')
disp_line (WindowHandle, rowstart, colstart, rowend, colend)
gen_region_line (RegionLines, rowstart, colstart, rowend, colend)
gen_contour_region_xld (RegionLines, AngleBisectors, 'border')
(2)利用直线角度比例
gen_region_line (RegionLines1, Row[0], Column[0], Row[1], Column[1])
gen_contour_region_xld (RegionLines1, Contours1, 'border')
*获取直线角度
elliptic_axis_points_xld (Contours1, Ra1, Rb1, Phi1)
*获取直线中点
area_center_points_xld (Contours1, Area, Row1, Column1)
*垂线长度
LineLength:=400
*起点
RowStart := Row1-cos(Phi1)*LineLength
ColStart := Column1-sin(Phi1)*LineLength
*终点
RowEnd := Row1+cos(Phi1)*LineLength
ColEnd := Column1+sin(Phi1)*LineLength
gen_region_line (MidnormalLine1, RowStart, ColStart, RowEnd, ColEnd)
gen_contour_region_xld (MidnormalLine1, MidnormalContour, 'border')OKOK,下班,又困又饿。