CGAL中流线的二维放置

news2024/9/25 17:21:21

本章介绍CGAL 2D流线放置包。定义一节给出了基本定义和概念。基本概念一节对整合过程进行了描述。最远点播种策略一节简要介绍了该算法。“实现”一节介绍了包的实现，“示例”一节详细介绍了两个示例放置。

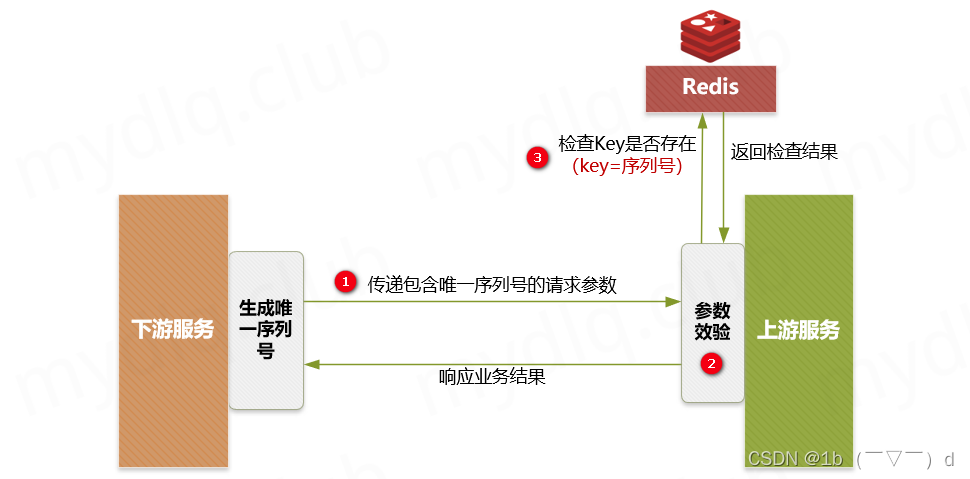
该算法的核心思想是对域中最大空腔中心的流线进行积分（左）。所有采样点的Delaunay三角测量用于对域（中间）内的流线和空间进行建模。最终结果如图所示（右）。

1、定义

在物理学中，场是对空间中的每个点分配一个量。例如，引力场为空间中的每个点指定一个引力势。

矢量场和方向场通常用于建模物理现象，其中方向和大小，即矢量被分配给域内的每个点（例如磁场中每个点处的力的大小和方向）。

流线是可视化流场的重要工具。流线*是一条处处与场相切的曲线。在实践中，流线通常表示为从种子点开始通过双向数值积分迭代拉长的多段线（一系列点），直到它接近另一条流线（根据称为分离距离的指定距离）、到达域边界、到达临界点或生成闭合路径。

流线的有效放置包括根据流线之间的分离距离确定的指定密度，用一组切向流线饱和域。

2、基本概念

流线可以被认为是一个假想的无质量粒子落入由场描述的稳定流体流中所追踪的路径。这条路径的构造包括求解连续时间间隔的常微分方程。通过这种方式，我们获得了一系列点pk，0<k<n，这些点允许可视化流线。微分方程定义如下：

dp/dt=v(p(t)), p(0)=p0

其中p（t）是粒子在时间t的位置，v是在域中的每个点分配矢量值的函数（可能通过插值），p0是初始位置。给定间隔Δt之后的位置由下式给出：

p(t+Δt)=p(t)+∫t+Δttv(p(t))dt

已经提出了几种数值方法来求解这个方程。在这个程序包中，实现了欧拉和二阶龙格-库塔算法。

2.1、欧拉积分器

这个算法用这个公式近似计算点：pk+1=pk+hv(pk)。

其中，h指定积分步骤*。可以通过指定正（或负）积分步骤h向前（或向后）进行积分。然后，通过从种子点向前和向后连续积分来构建流线。

2.2、二阶龙格-库塔积分器

龙格-库塔二阶积分器（空圆表示中间点，灰盘表示欧拉积分点）。

该方法在pk和pk+1之间引入了一个中间点p′k，以提高计算精度，其中：

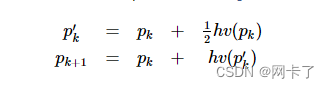
3、最远点播种策略

该软件包中实现的算法包括通过数值积分一次放置一条流线，从距离所有先前放置的流线最远的地方开始。

我们的算法的输入由

（i）流场，（ii）由理想间距的倒数全局指定的密度，或由密度场局部指定的密度和（iii）触发新流线的播种所需的期望间距的饱和比给出。

输入流场由在域内采样的矢量或方向的离散集给出，该离散集与插值方案相关（例如，规则网格上的双线性插值，或不规则点集上的自然邻居插值，以允许在域内的每个点坐标处进行评估）。

输出是流线放置，表示为流线列表。我们算法的核心思想是通过在距离所有先前放置的流线最远的点播种的数值积分，一次放置一条流线。

流线由多段线近似，多段线的点插入二维Delaunay三角测量。Delaunay三角形的空外接圆为我们提供了域中空腔的良好近似。

在每次流线积分后，所有外接圆直径大于（在饱和比内）所需间距的入射三角形都被推送到按三角形外接圆半径排序的优先队列中。为了开始每个新的流线积分，将从队列中弹出外接圆直径最大的三角形（因此也是最大的空腔）。我们首先测试它是否仍然是三角测量的有效三角形，因为它可能已经被之前添加到三角测量中的流线破坏。如果不是，我们从队列中弹出另一个三角形。如果是，我们使用其外接圆的中心作为种子点来集成新的流线。

当优先级队列为空时，我们的算法终止。最大空腔的大小是单调递减的，我们的算法保证了域饱和。