一、概述

已经证明 Point -to-Plane 算法已经比Point-to-Point 的误差都要快更准确一些，在 ICP 算法的每次选代中，产生最小点到平面误差的相对位姿变化通常使用标准的非线性最小二乘法来解决。例如 Levenberg-Marquardt方法。当使用点到平面误差度量时，最小化的对象是每个源点与其对应目标点的切平面之间的平方距离之和。

二、原理介绍

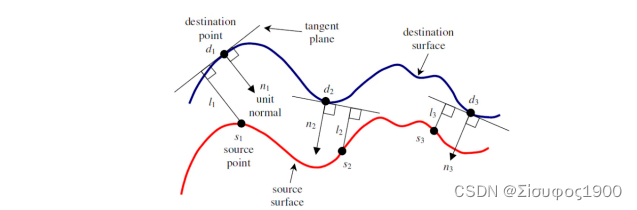
那么我们可以计算间距最小函数，即loss 函数

                                                     

参数注释：

         R：表示的是旋转矩阵

         T：表示的是 平移矩阵

         Pi： 表示的是soruce 点云

         Qi：表示的是target 点云

         Ni：表示的是target点云该点对于的法向量

 推导：

点云配准: 刚性ICP中 Point-to-Point 和 Point-to-Plane 公式推导 ==> 帮助你代码实现 - 知乎

准备1 

 

                     

 

 

点云刚性配准：point2point 和 point2plane 代码 - 知乎

void ICP::point2plane(float weight, Eigen::MatrixXf& A, Eigen::VectorXf& b)
{

	A.resize(m_srcOfPair.size(), 6);
	b.resize(m_srcOfPair.size());

	for (int j = 0; j < m_srcOfPair.size(); j++)
	{
		Eigen::Vector3f sourceCoordinates;
		sourceCoordinates = m_srcOfPair[j];

		Eigen::Vector3f targetCoordinates;
		targetCoordinates = m_targetOfPair[j];

		Eigen::Vector3f targetNormal;
		targetNormal = m_targetNormalsOfPair[j];

		//两个向量的叉乘结果是一个向量（三个数）
		Eigen::Vector3f sourceMultiplyNormal;
		sourceMultiplyNormal = sourceCoordinates.cross(targetNormal);

		A(j, 0) = sourceMultiplyNormal[0];
		A(j, 1) = sourceMultiplyNormal[1];
		A(j, 2) = sourceMultiplyNormal[2];
		A(j, 3) = targetNormal[0];
		A(j, 4) = targetNormal[1];
		A(j, 5) = targetNormal[2];

		b[j] = -(((sourceCoordinates - targetCoordinates).transpose()).dot(targetNormal));
	}

	A *= weight;
	b *= weight;

}