机器学习 | 贝叶斯方法

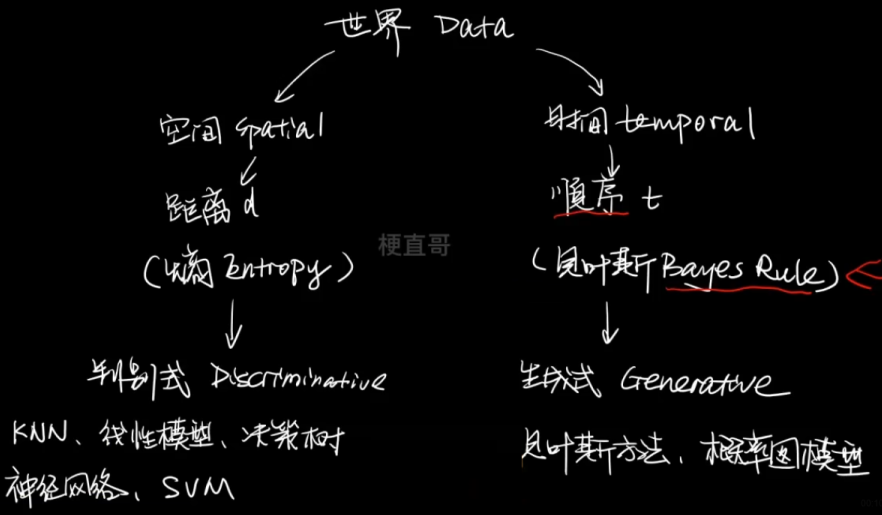
不同于KNN最近邻算法的空间思维，线性算法的线性思维，决策树算法的树状思维，神经网络的网状思维，SVM的升维思维。

贝叶斯方法强调的是先后的因果思维。

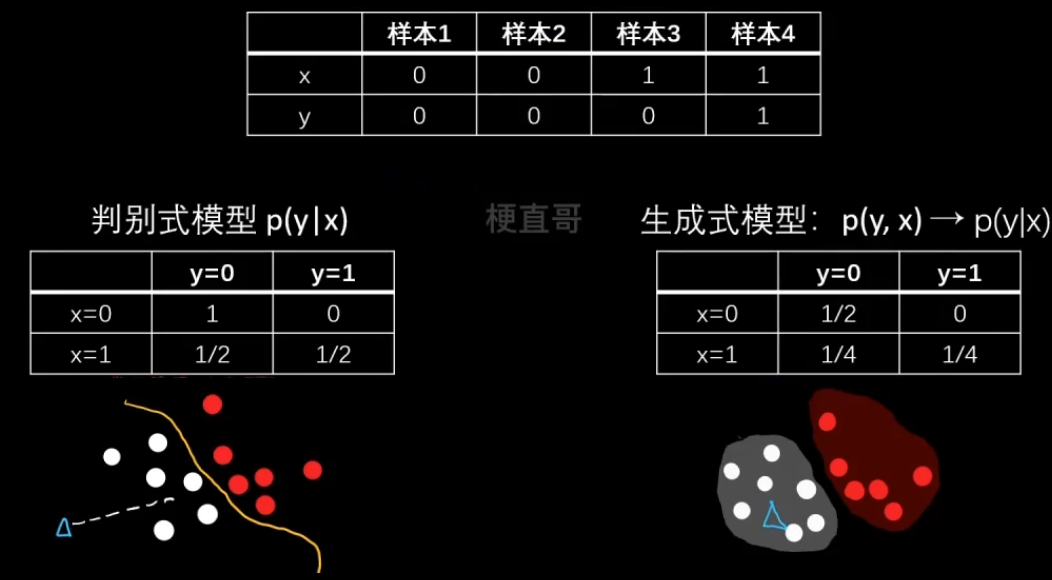
监督式模型分为判别式模型和生成式模型。

判别模型和生成模型的区别：

判别式模型：输入一个特征X可以直接得到一个y。

生成式模型：上来先学习一个联合概率分布 p(x,y)，

再用他根据贝叶斯法则求条件概率密度分布。

—— 没有决策边界的存在

判别式数据对于数据分布特别复杂的情况，比如文本图像视频；

而生成式模型对于数据有部分特征缺失的情况下效果更好，

而且更容易添加数据的先验知识 p(x)

1、核心思想和原理

贝叶斯公式

建立了四个概率分布之间的关系，已知变量 X 和未知变量（模型参数）w 之间的计算关系

假定 X 表示数据，W 表示模型的参数

Likelihood翻译成可能性或者是似然函数，最大似然估计指的就是这个

以下图中 s 表示状态， o 表示观测。

参数估计

1、最大似然估计 MLE

2、最大后验估计 MAP

3、贝叶斯估计

2、朴素贝叶斯分类

我们知道分类问题是给定特征 X，输出分类标记 y

那么朴素贝叶斯方法是如何由指定特征得到分类类别的呢？

2.1、举个栗子

能不能直接根据这些经验（上面的数据），来判断一个境外人员有没有得新冠呢？

—— 转换为数学语言即

比较难求的显然就是 Likelihood，所以朴素贝叶斯假设特征之间相互独立。

根据中心极限定理，频率就等于概率，虽然这里数据没有那么多，也一样可以这么算

2.2、朴素贝叶斯分类及其代码实现

逻辑简单，易于实现
效率高，时空开销小
条件独立假设不成立则分类效果一般
适用于特征相关性较小时

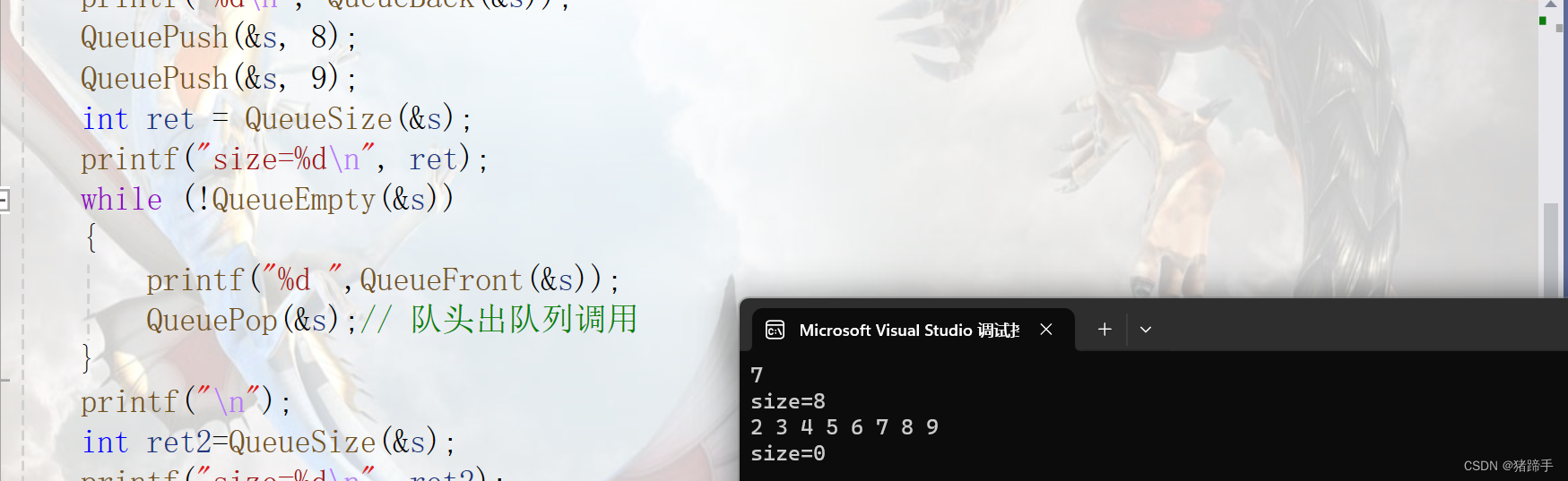
代码实现：

import numpy as np

X = [[1,0,0,1],
     [0,1,0,0],
     [1,1,0,0],
     [0,1,2,0],
     [1,0,0,0],
     [1,0,0,0],
     [1,1,2,1],
     [0,1,1,0],
     [1,1,1,0],
     [0,0,2,0],
     [1,1,0,1],
     [1,1,0,1]]

y = [0,0,1,1,0,0,1,1,1,1,0,0]

t=[[0,0,0,1]]

from sklearn.naive_bayes import BernoulliNB

bnb = BernoulliNB()
bnb.fit(X,y)
bnb.predict_proba(t)

array([[0.875, 0.125]])

2,3、朴素贝叶斯家族

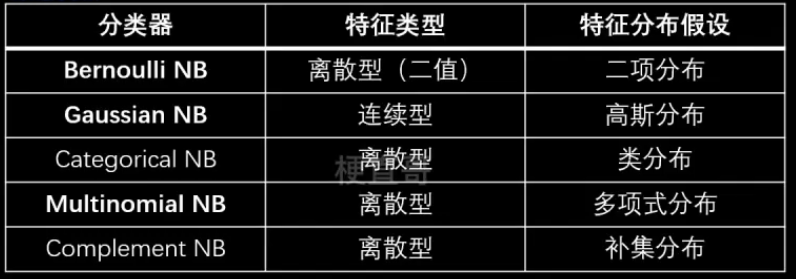
2.3.1、伯努利朴素贝叶斯与多项式朴素贝叶斯

伯努利分布（两点分布、0-1分布）

属于离散型概率分布

伯努利分布公式：

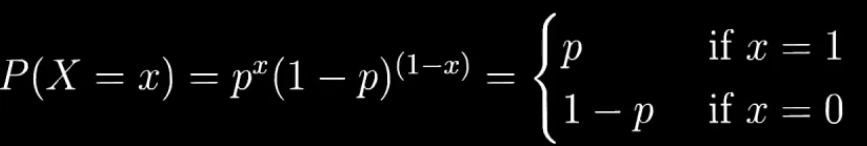
伯努利实验 —— 例如抛硬币。

二项式分布和多项式分布

二项式分布：伯努利实验重复n次。

n = 1的二项式分布就是伯努利分布。

多项式分布：抛硬币改为掷骰子。

伯努利朴素贝叶斯：每个特征都服从伯努利分布的一种贝叶斯分类器

适用于二分类离散变量。

特征的条件概率服从伯努利分布：

xi 表示第 i 哥特征维度，y 表示观测道德类别。

特征可选值大于两个时可用多项式分布。

2.3.2、高斯朴素贝叶斯

2.4、分类器效果对比

from sklearn.datasets import load_iris

iris = load_iris()
X = iris.data
y = iris.target
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=0)

from sklearn.naive_bayes import BernoulliNB
nb = BernoulliNB()
nb.fit(X_train, y_train)
nb.score(X_test, y_test)

0.23684210526315788

print(iris.DESCR)

.. _iris_dataset:

Iris plants dataset
--------------------

**Data Set Characteristics:**

    :Number of Instances: 150 (50 in each of three classes)
    :Number of Attributes: 4 numeric, predictive attributes and the class
    :Attribute Information:
        - sepal length in cm
        - sepal width in cm
        - petal length in cm
        - petal width in cm
        - class:
                - Iris-Setosa
                - Iris-Versicolour
                - Iris-Virginica
                
    :Summary Statistics:

    ============== ==== ==== ======= ===== ====================
                    Min  Max   Mean    SD   Class Correlation
    ============== ==== ==== ======= ===== ====================
    sepal length:   4.3  7.9   5.84   0.83    0.7826
    sepal width:    2.0  4.4   3.05   0.43   -0.4194
    petal length:   1.0  6.9   3.76   1.76    0.9490  (high!)
    petal width:    0.1  2.5   1.20   0.76    0.9565  (high!)
    ============== ==== ==== ======= ===== ====================

    :Missing Attribute Values: None
    :Class Distribution: 33.3% for each of 3 classes.
    :Creator: R.A. Fisher
    :Donor: Michael Marshall (MARSHALL%PLU@io.arc.nasa.gov)
    :Date: July, 1988

The famous Iris database, first used by Sir R.A. Fisher. The dataset is taken
from Fisher's paper. Note that it's the same as in R, but not as in the UCI
Machine Learning Repository, which has two wrong data points.

This is perhaps the best known database to be found in the
pattern recognition literature.  Fisher's paper is a classic in the field and
is referenced frequently to this day.  (See Duda & Hart, for example.)  The
data set contains 3 classes of 50 instances each, where each class refers to a
type of iris plant.  One class is linearly separable from the other 2; the
latter are NOT linearly separable from each other.

.. topic:: References

   - Fisher, R.A. "The use of multiple measurements in taxonomic problems"
     Annual Eugenics, 7, Part II, 179-188 (1936); also in "Contributions to
     Mathematical Statistics" (John Wiley, NY, 1950).
   - Duda, R.O., & Hart, P.E. (1973) Pattern Classification and Scene Analysis.
     (Q327.D83) John Wiley & Sons.  ISBN 0-471-22361-1.  See page 218.
   - Dasarathy, B.V. (1980) "Nosing Around the Neighborhood: A New System
     Structure and Classification Rule for Recognition in Partially Exposed
     Environments".  IEEE Transactions on Pattern Analysis and Machine
     Intelligence, Vol. PAMI-2, No. 1, 67-71.
   - Gates, G.W. (1972) "The Reduced Nearest Neighbor Rule".  IEEE Transactions
     on Information Theory, May 1972, 431-433.
   - See also: 1988 MLC Proceedings, 54-64.  Cheeseman et al"s AUTOCLASS II
     conceptual clustering system finds 3 classes in the data.
   - Many, many more ...

from sklearn.naive_bayes import GaussianNB
nb = GaussianNB()
nb.fit(X_train, y_train)
nb.score(X_test, y_test)

1.0

from sklearn.naive_bayes import CategoricalNB
nb = CategoricalNB()
nb.fit(X_train, y_train)
nb.score(X_test, y_test)

0.8947368421052632

from sklearn.naive_bayes import MultinomialNB
nb = MultinomialNB()
nb.fit(X_train, y_train)
nb.score(X_test, y_test)

0.5789473684210527

from sklearn.naive_bayes import ComplementNB
nb = ComplementNB()
nb.fit(X_train, y_train)
nb.score(X_test, y_test)

0.5789473684210527

2.5、多项式朴素贝叶斯代码实现

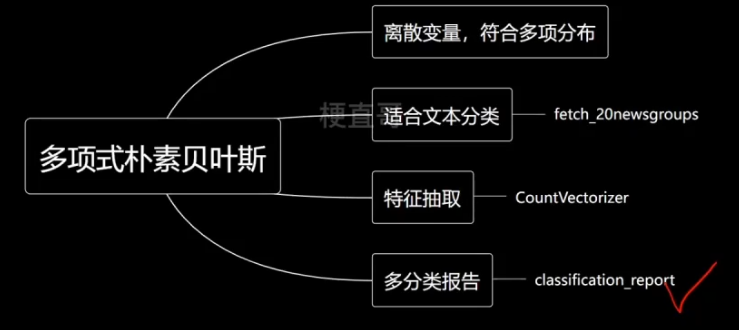
纯文本数据不能直接传入模型，需要进行特征抽取。

Chapter-10/10-6 多项式朴素贝叶斯代码实现.ipynb · 梗直哥/Machine-Learning - Gitee.com

3、优缺点和使用条件

朴素贝叶斯优点

过程简单速度快。

对多分类问题言样有效。

分布独立假设下效果好。

贝叶斯思想光芒万丈，先验打开“扇大门。（拓展变分）

朴素贝叶斯缺点

条件独立假设在现实中往往很难保证。

只适用于简单比大小问题。

如果个别类别概率为0，则预测失败。（平滑技术解决）。

条件概率和先验分布计算复杂度较高，高维计算困难。

适用条件

文本分类/垃圾文本过滤/情感判别。

多分类实时预测。

推荐系统、与协同过滤一起。

复杂问题建模。

参考

Machine-Learning: 《机器学习必修课：经典算法与Python实战》配套代码 - Gitee.com