在确定了训练集 D、假设空间 ℱ 以及学习准则后,如何找到最优的模型𝑓(x,θ∗) 就成了一个最优化(Optimization)问题。机器学习的训练过程其实就是最优化问题的求解过程。
参数与超参数 在机器学习中,优化又可以分为参数优化和超参数优化。模型𝑓(x;θ)中的θ称为模型的参数,可以通过优化算法进行学习。除了可学习的参数θ之外,还有一类参数是用来定义模型结构或优化策略的,这类参数叫作超参数(Hyper-Parameter)。
常见的超参数包括:聚类算法中的类别个数、梯度下降法中的步长、正则化项的系数、神经网络的层数、支持向量机中的核函数等。超参数的选取一般都是组合优化问题,很难通过优化算法来自动学习.因此,超参数优化是机器学习的一个经验性很强的技术,通常是按照人的经验设定,或者通过搜索的方法对一组超参数组合进行不断试错调整。
梯度下降法
为了充分利用凸优化中一些高效、成熟的优化方法,比如共轭梯度、拟牛顿法等,很多机器学习方法都倾向于选择合适的模型和损失函数,以构造一个凸函数作为优化目标.但也有很多模型(比如神经网络)的优化目标是非凸的,只能退而求其次找到局部最优解。
在机器学习中,最简单、常用的优化算法就是梯度下降法,即首先初始化参数θ0,然后按下面的迭代公式来计算训练集D 上风险函数的最小值:
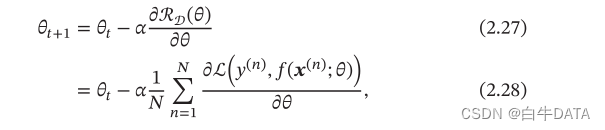
其中θt为第t次迭代时的参数值,α为搜索步长.在机器学习中,α一般称为学习率(Learning Rate)。
提前停止
针对梯度下降的优化算法,除了加正则化项之外,还可以通过提前停止来防止过拟合。
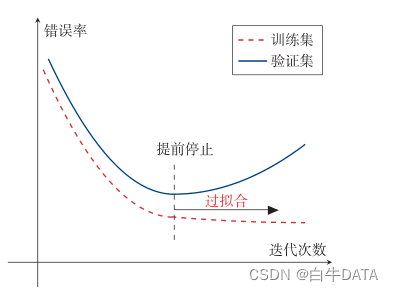
在梯度下降训练的过程中,由于过拟合的原因,在训练样本上收敛的参数,并不一定在测试集上最优。因此,除了训练集和测试集之外,有时也会使用一个验证集(Validation Set)来进行模型选择,测试模型在验证集上是否最优。在每次迭代时,把新得到的模型 𝑓(x;θ) 在验证集上进行测试,并计算错误率。如果在验证集上的错误率不再下降,就停止迭代,这种策略叫提前停止。如果没有验证集,可以在训练集上划分出一个小比例的子集作为验证集。图中给出了提前停止的示例。
随机梯度下降法
在公式 (2.27)的梯度下降法中,目标函数是整个训练集上的风险函数,这种方式称为批量梯度下降法.批量梯度下降法在每次迭代时需要计算每个样本上损失函数的梯度并求和。当训练集中的样本数量N 很大时,空间复杂度比较高,每次迭代的计算开销也很大。
在机器学习中,我们假设每个样本都是独立同分布地从真实数据分布中随机抽取出来的,真正的优化目标是期望风险最小。批量梯度下降法相当于是从真实数据分布中采集 N个样本,并由它们计算出来的经验风险的梯度来近似期望风险的梯度。为了减少每次迭代的计算复杂度,我们也可以在每次迭代时只采集一个样本,计算这个样本损失函数的梯度并更新参数,即随机梯度下降法。当经过足够次数的迭代时,随机梯度下降也可以收敛到局部最优解。
随机梯度下降法的训练过程如算法2.1所示.

批量梯度下降和随机梯度下降之间的区别在于,每次迭代的优化目标是对所有样本的平均损失函数还是对单个样本的损失函数。由于随机梯度下降实现简单,收敛速度也非常快,因此使用非常广泛。机梯度下降相当于在批量梯度下降的梯度上引入了随机噪声。在非凸优化问题中,随机梯度下降更容易逃离局部最优点。
小批量梯度下降法
随机梯度下降法的一个缺点是无法充分利用计算机的并行计算能力。小批量梯度下降法是批量梯度下降和随机梯度下降的折中.每次迭代时,我们随机选取一小部分训练样本来计算梯度并更新参数,这样既可以兼顾随机梯度下降法的优点,也可以提高训练效率。
第t次迭代时,随机选取一个包含K个样本的子集St,计算这个子集上每个样本损失函数的梯度并进行平均,然后再进行参数更新:
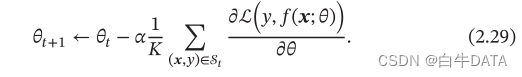
在实际应用中,小批量随机梯度下降法有收敛快、计算开销小的优点,因此逐渐成为大规模的机器学习中的主要优化算法。