堆与二叉树（上）

本篇主要讲的是一些概念，推论和堆的实现（核心在堆的实现这一块）

涉及到的一些结论，证明放到最后，可以选择跳过，知识点过多，当复习一用差不多，如果是刚学这一块的，建议打勾的概念多留意，推论前三个相似，了解其中一个即可，重点看推论四（主要是和堆的实现有关），一定要动手实现堆排序哦，希望对你们有帮助

讲堆之前我们先介绍一下树的概念

一 . 树的概念

什么是树？

树是一种非线性的数据结构，它是由n（n>=0）个有限结点组成一个具有层次关系的集合。它的结构很像一棵倒过来的树

正因为这一点，有些结构的名称就可以跟数联系起来

其中一个特殊的节点叫作根节点，它没有前驱结点
除根节点以外，其余若干个集合叫作子树（子树之间不能相交）
除根节点以外，每个父节点都有一个前驱结点

错误的图示

树的相关知识

图例：

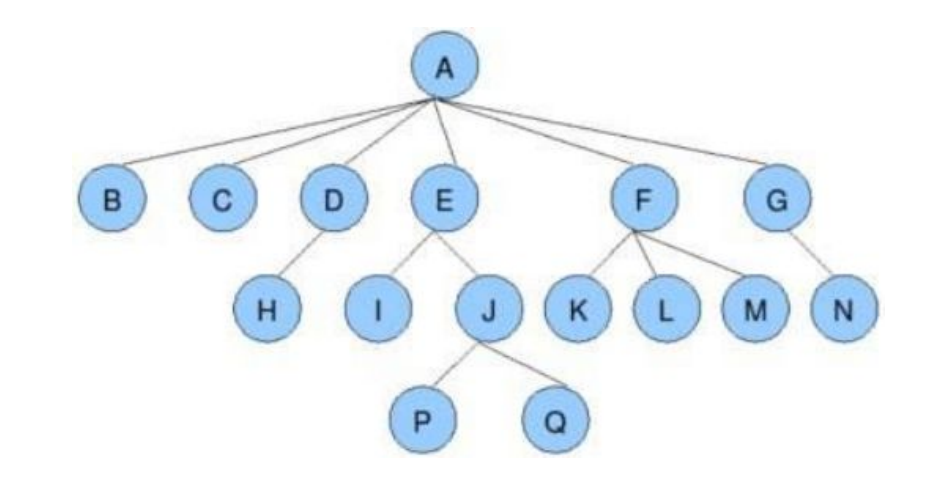
✔节点的度：一个节点含有的子树的个数称为该节点的度；如上图：A的为6

叶节点或终端节点：度为0的节点称为叶节点；如上图：B、C、H、I...等节点为叶节点

非终端节点或分支节点：度不为0的节点；如上图：D、E、F、G...等节点为分支节点

✔双亲节点或父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点；如上图：A是B的父节点 (注：A不仅是根节点，也是父节点)

✔孩子节点或子节点：一个节点含有的子树的根节点称为该节点的子节点；如上图：B是A的孩子节点

兄弟节点：具有相同父节点的节点互称为兄弟节点；如上图：B、C是兄弟节点

树的度：一棵树中，最大的节点的度称为树的度；如上图：树的度为6

节点的层次：从根开始定义起，根为第1层，根的子节点为第2层，以此类推

✔树的高度或深度：树中节点的最大层次；如上图：树的高度为4

堂兄弟节点：双亲在同一层的节点互为堂兄弟；如上图：H、I互为兄弟节点

节点的祖先：从根到该节点所经分支上的所有节点；如上图：A是所有节点的祖先

子孙：以某节点为根的子树中任一节点都称为该节点的子孙。如上图：所有节点都是A的子孙

森林：由m（m>0）棵互不相交的树的集合称为森林；

二. 二叉树

二叉树的概念

二叉树是一种特殊的树

每个父节点都最多有两个子节点

图例1

特殊的二叉树

满二叉树

要求每一个父节点必须有两个子节点（如上述图例1）

2. 完全二叉树

要求节点是连续存放的

（这里用数组的存储形式来说明）

正确示范：

错误示范：

二叉树的一些推论

规定根节点的层数为 1 ，总层数为 h ,节点个数为 n

推论1

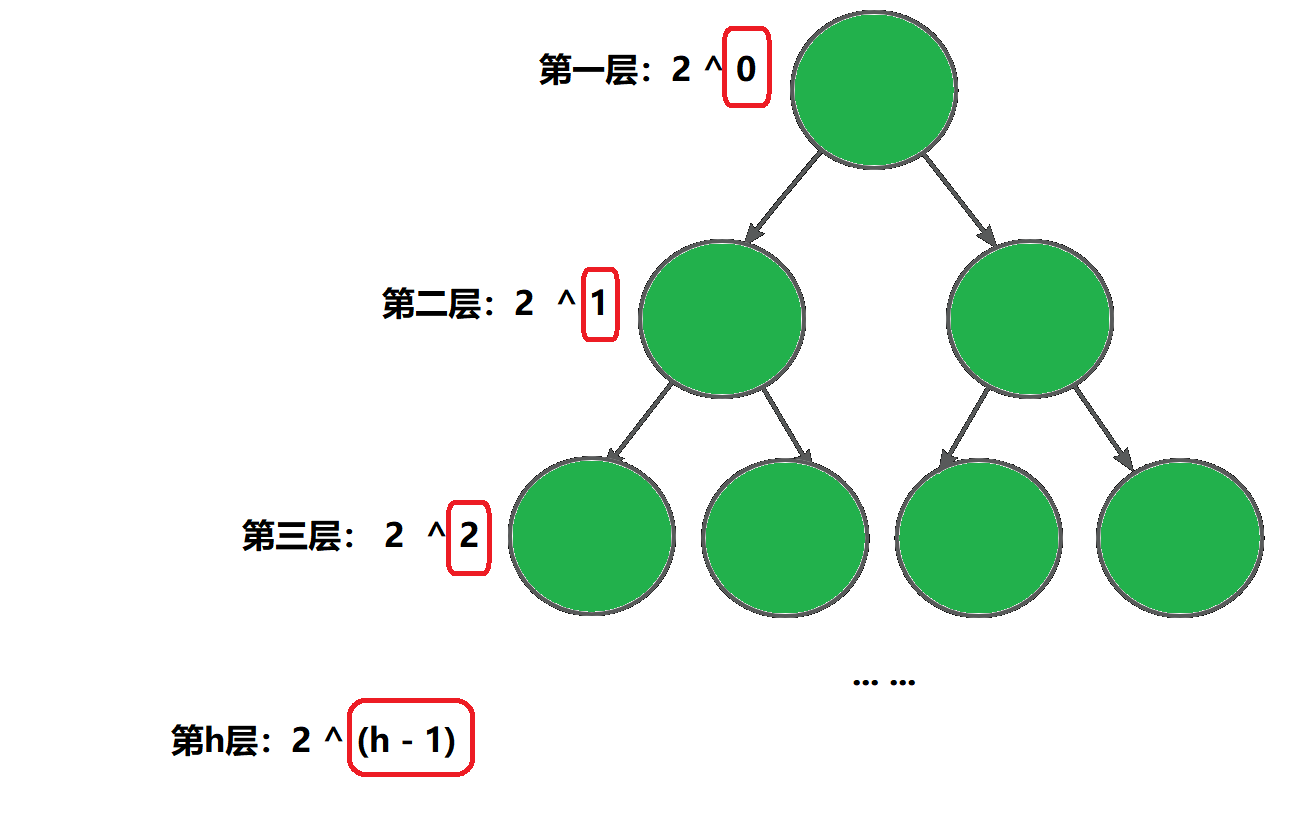
已知总层数为 h，求最后一层的节点个数的最大值：

2 ^（h - 1）

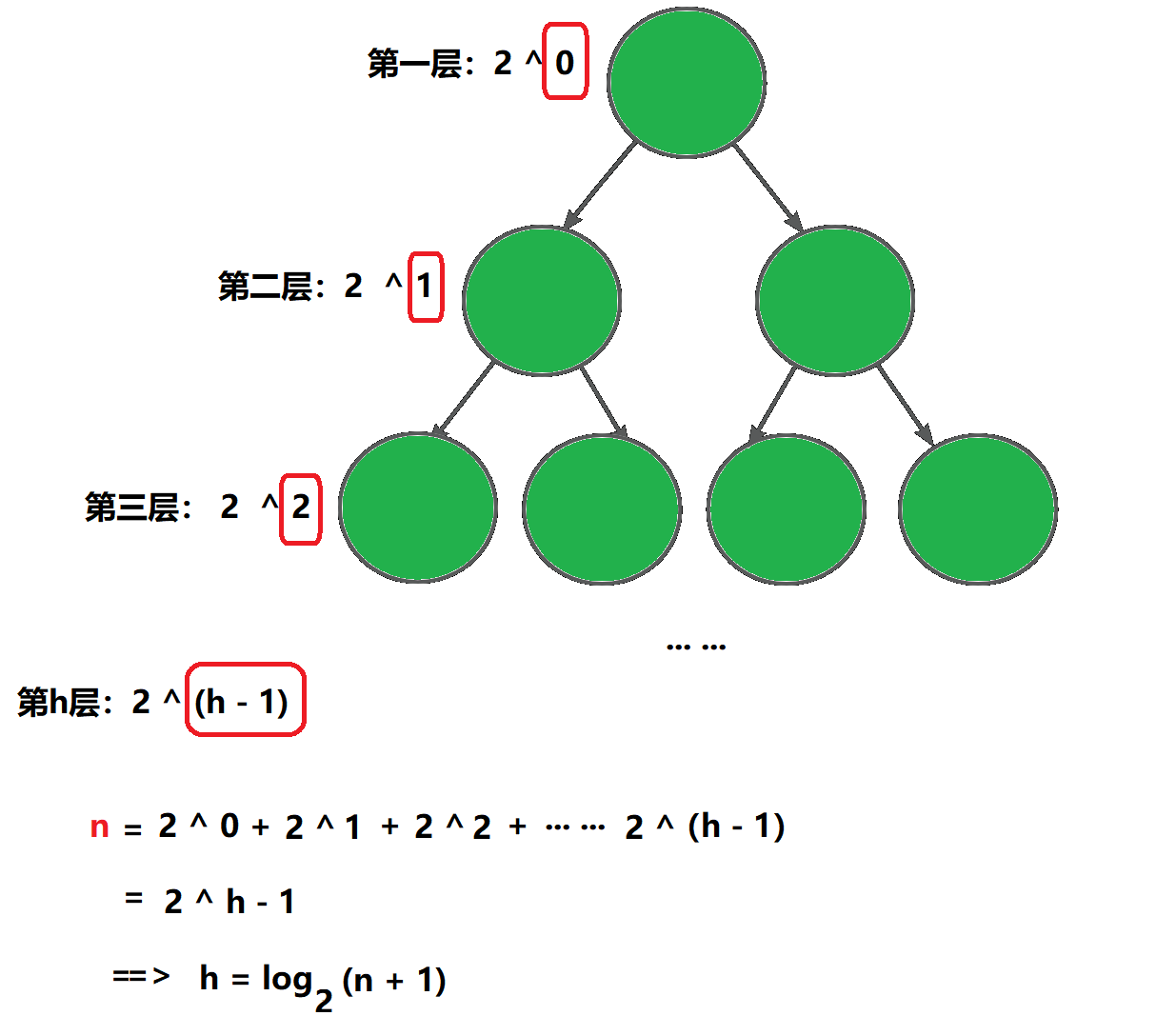
推论2

已知节点个数为 n，求具有n个结点的满二叉树的深度 h

推论3

若根节点层数为1（保证不是空树），已知深度为 h ,则求二叉树的最大节点数：

推论4

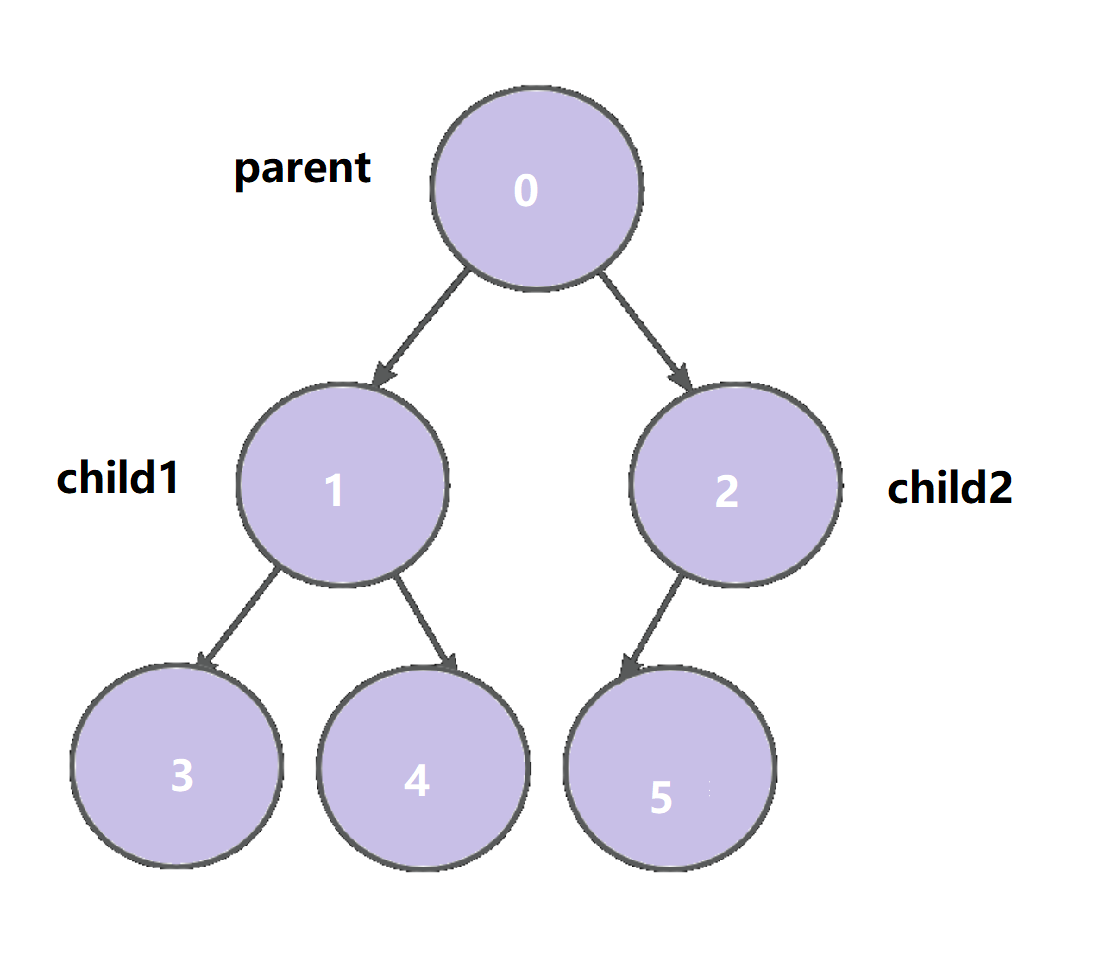
已经节点总个数 n 的完全二叉树，从第一个根节点开始以 0 编号，从左到右，从上到下编号依次增加 1

求父节点和左右孩子节点的关系(parent , child 1 和 child2 都是下标)

a. 若知道 parent：

则 child1 = parent * 2 + 1

child2 = parent * 2 + 2

b. 若知道 child (无论哪个孩子下标都可以)：

则 parent = (child - 1) / 2

推论5

对任何一棵二叉树, 如果度为0其叶结点个数为 n0 , 度为2的分支结点个数为 n2 ,

则有 n0 ＝ n2 ＋1

证明推论5

用图例阐明遇到的情况：

我们发现当 n1 + 1 ，意味着 n0 - 1

n2 + 1 , 意味着 n1 - 1

证明推论1

证明推论2

证明推论3

是推论2

(即是满二叉树)

证明推论4

完全二叉树有一个性质，它是连续存放的

第一个结论通过画图我们很容易就得到了

第二个结论主要注意的是：

由于下标都是 int 类型的，最终得到的一定是整数

证明推论5

用图例阐明遇到的情况：

我们发现当 n1 + 1 ，意味着 n0 - 1

n2 + 1 , 意味着 n1 - 1

三 . 二叉树的储存结构

二叉树有两种储存形式：

一个是 顺序储存结构 ，另一个是 链式储存结构

顺序结构存储就是使用数组来存储，一般使用数组只适合表示完全二叉树，因为不是完全二叉树就会有空间的浪费

图例

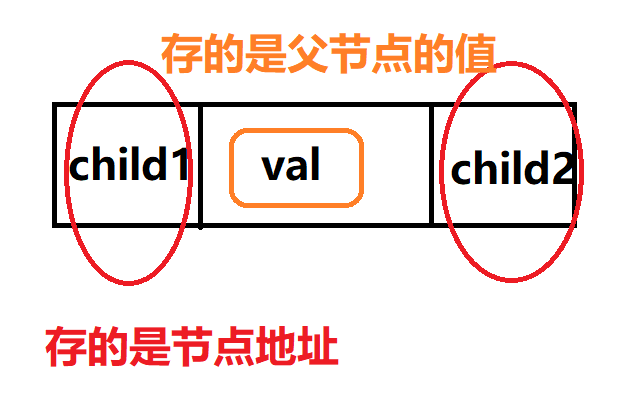
2. 二叉树的链式存储结构是指，用链表来表示一棵二叉树，

一般两个指针存放左右孩子的节点

图例

四 . 堆的概念

堆的性质

堆满足以下性质：

是一棵完全二叉树
只有小堆或者大堆

（小堆：父节点的值永远小于等于两个孩子节点的值；

大堆：父节点的值永远大于等于两个孩子节点的值）

图例

堆的实现

1. 堆的排序

堆的排序有两种：向上排序法和向下排序法（这里用顺序结构）

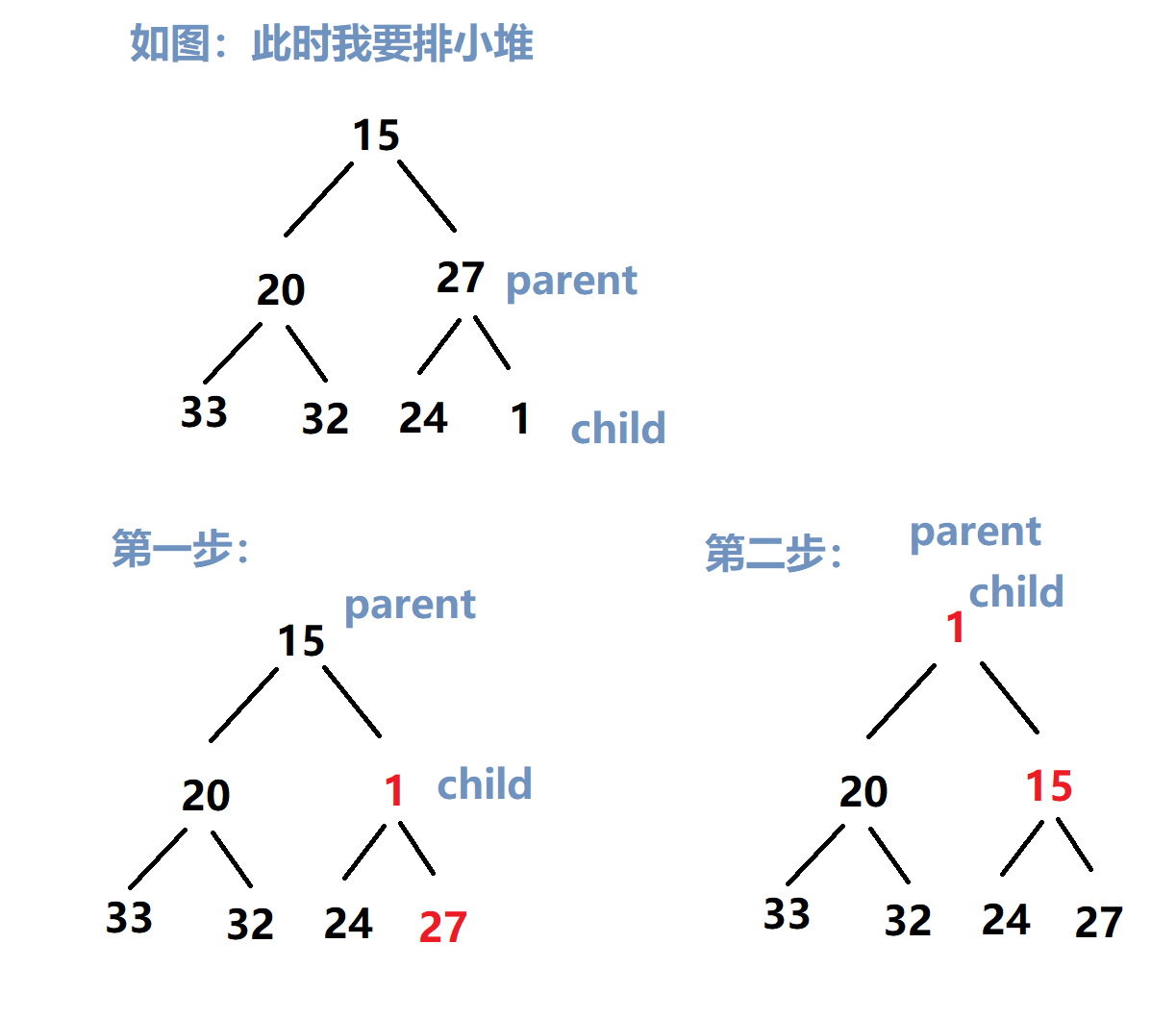
向上排序法

该方法可以在一个个把数值放进去的同时进行排序

实现思路如下：

父节点下标从 0 开始，一个节点也是一个堆（所以放入第一个数的时候是不用进行排序的），后面的数先把值放入数组，再进行与父节点进行对比（已知 child 下标，求 parent 下标，回到推论4）

[由于可能发生多次交换问题，这里需要用到循环]

如果父节点的值大于子节点的值（排小堆），则交换；

如果父节点的值小于子节点的值（排大堆），则交换.

并且此时 child 下标和 parent 下标都要发生改变，让上一个父节点和上一个子节点作比较

注意：想要改变两个值，一定要传地址

结束条件：

如果不用交换可以跳出循环

或者到 child > 0 时，跳出循环

代码

void swap(int* p1, int* p2)
{
	if (*p1 == *p2)
	{
		return;
	}
	else
	{
		int tmp = *p1;
		*p1 = *p2;
		*p2 = tmp;
	}
}
void upAdjust(int* pa, int n)
{
	for (int i = 1; i < n; i++)
	{
		int child = i;
		int parent = (child - 1) / 2;
		while (child > 0)
		{
			if (pa[parent] > pa[child])
			{
				swap(&pa[parent], &pa[child]);
				child = parent;
				parent = (child - 1) / 2;
			}
			else
			{
				break;
			}
		}
	}

}

向下排序法

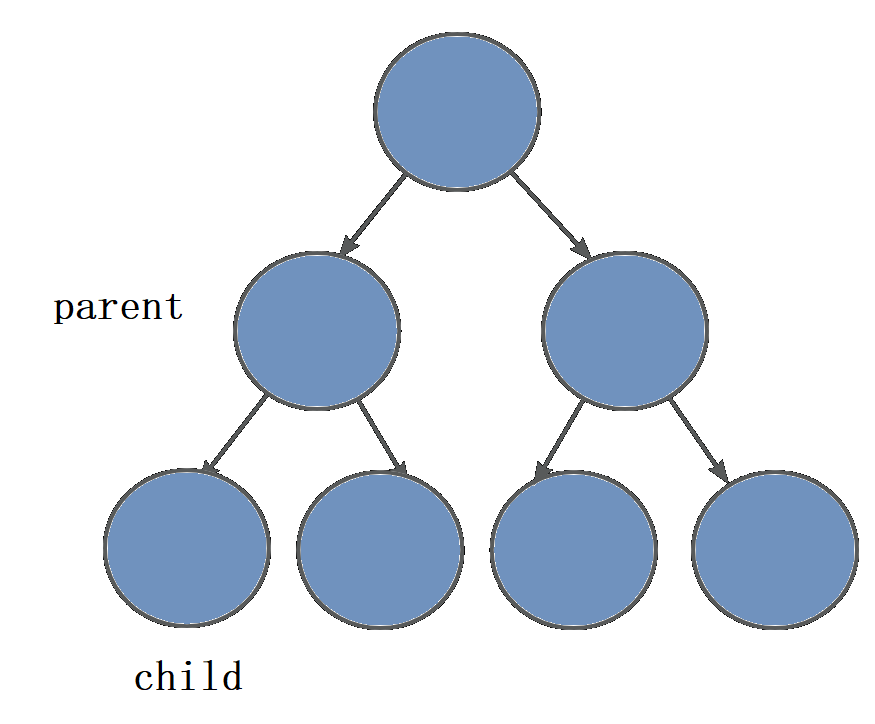
给一组无序数组，我们给它排序，这里需要我们从最后一棵子树（度不为0）的父节点和它的子节点开始倒着排序

像这样：

我们以第一棵树为例（序号为1的树）

这里更容易找到子节点，然后根据公式推出父节点

但是我们的思路是让父节点与 （更小的）子节点比较（小堆），或者与（更大的）子节点比较 (大堆)

这里的子节点需要通过比较确定，所以我们先去找父节点的下标起

parent = (n - 1) / 2

child = parent * 2 + 1(假设第一个节点就是我们需要比较的那个节点)

再与第二个节点进行对比，确定 child 下标（判断时为了防止没有第二个子节点而越界的情况，一定要对其进行判断）

对比父节点和子节点的值

我们还需要向下调整

此时 parent = child

child = parent * 2 + 1

一直到 child >= n (这是最内层的循环结束条件)

比完第一棵树，再比第二棵树

此时 parent -= 1 (完全二叉树是连续的)

注意：由于可能发生连续向下的调整，导致 parent 的值会发生改变，所以我们需要得到第一棵树最开始的 parent

child = parent * 2 + 1

重复上述动作，直到

parent >= 0（这是最外层的循环条件）

代码

void swap(int* p1, int* p2)
{
	if (*p1 == *p2)
	{
		return;
	}
	else
	{
		int tmp = *p1;
		*p1 = *p2;
		*p2 = tmp;
	}
}
void downAdjust(int* pa, int parent, int n)
{
	int child = parent * 2 + 1;
	while (child < n)
	{
		if (child + 1 < n && pa[child] > pa[child + 1])
		{
			child++;
		}
		if (pa[parent] > pa[child])
		{
			swap(&pa[parent], &pa[child]);
		}
		parent = child;
		child = parent * 2 + 1;
        else
        {
	        break;
        }
	}
}
for (int i = (n - 1 - 1) / 2; i >= 0; i--)
{
	downAdjust(arr,i,n);
}

2. 实现堆

堆的实现分几步：（这里用顺序结构）

堆的步骤

a. 构造一个堆的结构体

结构体成员：

存放整型数组的指针 : int *a

整个数组的元素个数 : int size

整个数组的的容量 : int capacity

b. 初始化结构体

size = 0

让 a 动态开辟 4 * sizeof(int) 个字节

capacity = 4

c. 放入元素

创建一个自定义函数放入元素

注意：

若 size ==capacity，开辟 sizeof( int ) * capacity * 2 的字节

capacity = capacity * 2

先一个个从插入元素，再进行调整（这里我们用向上调整法）

size++

d. 判断是否为空

创建一个自定义函数，判断数组里面是否还有元素很简单，只要判断

size == 0 即可

e. 删除元素（这里我们的删除一定是删除根节点的值）

创建一个自定义函数删除元素

删除元素第一步是一定要判断是否为空

为了继续维护堆，我们需要一个元素覆盖根节点的值，从而抹去这个值，但是如果根节点与它的子节点直接进行覆盖，会破坏之前的大堆（或小堆）

所以我们的办法是：

把根节点的值与最后一个值交换（保证其它的父子关系不变）

size--

我们再使用向下调整法

f. 打印堆

g. 释放堆的空间

代码

#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
typedef struct HeapList
{
	int* a;
	int size;
	int capacity;
}HP;
void InitHeap(HP *heap)
{
	int* pa = (int*)malloc(sizeof(int) *  4);
	if (pa == NULL)
	{
		perror("realloc");
		return;
	}
	heap->a = pa;
	heap->capacity = 4;
	heap->size = 0;
}
void swap(int* p1, int* p2)
{
	if (*p1 == *p2)
	{
		return;
	}
	else
	{
		int tmp = *p1;
		*p1 = *p2;
		*p2 = tmp;
	}
}
void upAdjust(int* pa, int n)
{
	for (int i = 1; i < n; i++)
	{
		int child = i;
		int parent = (child - 1) / 2;
		while (child > 0)
		{
			if (pa[parent] > pa[child])
			{
				swap(&pa[parent], &pa[child]);
				child = parent;
				parent = (child - 1) / 2;
			}
			else
			{
				break;
			}
		}
	}

}
void downAdjust(int* pa, int parent, int n)
{
	int child = parent * 2 + 1;
	while (child < n)
	{
		if (child + 1 < n && pa[child] > pa[child + 1])
		{
			child++;
		}
		if (pa[parent] > pa[child])
		{
			swap(&pa[parent], &pa[child]);
		}
		parent = child;
		child = parent * 2 + 1;
	}
}
void HeapPush(HP* heap ,int x)
{
	if (heap->size == heap->capacity)
	{
		int* pa = (int*)realloc(heap->a, sizeof(int) * heap->capacity * 2);
		if (pa == NULL)
		{
			perror("realloc");
			return;
		}
		heap->a = pa;
		heap->capacity = heap->capacity * 2;
	}
	heap->a[heap->size] = x;
	heap->size++;
	upAdjust(heap->a, heap->size);
}
bool IsEmpty(HP* heap)
{
	return heap->size == 0;
}
void HeapPop(HP* heap)
{
	assert(!IsEmpty(heap));
	swap(&heap->a[0], &heap->a[heap->size - 1]);
	heap->size--;
	downAdjust(heap->a, 0, heap->size);
}
void PrintHeap(HP* heap)
{
	for (int i = 0; i < heap->size; i++)
	{
		printf("%d ", heap->a[i]);
	}
	printf("\n");
}
void DestoryHeap(HP* heap)
{
	free(heap->a);
	heap->a = NULL;
	heap->size = heap->capacity = 0;
}