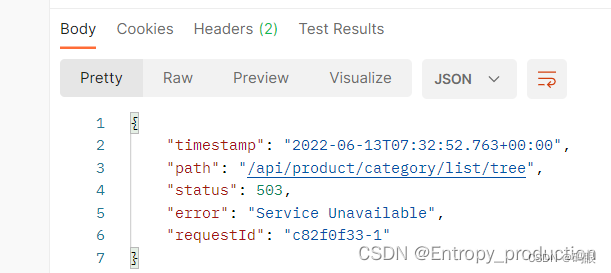
跳跃表的基本内容:
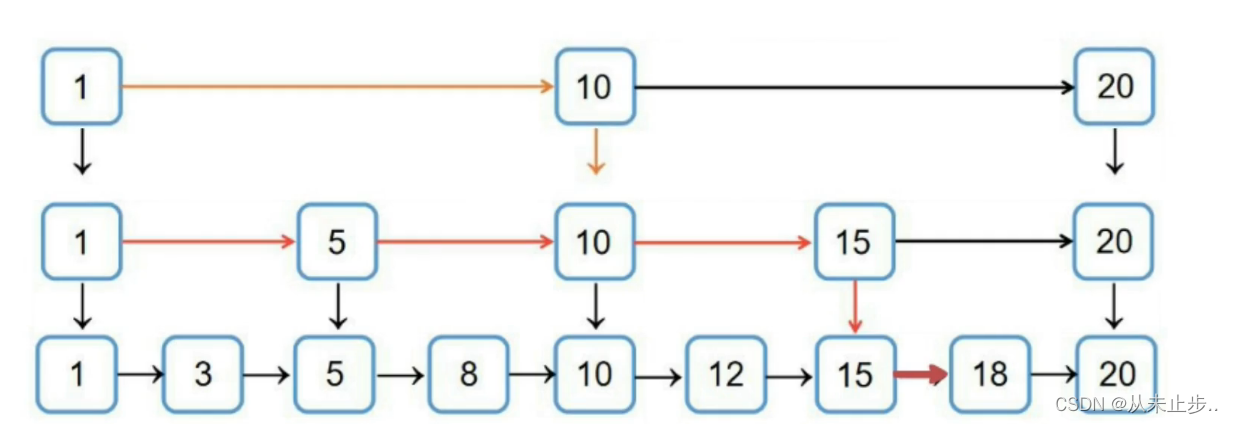
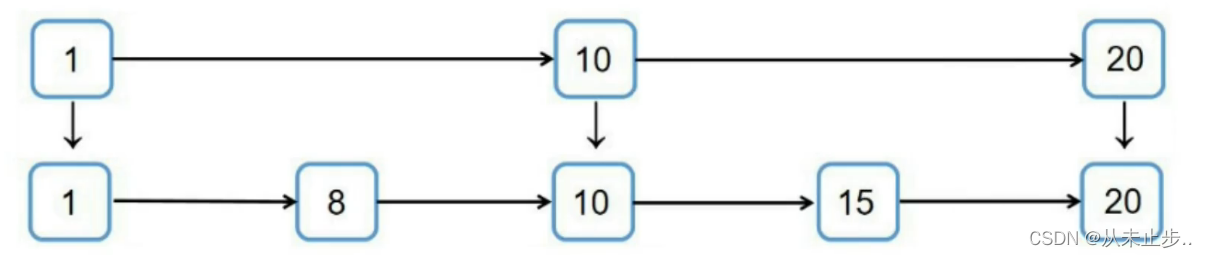
对于一个有序序列,链表相对于数组来说,删除和插入的效率要快很多,只需要改变指针的指向,但是在查找的时候,数组就要更占优势一些,可以随机访问,然而链表需要从头开始遍历,最坏的情况下可能达到了O(n),为了改变链表的这一弊端,人们就想出了利用空间换时间的策略,尝试给链表加个索引,假设我们当前有如下所示的普通链表:
我们要查找18需要比较8次

但如果如下所示我们给当前链表添加一层索引,那么只需要比较5次

如果我们给当前链表添加两层索引(如下所示),那么只需要比较4次
跳表的第一层存储的是所有的元素,每个节点存在两个指针,指向后继节点和下一层的节点,查找的时候从最高层开始,逐层比较直到第一层
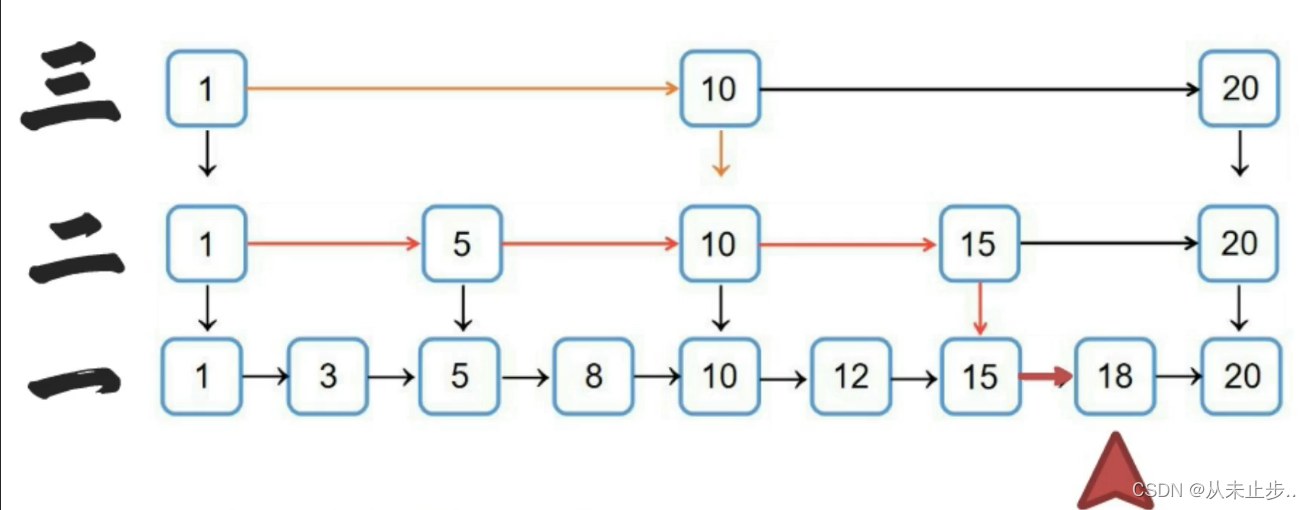
对于跳跃表来说,假设我们现在想要插入数据,我们不但要在链表中插入数据,还要去更新索引,如果直接插入数据而不更新索引,那么很有可能出现两个索引之间存在大量的数据,同时也失去了创建索引的意义,那么要如何更新索引呢?
上层节点个数应该是下层节点个数的二分之一,因此我们希望这个新节点添加到上一层的概率是二分之一,最简单的方式就是抛硬币,因为正反面的概率都是二分之一,所以我们只要让它在0和1之间随机,如果是0就停止,如果是1就继续,最后出现的次数k,就代表我们需要在第一层到第k层之间添加索引,当然我们也不能让它无限增长,所以我们还需要添加一个最大值的限制
public int getRandom(){
int k=1;
Random random=new Random();
//random.nextBoolean()返回一个随机的 boolean 值,即 true 或 false
while(random.nextBoolean()&&k<MAX_VALUE){
k++;
}
return k;
}
跳跃表的增删改查:
比如我们添加一个节点为13,随机值为2
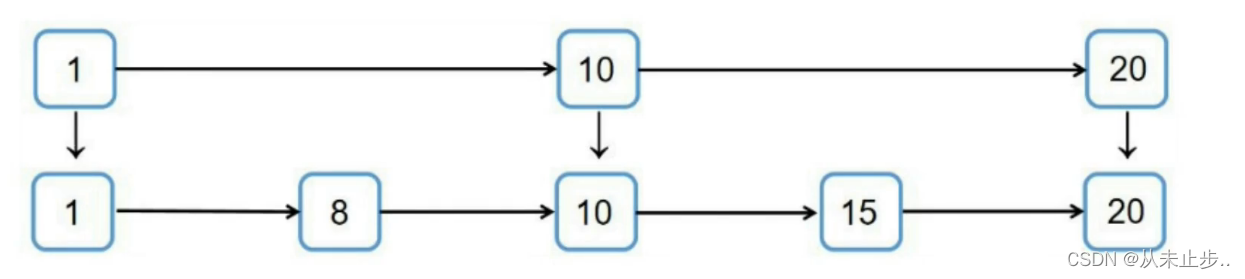
那么我们只需要在第一层和第二层加入13即可
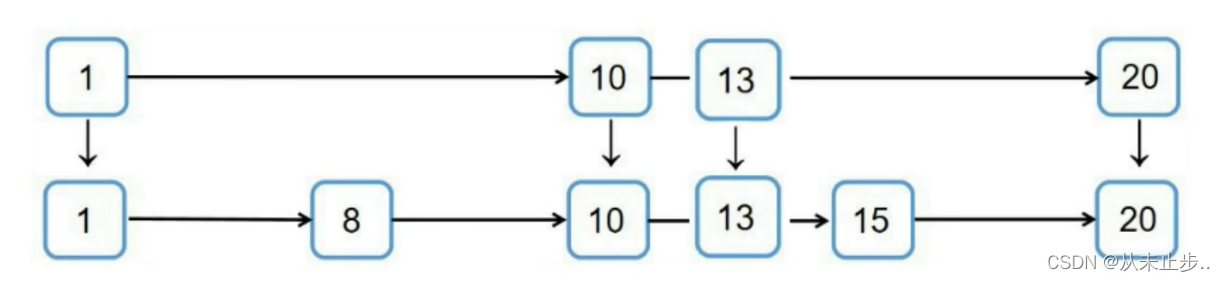
删除操作就比较简单了,直接将我们节点和跨越的层数删除即可
时间复杂度:
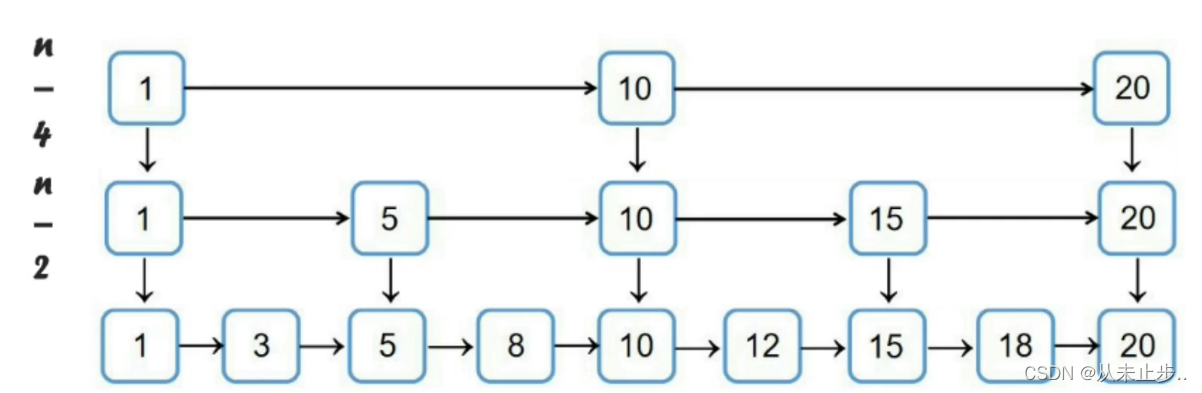
第一层的索引节点数为n个,第二层为n/2个,那么第K层的索引节点数为
注意:当某层的索引节点只有两个时,我们就不增加索引了
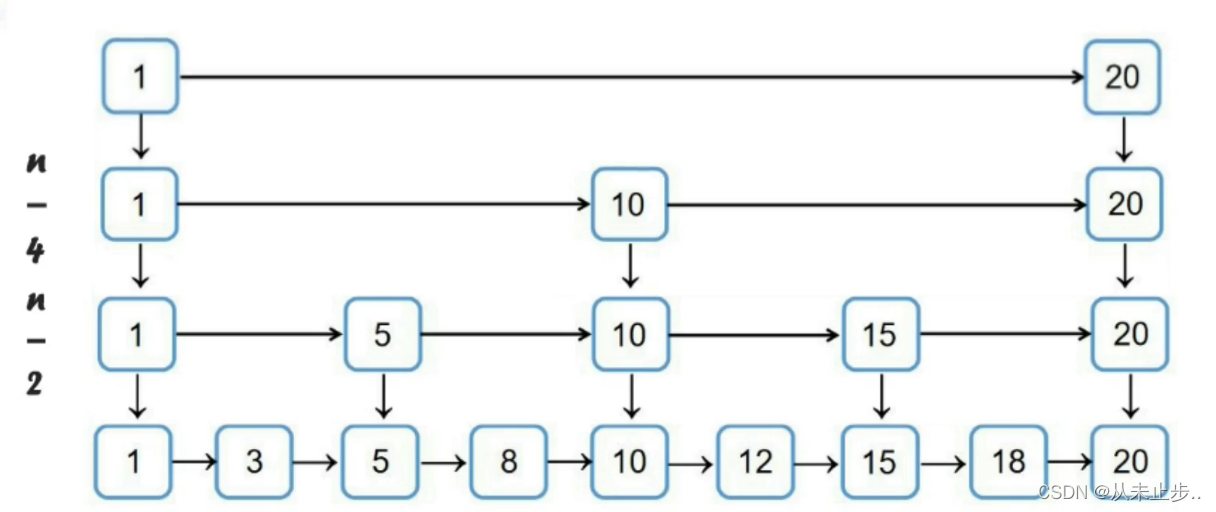
下述中的2为当索引个数为2时,我们就不再添加索引了,h为跳跃表的高度
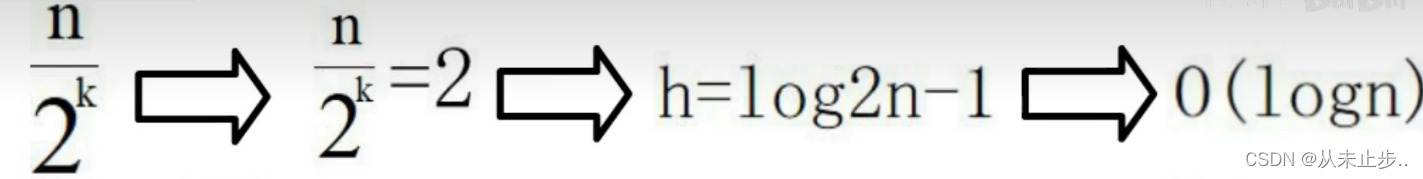
如果我们每一层要遍历X个节点,那么在跳表中查找的时间复杂度就为O(Xlogn),可认为O(logn)
由于插入和删除的时间复杂度都是O(1),时间主要花费在查找元素的位置,所以插入和删除的时间复杂度都为O(logn)