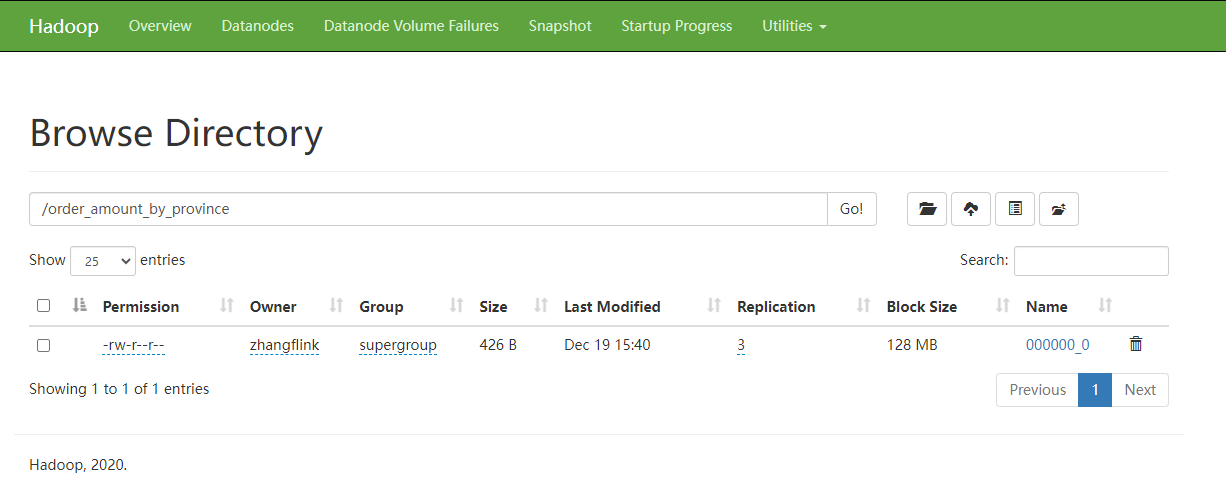
目录
1 什么是激活函数? activation function
1.1 阈值
1.2 激活函数a(x) ,包含偏置值θ
1.3 激活函数a(x) ,包含偏置值b
2 激活函数1: 单位阶跃函数
2.1 函数形式
2.2 函数图形
2.3 函数特点
2.4 代码实现这个 单位阶跃函数
3 激活函数2 sigmoid函数
3.1 函数形式
3.2 函数图形
3.3 函数特点
3.3.1 是一个连续函数,且是一个渐变的曲线
3.3.2 是连续区间的[0,1] , 可以天然等价视为概率!
3.3.3 计算方便,求导数方便,
3.4 代码实现
3.4.1 sigmoid函数的实现,和 跃迁函数 对比
3.4.2 容易犯的错误
3.4.3 标准函数代码写法
1 什么是激活函数? activation function
一般是神经网络/ 感知机 用到的判断 神经元是否被激活的函数
1.1 阈值
- 阈值判断
- 阈值θ 太高神经容易被激活,很容易兴奋
- 阈值θ 太低神经不容易被激活,不够敏感
- if/当 w1x1+w2x2+w3x3+.....<θ 不能激活
- if/当 w1x1+w2x2+w3x3+.....>=θ 才能激活
- 因此 w1x1+w2x2+w3x3+.....=θ 时,就是刚好可以激活的阈值
1.2 激活函数a(x) ,包含偏置值θ
- y=a(w1x1+w2x2+w3x3+.....-θ)
- y=a(w,x,θ)
- x 是输入的多个信息,w是每个信息的权重,θ是判断是否激活的阈值
- a(x) 就是激活函数
1.3 激活函数a(x) ,包含偏置值b
- y=a(w1x1+w2x2+w3x3+.....+b)
- θ是判断是否激活的阈值 变成了偏置值b
2 激活函数1: 单位阶跃函数
2.1 函数形式
函数形式 y=f(x)
- 可以说是 分段函数,或 阶跃函数/单位阶跃函数
- f(x)=0, if x<0
- f(x)=1, if x>=0
2.2 函数图形
- 从图形上看,
- 可以说是 分段函数
- 或 阶跃函数/单位阶跃函数

2.3 函数特点
- 设置函数的结果在0-1之间,
- 天生的符合概率的[0,1] 设计
- 一个最简单的函数,分段函数图形是直的,但是上下限也是[0,1]
2.4 代码实现这个 单位阶跃函数
import numpy as np
import matplotlib.pyplot as plt
plt.figure()
X=np.linspace(-5,5,100)
Y=[]
for x in X:
if x<0:
y=-1
Y.append(y)
elif x>=0:
y=1
Y.append(y)
plt.plot(X,Y)
plt.show
3 激活函数2 sigmoid函数
sigmod函数比较经典
3.1 函数形式
- sigmod函数形式,y=f(x)
- f(x)=1/(1+e^(-x))
- f(x)=1/(1+np.exp(-X)) #python内调用 numpy写法
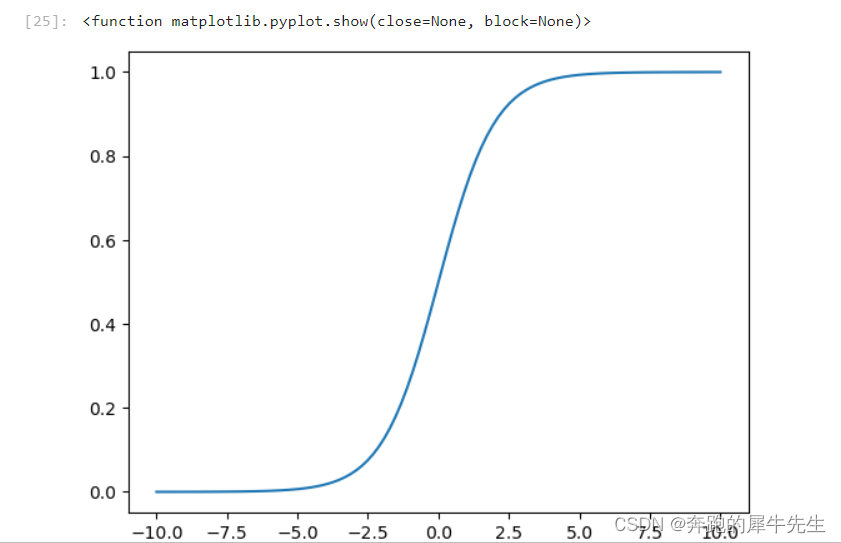
3.2 函数图形
- 函数图形是连续的
- 函数的范围是[0,1]
- 完全可以假设看作一种概率分布曲线pdf
3.3 函数特点
3.3.1 是一个连续函数,且是一个渐变的曲线
- 一个比较连续的
- sigmod函数图形是曲线
3.3.2 是连续区间的[0,1] , 可以天然等价视为概率!
- 上下限也是[0,1]
- 并且在[0,1] 上是连续的,可以天然视为概率
3.3.3 计算方便,求导数方便,
- 其中 (e^(-x))' = -e^(-x) ,可以通过复合函数求导推出
- 为了不同情况下计算方便
- 因为 e^(-x)' =
- f(x)=1/(1+e^(-x))
3.4 代码实现
3.4.1 sigmoid函数的实现,和 跃迁函数 对比
import numpy as np
import matplotlib.pyplot as plt
plt.figure()
X=np.linspace(-5,5,100)
Y=[]
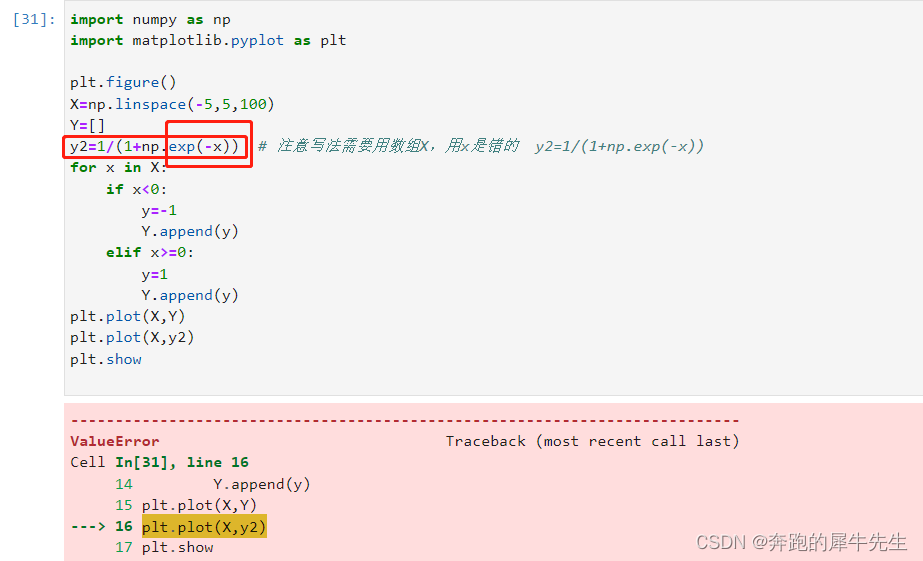
y2=1/(1+np.exp(-X)) # 注意写法需要用数组X,用x是错的 y2=1/(1+np.exp(-x))
for x in X:
if x<0:
y=-1
Y.append(y)
elif x>=0:
y=1
Y.append(y)
plt.plot(X,Y)
plt.plot(X,y2)
plt.show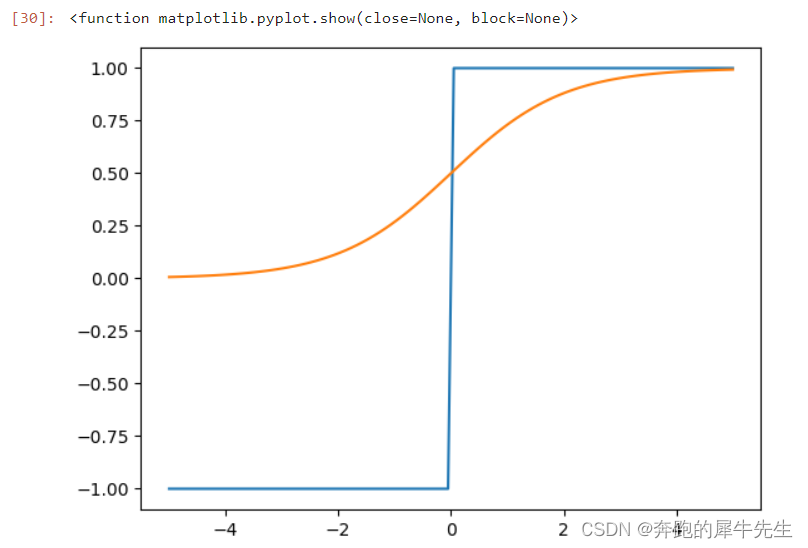
3.4.2 容易犯的错误
-
ValueError: x and y must have same first dimension, but have shapes (100,) and (1,)
- 因为 X是数组,维度是1,而x只是代表数组X里的某个变量,维度是100
- y需要和X对应,而不能和x对应
3.4.3 标准函数代码写法
- 先def sigmoid() 函数,return 1/(1+np.exp(-x))
- 然后y 或者f(x)调用 sigmoid函数
def sigmoid(x):
return 1/(1+np.exp(-x))
plt.figure()
X=np.linspace(-10,10,100)
y2=sigmoid(X)
# y2=1/(1-np.exp(-x)) #这样不行
plt.plot(X,y2)
plt.show
激活函数2,另外一种
还有的函数,分段函数图形是直的,但是上下限也是[-1,1]
f(x)=1, if x>0
f(x)=-1, if x<=0
类似的例子比如
1/2Σi=1~n(Yi-f(x)i)^2 ,加上1/2 就是为了微分结果导数更简单
激活函数3
如果有2个输出结果,就不适合 感知机的模式了?
最原始的
最小二乘法
最小误差之和