二叉树【数据结构】

二叉树
- 1. 二叉树定义
- - 二叉树的存储定义
- 2. 遍历二叉树
- - (1) 前序遍历
  - (2) 中序遍历
  - (3) 后序遍历
  - (4) 层序遍历
- 3. 二叉树的相关操作
- - (1) 二叉树的初始化
  - (2) 二叉树的结点的手动创建
  - (3) 二叉树结点的个数
  - (4) 二叉树叶子结点的个数
  - (5) 二叉树的高度
  - (6) 第k层结点个数
  - (7) 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
  - (8) 二叉树查找值为x的结点
  - (9) 判断是否为完全二叉树
  - (10) 二叉树的销毁

前言：
之前讲到过：
数据结构：是存在一种或多种特定关系的数据元素的集合。其中，一种或多种特定关系，会分为：逻辑结构和物理结构(也叫存储结构)。

逻辑结构：数据对象中数据元素之间的相互关系。其中逻辑结构又分为多种
- 集合结构：集合结构中的元素属于同集合，没有其他关系
- 线性结构：数据元素之间是一对一的关系
- 树形结构：数据元素之间是一对多的层次关系
- 图形结构：数据元素之间是多对多的的关系

物理(存储)结构：

线性(顺序)存储
链式存储

首先简单滴介绍一下树

树：是一种对多的层次关系
树是一种非线性的数据结构，由节点（或称为顶点）和边组成。它可以表示为一个层次结构，其中每个节点都可以有零个或多个子节点。树的一个节点称为其父节点的子节点，而父节点则称为其子节点的父节点。树的顶部节点称为根节点，没有父节点的节点称为叶节点。树可以用于表示层次关系，如文件系统的目录结构或组织结构图。
在这里插入图片描述
关于结点的分类：

结点的度：结点拥有的子树
叶子结点：度为0的结点
分支结点：度不为0的结点
树的度：分支结点度的最大值

二叉树

1. 二叉树定义

二叉树定义：由一个根结点和两棵互不相交、分别称为根结点的左右子树的二叉树组成
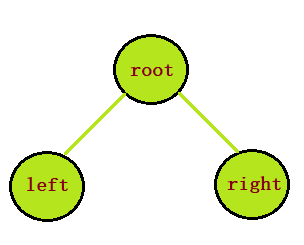
在这里插入图片描述
二叉树的特点：

每个结点最多有两棵子树，所以二叉树中不存在度大于2的结点
左右子树是有顺序的不能颠倒

二叉树的基本形态：

空二叉树
只有一个根结点
根节点只有左子树
根结点只有左子树
根结点既有左子树又有右子树

在这里插入图片描述
满二叉树: 在一棵二叉树中，所有分支结点都存在左子树和右子树，并且所有叶子都在同一层上
满二叉树的特点：

叶子结点只能出现在最下一层
分叶子结点的度一定是2
在相同深度的二叉树中，满二叉树的结点个数最多，叶子树最多

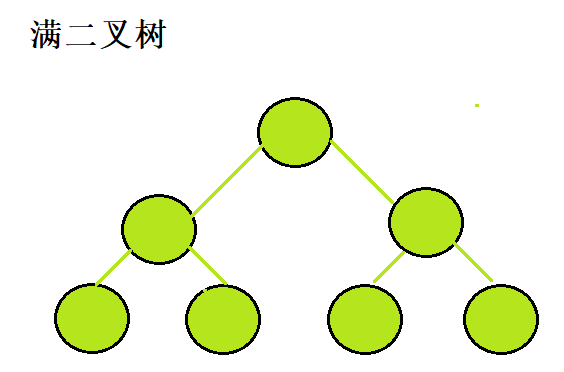
在这里插入图片描述

完全二叉树:
除了最后一层外，也就是前n-1层的结点都必须是满的，最后一层的结点从左到右连续存在，不能有间隔
完全二叉树的特点：

叶子只能出现在最后两层
最后一层从左到有是连续的

二叉树的存储定义

二叉树的顺序存储
二叉树的链式存储

这里我们采用链式存储方式

存储结构:

代码展示

typedef int BTDataType;

typedef struct BinaryTreeNode 
{
	BTDataType val;	//二叉树的值
	struct BinaryTreeNode* left;	//指向左子树
	struct BinaryTreeNode* right;	//指向右子树
}BinaryTree;

2. 遍历二叉树

二叉树遍历：从根结点出发，按某种次序访问二叉树中的所有结点，使得每个结点被访问一次且仅被访问一次

因为我们习惯从左到右的习惯，二叉树的遍历方法分为前序、中序、后序、层序遍历

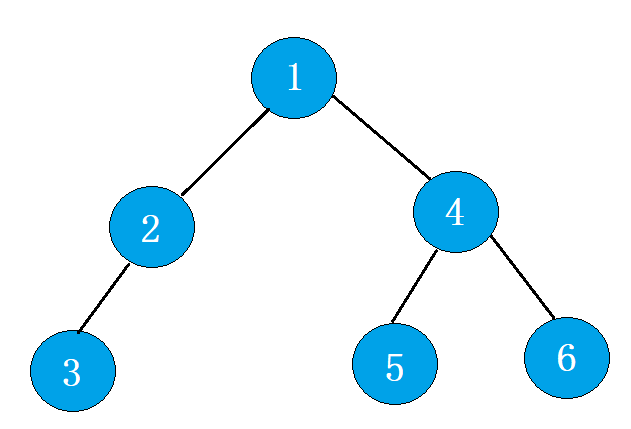
在这里插入图片描述

这里的二叉树的存储结构我们使用链式存储

(1) 前序遍历

前序遍历(先根遍历)：若二叉树为空，返回空，否则访问根结点，然后前序遍历左子树，再前序遍历右子树。

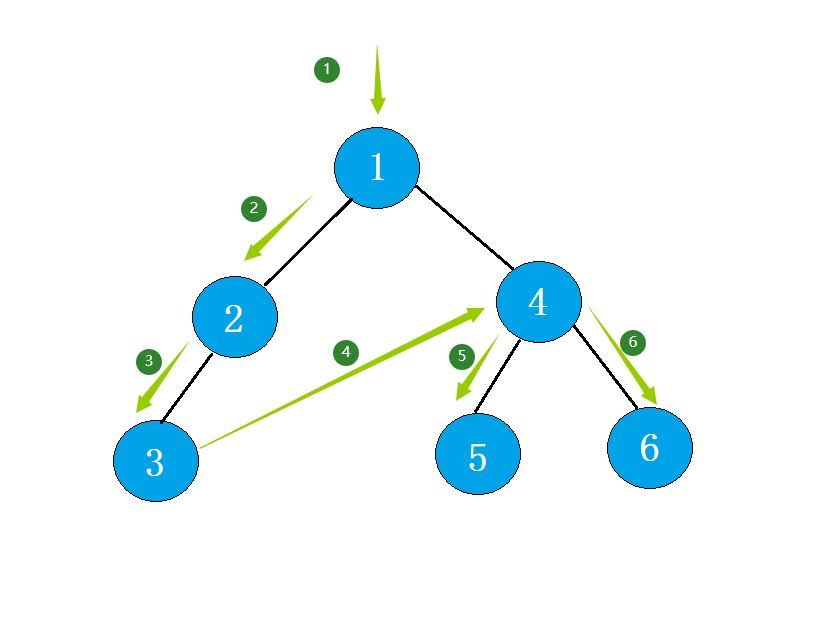
在这里插入图片描述

代码展示

//前序遍历二叉树
void PreOrderTree(BinaryTree* root) 
{
	//如果遇到空打印N 并返回函数调用的地方
	if (root == NULL)
	{
		printf("N ");
		return;
	}
	printf("%d ",root->val);	//打印结点的值
	PreOrderTree(root->left);	//先序遍历左子树
	PreOrderTree(root->right);	//先序遍历右子树
}

如图：
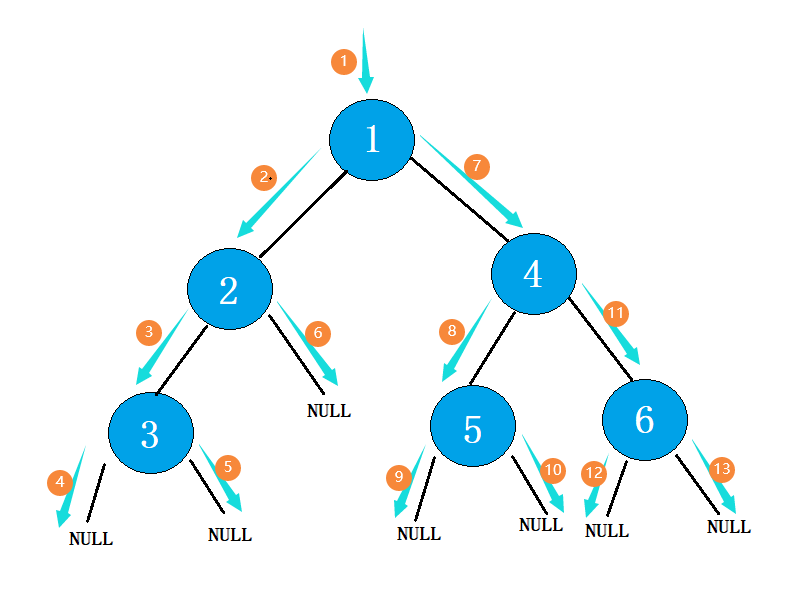
在这里插入图片描述

(2) 中序遍历

中序遍历(中根遍历)：若二叉树为空，返回空，否则中序遍历左子树，再访问根结点，中序遍历右子树。
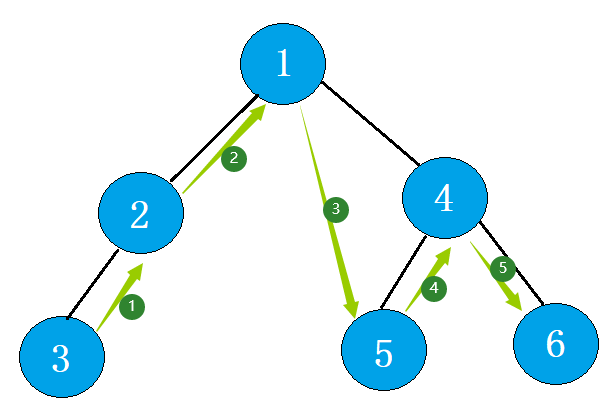
在这里插入图片描述
代码展示

//中序遍历二叉树
void InOrderTree(BinaryTree* root)
{
	//如果遇到空打印N 并返回函数调用的地方
	if (root == NULL)
	{
		printf("N ");
		return;
	}
	InOrderTree(root->left);	//中序遍历左子树
	printf("%d ", root->val);
	InOrderTree(root->right);	//中序遍历右子树
}

(3) 后序遍历

后序遍历(后根遍历)：若二叉树为空，返回空，否则后序遍历左子树 , 后序遍历右子树 , 再访问根结点。

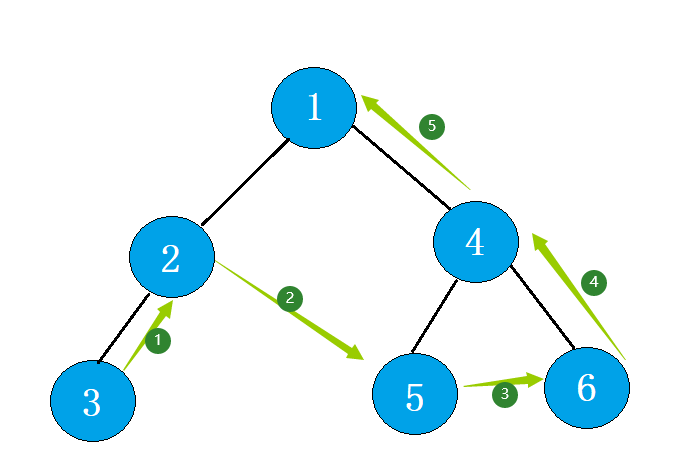
在这里插入图片描述
“#” 表示空

(4) 层序遍历

层序遍历：这里我们需要借助队列来实现，原理：上一层出来会依次带入下一层进入(队列:先进先出)
在这里插入图片描述

思路：

根结点不为空就进队(注意是结点进队，不是结点的值进队)
队头结点进行出队，同时下一层进队(即根结点的左右子树进队)
当队列为空时，层序遍历完成

在这里插入图片描述

代码展示

//二叉树的层序遍历
void BinaryTreeLevelOrder(BinaryTree* root) 
{
	Queue pq;	//定义队列变量
	//初始化对队列
	InitQueue(&pq);

	//当root不为空时,就进队
	if (root != NULL)
	{
		//结点入队
		QueuePush(&pq,root);
	}
	//队列不为空就继续进行层序遍历
	//队列为空时，层序遍历完成
	
	int levelsize = 1;
	while ( !QueueEmpty(&pq) )
	{
		//一层一层出
		while (levelsize--)
		{
			//队头出队，队尾进队
			//先获取队头结点
			BinaryTree* headnode = QueueFront(&pq);
			//上一层出队
			QueuePop(&pq);
			//打印队头结点的值
			printf("%d- ", headnode->val);

			//下一层进队，即队头结点的左右子树结点入队
			//前提时，左右子树结点不能为空
			if (headnode->left)
			{
				QueuePush(&pq, headnode->left);
			}
			if (headnode->right)
			{
				QueuePush(&pq, headnode->right);
			}
		}
		printf("\n");
		levelsize = QueueSize(&pq);
	}

	//销毁队列
	QueueDestroy(&pq);

}

3. 二叉树的相关操作

(1) 二叉树的初始化

这里使用动态函数来开辟二叉树的结点，给结点赋值同时进行把该节点的左右子树暂时置NULL,最后通过返回该结点的地址(避免使用二级指针了)

代码展示

//二叉树的初始化
BinaryTree* InitTreeNode(int x) 
{
	//动态开辟
	BinaryTree* node = (BinaryTree*)malloc(sizeof(BinaryTree));
	assert(node); //断言避免指针为空
	node->val = x;
	node->left = NULL;
	node->right = NULL;
	return node;	//通过返回函数来进行创建结点
}

在这里插入图片描述

(2) 二叉树的结点的手动创建

有时候方便调试，需要手动创建二叉树
同创建完成后通过返回根节点的地址

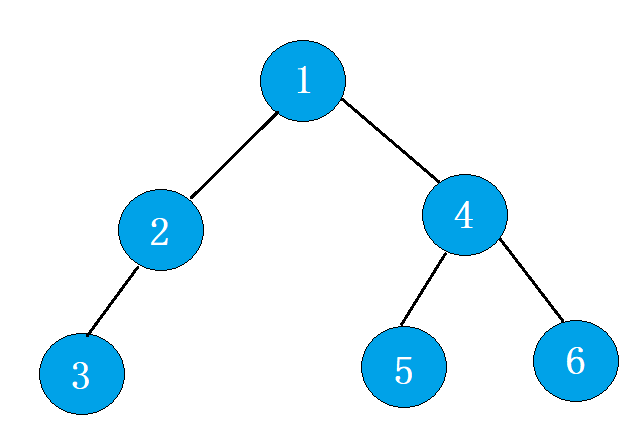
在这里插入图片描述

代码展示

//二叉树的手动构建
BinaryTree* CreateTree() 
{
	BinaryTree* node1 = InitTreeNode(1);
	BinaryTree* node2 = InitTreeNode(2);
	BinaryTree* node3 = InitTreeNode(3);
	BinaryTree* node4 = InitTreeNode(4);
	BinaryTree* node5 = InitTreeNode(5);
	BinaryTree* node6 = InitTreeNode(6);

	node1->left = node2;
	node1->right = node4;
	node2->left = node3;
	node4->left = node5;
	node4->right = node6;

	return node1;	//返回根结点

}

(3) 二叉树结点的个数

即计算有多少结点
先从根结点开始，若根节点为空，就返回0，如果不为空，递归左子树，然后递归右子树。(当然这里递归顺序没有要求，也可以先进行递归右子树然后再递归左子树)

使用分治思想：
树的结点个数 = 左子树结点个数 + 右子树结点个数 + 1 ;

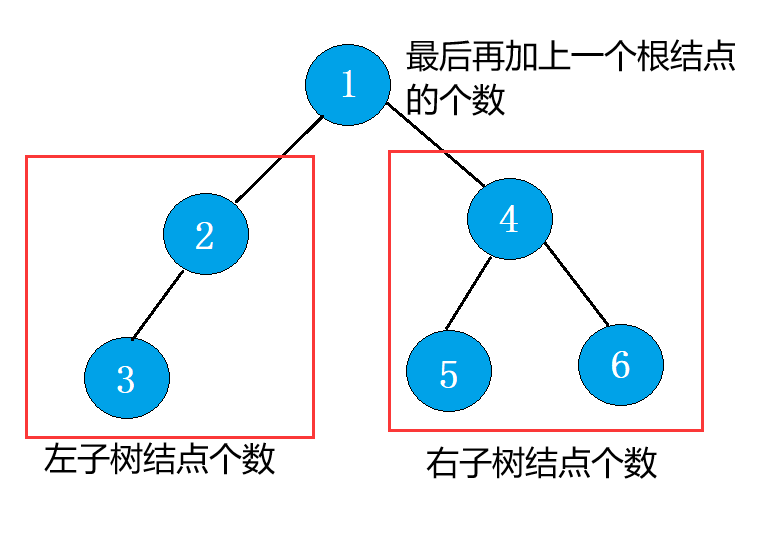
在这里插入图片描述

代码展示

//计算二叉树结点的个数
int BinaryTreeSize(BinaryTree* root) 
{
	//根结点开始
	//访问左子树，访问右子树
	if (root == NULL)
		return 0;

	return BinaryTreeSize(root->left)+BinaryTreeSize(root->right) + 1;
}

优化一下：

int BinaryTreeSize(BinaryTree* root) 
{
	return root == NULL ? 0 : BinaryTreeSize(root->left)+BinaryTreeSize(root->right) + 1;
}

(4) 二叉树叶子结点的个数

叶子结点：结点度为0的结点
使用递归，返回条件为

如果根结点为空返回 0
如果根结点不为空且左右子树都为空说明是叶子返回1
root 不是空,也不是叶子，分治法，叶子数 = 左子树的叶子+右子树的叶子

代码展示

//计算叶子结点的个数
int BinaryTreeLeafSzie(BinaryTree* root) 
{	
	//分治法
	// 叶子结点树 = 左子树叶子 + 右子树叶子
	//结点为空返回0
	if (root == NULL)
		return 0;
	//root不为空，左右子树为空是叶子,返回1
	if (root->left == NULL && root->right == NULL)
		return 1;
	//root不为空且左右子树都不为空,继续递归左右子树
	return BinaryTreeLeafSzie(root->left) + BinaryTreeLeafSzie(root->right);
}

(5) 二叉树的高度

分治法
树高 = 左子树与右子树中较高的树 +1
递归条件

root 为空返回 0
root 不为空计算左右子树中较高的，返回较高的+1

代码展示

//计算二叉树的高度
int BinaryTreeHeight(BinaryTree* root) 
{
	//树高 = 左子树与右子树中较高的树 +1
	if (root == NULL)
		return 0;
	//记录左子树高
	int leftHeight = BinaryTreeHeight(root->left);
	//记录右子树高
	int rightHeight = BinaryTreeHeight(root->right);
	//返回较高树同时+1
	return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}

方法二：

//计算树高方法二
int BinaryTreeHeight(BinaryTree* root)
{
	//树高 = 左子树与右子树中较高的树 +1
	if (root == NULL)
		return 0;
	return fmax(BinaryTreeHeight(root->left),BinaryTreeHeight(root->right))+1;
}

如图：
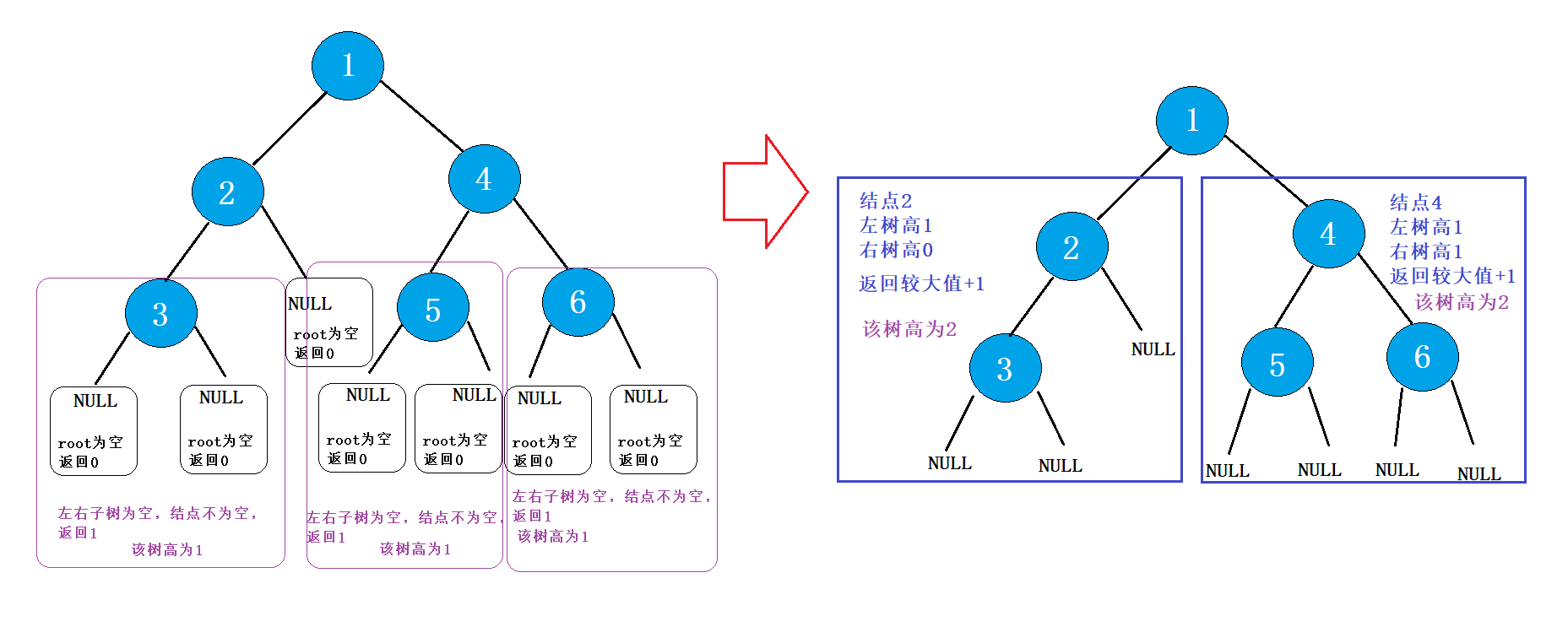
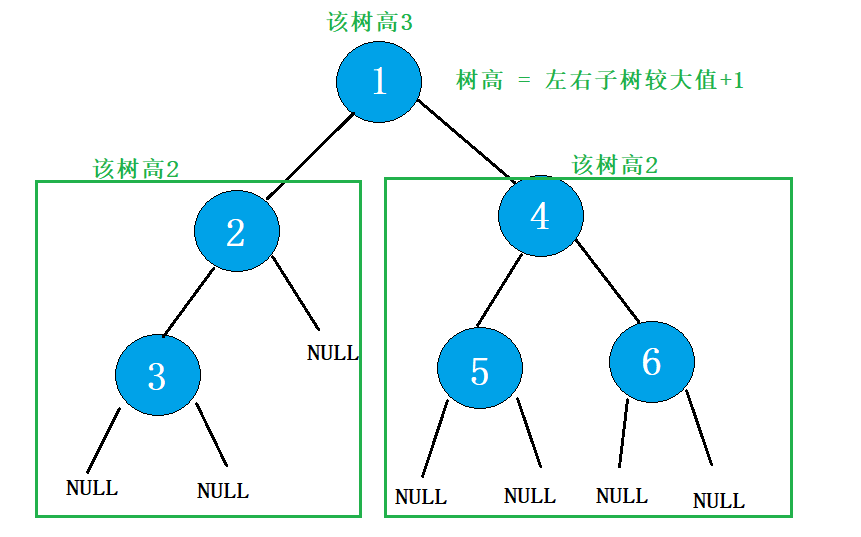
在这里插入图片描述

(6) 第k层结点个数

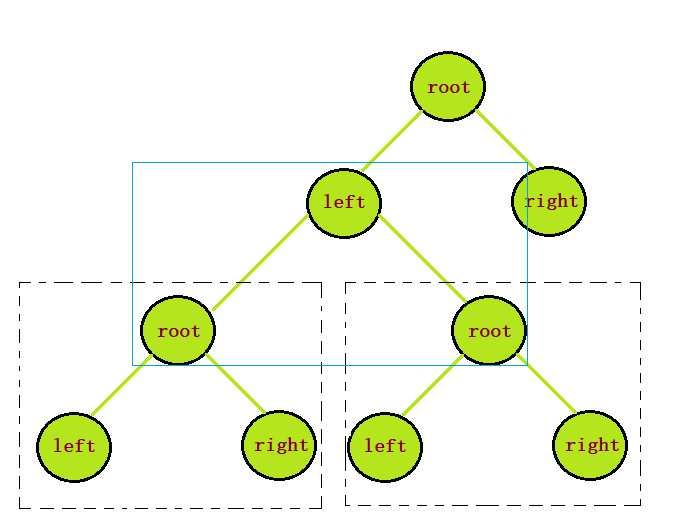
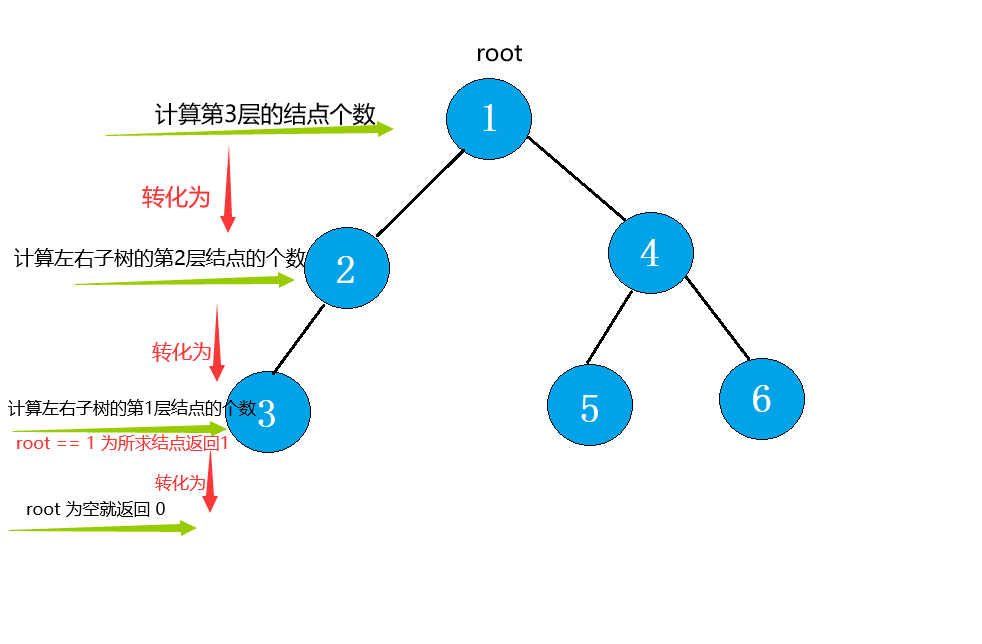
计算第k 层的结点个数，这里我们可以转化为去求左子树的 k - 1 层和右子树的 k - 1 层的结点的个数

递归条件：

root 为空，返回0
root不为空且 k == 1,返回1
root不为空且 k > 1, 返回左子树的 k - 1 层 + 右子树的 k - 1 层

在这里插入图片描述
代码展示

//二叉树第k层结点的个数
int BinaryTreeLevelSizeK(BinaryTree* root, int k) 
{
	assert(k >= 1); //层数最小为1
	//第k层结点个数 = 左子树k-1层 + 右子树k-1层 的结点个数
	if (root == NULL)
		return 0;
	//结点不为空，k == 1,返回1
	if (k == 1)
		return 1;
	//k>1,继续递归左右子树的 k-1 一层
	return BinaryTreeLevelSizeK(root->left,k-1) + BinaryTreeLevelSizeK(root->right,k - 1);
}

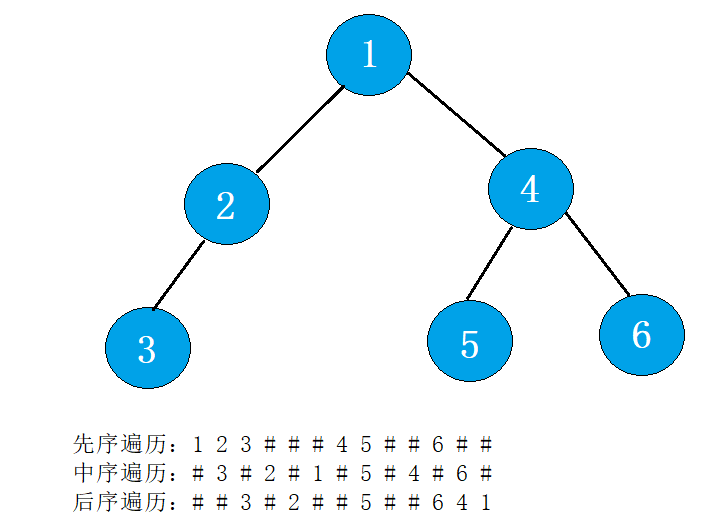
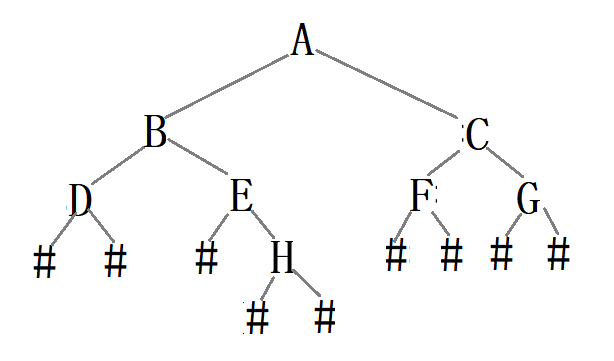
(7) 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树

当元素的值是 ‘#’ 时，表示为空，数组下标加一；不是‘#’时，动态分配内存空间并给结点赋值。然后递归左右子树，最后返回根结点

代码展示

// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BinaryTree* BinaryTreeCreate(BTDataType* arr, int* pi) 
{
	//# 表示为空
	if (arr[*(pi)] == '#')
	{
		(*pi)++;
		return NULL;
	}
	
	//不是＃，就动态分配内存空间
	BinaryTree* root = (BinaryTree*)malloc(sizeof(BinaryTree));
	if (root == NULL)
	{
		perror("malloc fail");
		exit(-1);
	}
	//结点赋值
	root->val = arr[(*pi)++];
	//递归左右子树
	root->left = BinaryTreeCreate(arr,pi);
	root->right = BinaryTreeCreate(arr,pi);
	
	//返回根结点
	return root;
}

如图：
在这里插入图片描述

(8) 二叉树查找值为x的结点

首先当根结点为空直接返回空，当root不为空且结点值等于x的时候直接返回结点，当root不为空且结点值不等于x的时候，递归左右子树(通过记录左右子树的结点来避免重复去找，还需注意左右结点为空的情况)

代码展示

//二叉树查找值为x的结点
BinaryTree* BinaryTreeFind(BinaryTree* root, BTDataType x)
{
	//结点为空直接返回空
	if (root == NULL)
		return NULL;
	//root不为空，结点值 = x ,就返回结点
	if (root->val == x) 
	{
		return root;
	}
	//root不为空，结点值 != x ，递归左右子树
	//但是递归左右子树时，注意子树为空的情况
	//记录结点，避免重复去找
	BinaryTree* left = BinaryTreeFind(root->left, x);
	if (left)
		return left;
	BinaryTree* right = BinaryTreeFind(root->right, x);
	if (right)
		return right;

	//左右结点都为空，返回空
	return NULL;
}

在这里插入图片描述

(9) 判断是否为完全二叉树

除了最后一层外，也就是前n-1层的结点都必须是满的，最后一层的结点从左到右连续存在，不能有间隔

完全二叉树
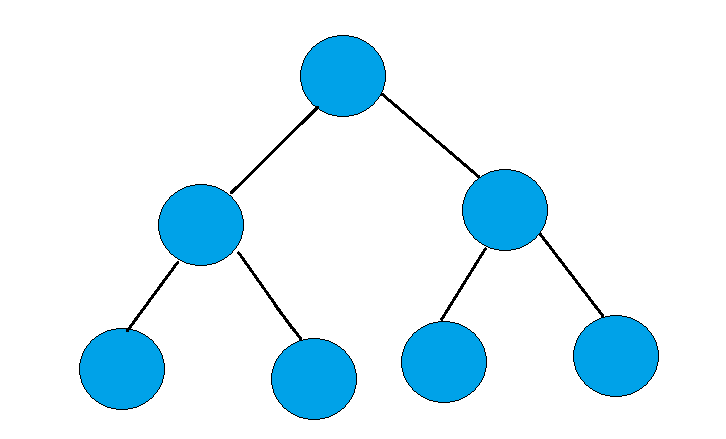
在这里插入图片描述

不是完全二叉树，情况一：
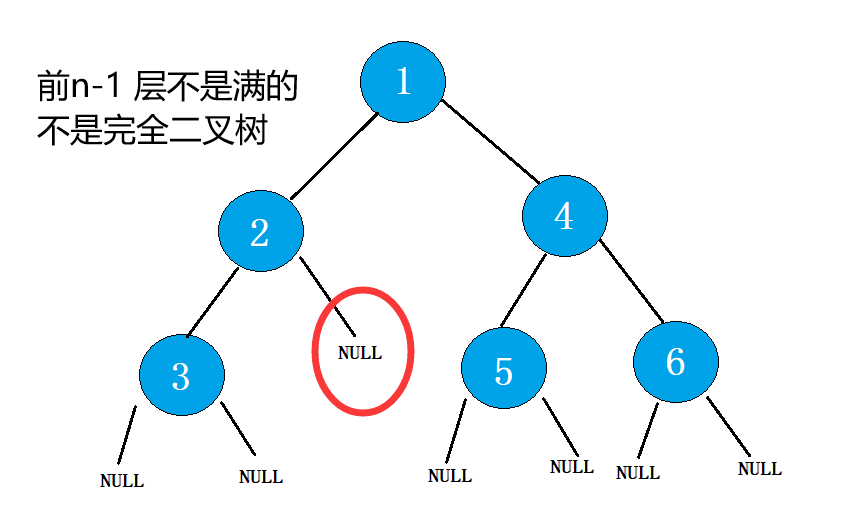
在这里插入图片描述
情况二 :

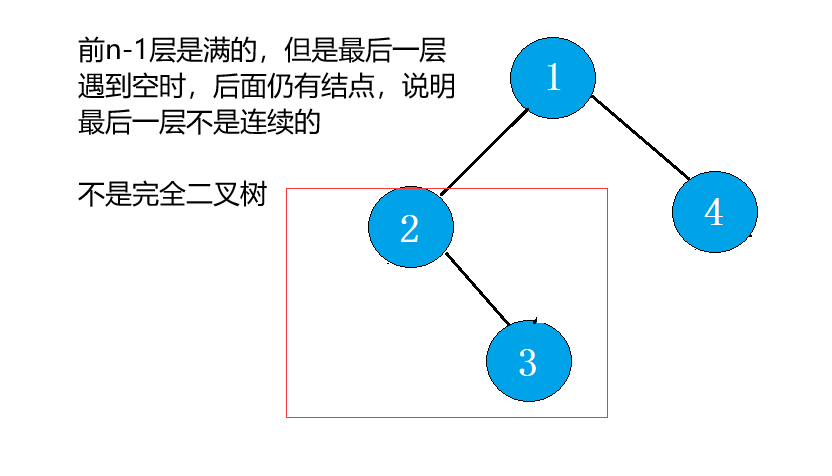
在这里插入图片描述

判断是否为完全二叉树，我们需要进行借助层序遍历,层序遍历时当遇到结点为空时，跳出循环。然后在借助一次层序遍历，如果遇到了不为空的结点，即不是完全二叉树。否则是完全二叉树。

代码展示

//判断是否为完全二叉树
bool BinaryTreeComplete(BinaryTree* root)
{
	//借助层序遍历
	//遇到空时，再层序遍历后面都为空，就是完全二叉树
	//否则不是
	Queue pq;
	QueueInit(&pq);
	//结点不为空就进队列
	if (root)
	{
		QueuePush(&pq, root);
	}
	while (!QueueEmpty(&pq))
	{
		//先取队头
		BinaryTree* headnode = QueueFront(&pq);
		//上一层出队
		QueuePop(&pq);
		//只要遇到空就停止层序遍历
		if (headnode == NULL)
		{
			break;	//跳出循环
		}
		//下一层进队
		QueuePush(&pq,headnode->left);
		QueuePush(&pq,headnode->right);
	}

	//再一次层序遍历，只要遇到结点不为空就不是完全二叉树，否则是完全二叉树
	while (!QueueEmpty(&pq)) 
	{
		//先取队头
		BinaryTree* headnode = QueueFront(&pq);
		//上一层出队
		QueuePop(&pq);
		if (headnode)	//结点不为空，此树不是完全二叉树
			return false;	
	}
	
	return true;
}

上述中使用了两次层序遍历

下方的另种方法只使用了一次层序遍历的方法，通过记录值进行确定,当遇到空的时候，记录值为true,当在层序遍历中，发现记录值为true 且结点不为空，说明不是完全二叉树

//判断是否为完全二叉树 法二
bool BinaryTreeComplete(BinaryTree* root) 
{
	//使用一次层序遍历，遍历时，对空进行记录
	Queue pq;
	QueueInit(&pq);
	

	//如果根结点不为空，结点入队
	if (root)
	{
		//注意进队的是结点，不是结点的值
		QueuePush(&pq, root);
	}

	//使用bool类型进行记录
	bool hasEmpty = false;

	while (!QueueEmpty(&pq))
	{
		//获取队头元素
		QDataType headnode = QueueFront(&pq);
		//出队
		QueuePop(&pq);
		if (headnode == NULL) 
		{
			//当队头元素为空时，记录值为true
			hasEmpty = true;
		}
		else
		{
			//当队头结点不为空时，记录值为true，说明前面已经遇到空且后面的结点有不为空的(即不是完全二叉树)
			if (hasEmpty == true)
			{
				//不是完全二叉树
				return false;
			}

			//记录值为false时，没有遇到空
			//继续层序遍历
			//前一层出队，后一层入队
			QueuePush(&pq,headnode->left);
			QueuePush(&pq,headnode->right);
		}
	}
	return true;
}

(10) 二叉树的销毁

把二叉树的所有不为空结点进行一一释放

代码展示

//二叉树的销毁
void BinaryTreeDestroy(BinaryTree* root) 
{
	//需要把二叉树的所有不为空结点进行一一释放
	//root 为空 直接返回
	if (root == NULL)
		return;
	//root不为空，递归左右子树
	BinaryTreeDestroy(root->left);
	BinaryTreeDestroy(root->right);
	free(root);
}