通过层进行高效学习：探索深度神经网络中的层次稀疏表示

news2024/11/25 2:45:52

一、介绍

深度学习中的层次稀疏表示是人工智能领域日益重要的研究领域。本文将探讨分层稀疏表示的概念、它们在深度学习中的意义、应用、挑战和未来方向。

最大限度地提高人工智能的效率和性能：深度学习系统中分层稀疏表示的力量。

二、理解层次稀疏表示

分层稀疏表示是一种在深度学习模型中构建和处理数据的方法。本质上，这些表示涉及以大多数元素为零或接近零（稀疏）的方式对数据进行编码，并以多个级别或层次结构组织。这种方法与密集表示形成对比，密集表示中数据由许多非零元素表示。

分层方面是指数据和特征如何在多个层中构建，每个层的抽象级别不断增加。在深度学习中，这通常对应于神经网络的层，其中较低层捕获基本模式，较高层捕获更复杂、抽象的表示。

三、深度学习的意义

深度学习中层次稀疏表示的重要性在于其效率和有效性。稀疏表示可以显着减少计算负载和内存需求，因为与密集表示相比，涉及的连接和计算更少。这在处理高维数据（例如图像或文本）时特别有价值，因为在这些数据中，密集表示可能会变得大得不切实际。

此外，稀疏表示可以产生更稳健和更通用的模型。通过关注最显着的特征并减少不太重要的数据的影响，这些模型可以更好地识别潜在的模式和关系，从而有可能提高分类、回归或预测等任务的性能。

四、应用领域

分层稀疏表示在各个领域都有应用：

图像处理和计算机视觉：用于对象检测、图像分类和分割等任务，有助于高效处理大型图像数据。
自然语言处理 (NLP)：应用于语言模型和文本分类，能够高效处理大型词汇和文本序列。
生物信息学：用于基因序列分析和蛋白质结构预测，其中高维数据很常见。
推荐系统：用于管理和解释通常在用户-项目交互矩阵中发现的稀疏数据。

五、挑战

尽管有其优点，分层稀疏表示也带来了挑战：

模型复杂性：使用这些表示设计和训练模型可能很复杂，需要仔细考虑稀疏结构和层次结构级别。
数据稀疏性：过度稀疏性可能会导致信息丢失，尤其是在稀疏表示无法有效捕捉数据本质特征的情况下。
优化困难：密集网络中使用的传统优化方法可能无法直接适用于稀疏网络或效率不高。

六、未来发展方向

深度学习中分层稀疏表示的未来似乎很有希望，有几个潜在的方向：

改进的算法：开发专门针对稀疏表示的新算法和训练技术。
硬件优化：设计能够有效处理稀疏计算的硬件，以进一步提高性能增益。
跨域应用：探索量子计算或边缘计算等新兴领域的应用，这些领域的效率至关重要。
与其他 AI 技术集成：将稀疏表示与强化学习或无监督学习等其他 AI 技术相结合，以获得更强大的模型。

代码

创建完整的 Python 代码示例来演示深度学习中的分层稀疏表示涉及几个步骤。我们将首先生成一个合成数据集，然后构建一个包含分层稀疏表示的简单神经网络，最后用绘图可视化结果。

import numpy as np
import matplotlib.pyplot as plt
from tensorflow.keras.layers import Input, Dense
from tensorflow.keras.models import Model
from tensorflow.keras.regularizers import l1
from sklearn.datasets import make_classification

X, y = make_classification(n_samples=1000, n_features=20, n_informative=2, n_redundant=0, n_classes=2, random_state=42)

input_layer = Input(shape=(20,))
sparse_layer = Dense(64, activation='relu', activity_regularizer=l1(0.01))(input_layer)
output_layer = Dense(1, activation='sigmoid')(sparse_layer)

model = Model(inputs=input_layer, outputs=output_layer)
model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['accuracy'])

history = model.fit(X, y, epochs=100, batch_size=32, verbose=0)

plt.plot(history.history['loss'])
plt.title('Model Loss')
plt.ylabel('Loss')
plt.xlabel('Epoch')
plt.legend(['Train'], loc='upper left')
plt.show()

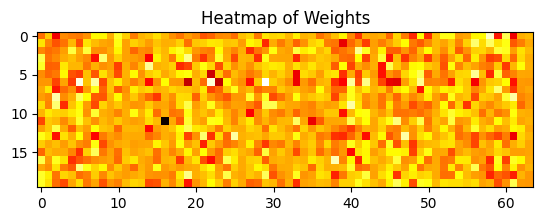
weights = model.layers[1].get_weights()[0] # Get weights of the sparse layer
plt.imshow(weights, cmap='hot', interpolation='nearest')
plt.title('Heatmap of Weights')
plt.show()

non_zero_weights = np.count_nonzero(weights)
total_weights = weights.size
sparsity_percentage = (1 - non_zero_weights / total_weights) * 100
print(f"Sparsity in weights: {sparsity_percentage:.2f}%")