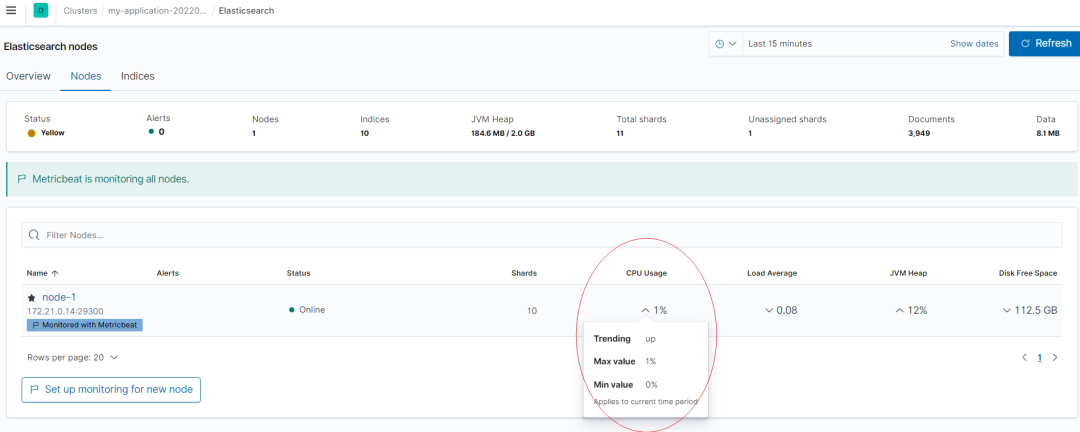
在前两节中,我们推导了生日问题的求解算法,但在数学上的最终目标就是希望能针对问题推导出一个简洁漂亮的公式,就像爱因斯坦著名的质能方程 E = MC^2 那样,毕竟数学是以符号逻辑来看待世界本质的语言,所以絮絮叨叨不是数学,一个掷地有声的符号公式才是数学的范儿。
这里我们需要一些微积分的内容。首先在前面章节中我们推导出 n 个人没有两个人拥有相同生日的概率是:
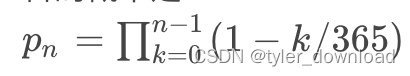
在数学上看到多个数相乘时,第一个处理方法就是把乘法变成加法,因为加法比乘法要容易处理得多。由此我们只要吧上面公式两边同时取 log,那么就能将乘法变成加法:
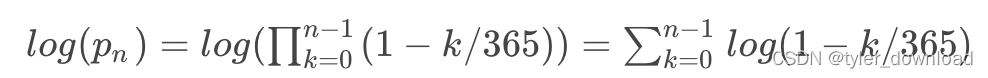
下面我们需要使用微积分的一些技巧,针对 log(1-x)这个公式做一些变换。根据微积分的原理,一个函数在给定点处求导,本质上是函数对应曲线在该点处的切线:

对于函数 f(x),它在点 a 处的切线斜率就是它在 a 点处的导数 f’(a),于是上图中虚线对应的直线方程g(x)就是g(x) = f(a) + f’(a)(x-a)。我们看上面图形可以观察到,黑色虚线与蓝色曲线之间的“缝隙”在蓝色圆点a附近会变小, 也就是当 x 越靠近 a,那么 g(x)与 f(x)的值的差异就越小,当 x=a 时就有 g(a)=f(a),于是当 x 与 a 的距离非常接近时,我们就能用 g(x)的值来近似 f(x)。
对于 f(x)=log(1-x),它的导数为 f’(x)=-1/(1-x),如果我们取 a=0,那么 f’(a)=f’(0)=-1,于是在 0 点处 log(1-x)的切线方程就是 g(x)=f(0)+f’(0)*(x-0)=log(1-0)+(-1)*(x)=0 + (-1)*(x)=-x。回到 log(1-k/365),如果 k 的值距离 365 比较远,那么 k/365 的值就会比较接近 0,于是我们就能用 g(k)来近似 log(1-k/365),也就是:
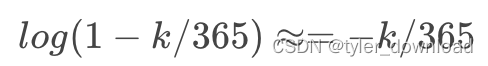
于是就有:

又因为我们有求和公式:
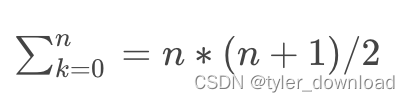
所以有:
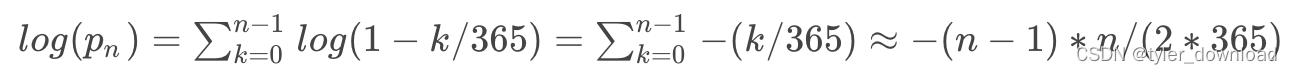
我们把 p(n)=1/2 代入上面公式就有:
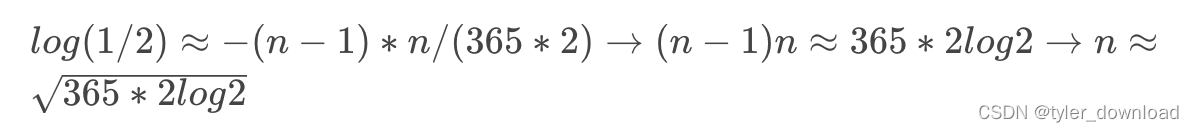
从上面公式可以计算出 n 的值为22.49,由于天数要取整,因此n 的取值就是 23,注意公式中 365 对应的是一年的天数,如果我们不是在地球上而是在火星或者冥王星,那么一年就不是 365 天,我们用变量 D 来表示当地一年的天数,那么对应概率就是:
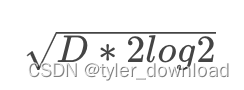
上面公式就是我们要推导的目标,至此数学的逼格才能真正显示出来。更多内容请在 b 站搜索 Coding 迪斯尼。