文章目录
- 盛最多水的容器
- 算法题描述
- 示例
- 示例 1
- 示例 2
- 提示
- 题意拆解
- 解决方案:【双指针】
- 运行结果
- 复杂度分析
- 结束语
盛最多水的容器
盛最多水的容器
算法题描述
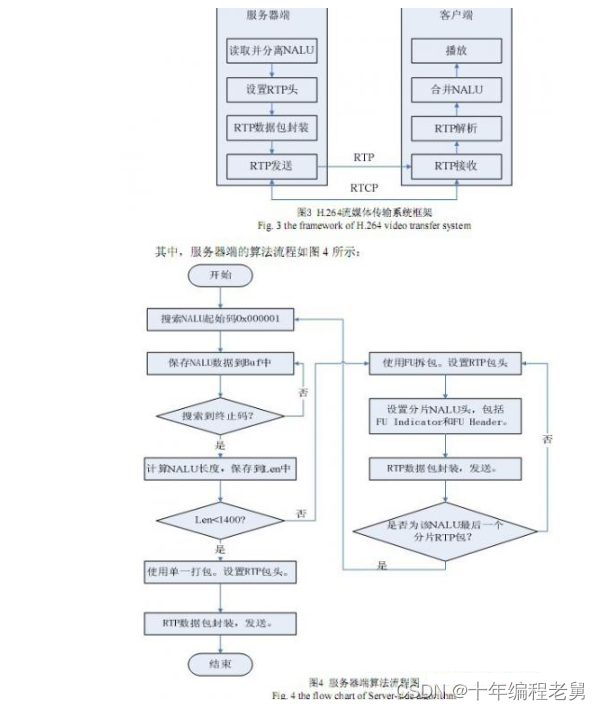
给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
核心任务:返回容器可以储存的【最大水量】。
示例
示例 1
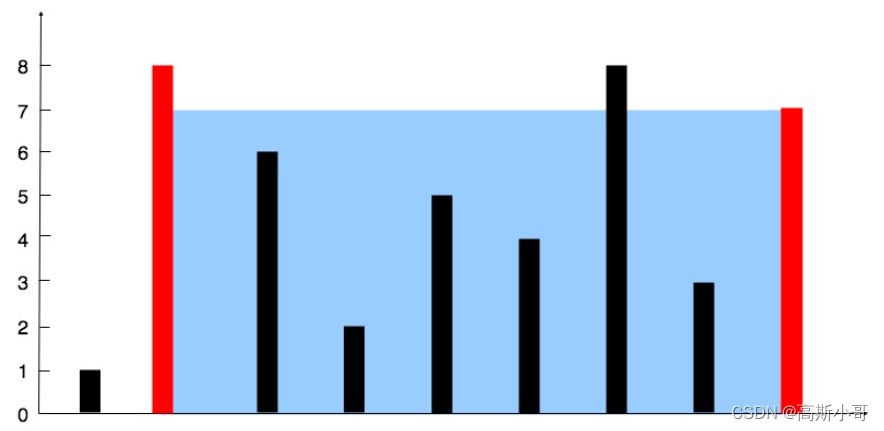
图片来源
-
输入:[1,8,6,2,5,4,8,3,7]
-
输出:49
-
解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
示例 2
-
输入:height = [1,1]
-
输出:1
提示
- n == height.length
- 2 <= n <= 105
- 0 <= height[i] <= 104
题意拆解
【盛最多水的容器】本质上是区间问题,因为我们需要找到两个垂线,它们与x轴构成的区间能够容纳最多的水。这涉及到【比较不同区间的容量】,并【找出最大值】。
问题1:给定区间,即给定左边界left和右边界right,如何确定这个区间能够容纳多少水?
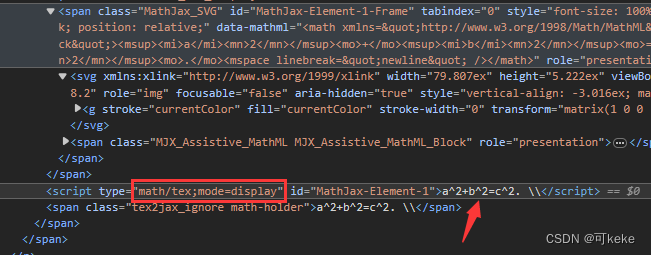
依据木桶原理!!!木桶原理告诉我们,一个木桶盛水的多少,由最短的木板决定。因此,不难确定,当前这个给定区间所能容纳水的面积公式为:
C
u
r
A
r
e
a
=
(
r
i
g
h
t
−
l
e
f
t
)
∗
min
(
h
e
i
g
h
t
[
l
e
f
t
]
,
h
e
i
g
h
t
[
r
i
g
h
t
]
)
Cur Area = (right - left) * \min(height[left], height[right])
CurArea=(right−left)∗min(height[left],height[right])
其中, height[left]表示左边界垂线的高度,height[right]表示右边界垂线的高度。(right - left)表示的是区域的宽度。
问题二:现在已知给定区间的容纳面积,如何才能获取其他区间的容纳面积?
如果我们需要获取其他区间的容纳面积,不可避免地需要移动左指针/右指针以改变左边界/右边界 ===> 自然引出双指针法。
问题三:既然需要移动左/右指针,怎么移动才比较高效?总不能暴力遍历所有区域,每个区域都进行面积的计算和比较吧?
明确本题的核心任务:找到能够容纳最多的水的区域,并返回其容纳面积 ==> 我们可以围绕这个目标设计算法,提前规避一些不必要的比较操作。
根据容纳面积的计算公式,如果我们希望下一个遍历的区域能够比当前的区域的容纳面积大,无非在两个方向上使劲:
-
下一个区域的宽度
(right - left)比当前更宽。这个是不现实的,因为我们的左右边界起始就是数组height的两端。当移动左/右边界时,只可能使宽度变窄,不可能变得更宽。问题四:既然左右指针一开始放在数组两端只会使宽度变得更窄,为什么还要这样设计?不能一开始同时初始化为0吗?
因为会给这个问题增加不确定性,导致无法确定下一步应该移动左边界还是右边界才能使得面积朝着可能变大的方向前进。面积的计算公式是由高度和宽度同时决定的,在遍历的过程中,如果两者的变化都是不确定的,那么最后可能会退化成暴力搜索。
如果我们将左右边界一开始就初始化为数组的左右两端,就可以专注于设计算法去控制高度的变化,因为宽度一定会变窄,只有高度更高才可能出现面积变得更大的情况。
-
下一个区域的高度
(right - left)比当前更高。根据【木桶原理】,一个木桶盛水的多少,由最短的木板决定。因此我们移动当前更高的边界是没有任何意义的(如示例1所示,左边界更高),因为即使左边界在下一步中变得更高,依然逃不过被右边界拖后腿的命运。同时,宽度一定会变窄 ==> 移动高的边界,面积不可能会增加。综上所述,我们只能移动低的边界,如果低的边界变得更高,且高的幅度大于宽变窄的幅度,那么我们便找到了拥有更大容纳面积的区域。
解决方案:【双指针】
代码如下:
class Solution:
def maxArea(self, height: List[int]) -> int:
"""
计算由给定高度列表构成的矩形容器的最大面积。
参数:
height: 一个整数列表,表示每条线的高度。
返回:
返回最大面积。
"""
n = len(height) # 获取高度列表的长度
left = 0 # 左指针
right = n - 1 # 右指针
max_area = 0 # 最大面积初始化为0
while left < right: # 当左指针小于右指针时,继续循环
cur_area = (right - left) * min(height[left], height[right]) # 计算当前矩形的面积
if cur_area > max_area: # 如果当前面积大于最大面积,则更新最大面积
max_area = cur_area
# 根据当前矩形的左边界和右边界的高度(即左右指针所形成的线的高度)决定移动哪个指针
if height[left] < height[right]: # 如果左指针所形成的线的高度较低
left += 1 # 移动左指针
else: # 否则
right -= 1 # 移动右指针
return max_area # 返回最大面积
运行结果
复杂度分析
-
时间复杂度:O(N),其中 N 是数组
height元素的数量。- 双指针遍历
height数组 ==> O(N)
- 双指针遍历
-
空间复杂度:O(1)
- 只需要额外的常数级别的空间 ===> O(1)
结束语
- 亲爱的读者,感谢您花时间阅读我们的博客。我们非常重视您的反馈和意见,因此在这里鼓励您对我们的博客进行评论。
- 您的建议和看法对我们来说非常重要,这有助于我们更好地了解您的需求,并提供更高质量的内容和服务。
- 无论您是喜欢我们的博客还是对其有任何疑问或建议,我们都非常期待您的留言。让我们一起互动,共同进步!谢谢您的支持和参与!
- 我会坚持不懈地创作,并持续优化博文质量,为您提供更好的阅读体验。
- 谢谢您的阅读!