目录
概念:
堆的实现
构建
初始化
销毁
插入元素
往上调整
删除堆顶元素
往下调整
返回堆顶元素
返回有效个数
是否为空
堆排序
Top-k问题
编辑 创建数据
堆top-k
概念:
堆是将数据按照完全二叉树存储方式存储到一维数组中;
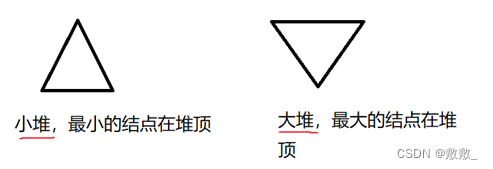
堆分为大堆和小堆:
大堆:父结点大于等于孩子结点;
小堆:父结点小于等于孩子结点;
父结点与(左右)孩子结点关系:
1.父结点 = (孩子结点-1)/2;
2.左结点= (父结点*2)+1;
右结点= (父结点*2)+2;
堆的实现
堆的逻辑结构是完全二叉树,物理结构是一维数组存储;
而独特的结点关系,堆排序也是一种选择排序,
构建
typedef int HPDataType;
typedef struct Heap
{
HPDataType* parr;
int size; //存储的有效数据个数
int capacity; //容量
}Heap;
// 用数组存储 初始化
//堆的初始化
void HeapInit(Heap* php)
{
assert(php);
php->parr = NULL;
php->size = 0;
php->capacity = 0;
}销毁
//堆的销毁
void HeapDestroy(Heap* php)
{
assert(php);
free(php->parr);
php->parr = NULL;
php->size = php->capacity = 0;
free(php);
php = NULL;
}插入元素
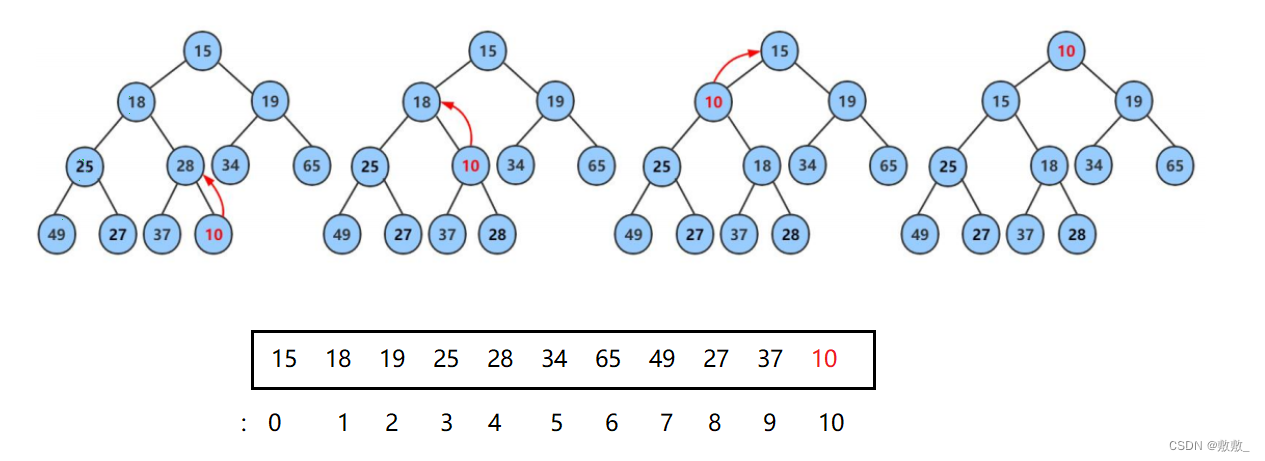
因为堆分为两类,在数据插入时,需要选择适应的调整;
以小堆来说:当插入一个新元素时,插入到堆尾,与父结点比较,相应的往上调整
//堆的插入元素
void HeapPush(Heap* php, HPDataType x)
{
assert(php);
//检查容量
if (php->size == php->capacity)
{
int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;
HPDataType* newparr = (HPDataType*)realloc(php->parr, sizeof(HPDataType) * newcapacity);
if (newparr == NULL)
{
perror("realloc fail");
exit(-1);
}
php->capacity = newcapacity;
php->parr = newparr;
}
php->parr[php->size] = x;
php->size++;
//小堆
//向上调整
AdjustUp(php->parr, php->size - 1);
}往上调整
当插入一个新元素,按照孩子和父结点之间的关系进行比较,交换两结点数据,直到满足堆的性质
//向上调整
void AdjustUp(HPDataType* parr,int size)
{
int child = size;
int parent = (child - 1) / 2;
//小堆=> 父结点<=孩子结点
while (child>0)
{
if (parr[child] < parr[parent])
{
//交换数据
Swap(&parr[child], &parr[parent]);
child = parent; //更新结点位置
parent = (child - 1) / 2;
}
else
{
break;
}
}
}删除堆顶元素
1.将堆顶元素和尾部元素互换位置;
2.将此刻不符合规定的堆顶元素往下调整至相应位置;

// 删除堆顶(根节点)
void HeapPop(Heap* php)
{
assert(php);
//1.堆顶元素和尾部元素置换位置
Swap(&php->parr[0], &php->parr[php->size - 1]);
php->size--; //删掉交换后的堆顶元素
//2.将新站顶元素找到相应位置
//向下调整
AdjustDown(php->parr,php->size,0);
}往下调整
堆顶元素与其孩子结点比较,如何找到较大(较小)的孩子?
可以假设法:假设较大(较小)的孩子为左孩子,然后验证假设;

//向下调整
void AdjustDown(HPDataType* parr,int size,int parent)
{
int child = (parent * 2) + 1;
while (child<size) //
{
//假设左孩子为较小值
if (child+1<size && parr[child + 1] < parr[child]) //验证假设
{
++child; //说明右孩子更小,更换孩子位置
}
//检查是否不符合堆排序结构
if (parr[parent] > parr[child])
{
Swap(&parr[parent], &parr[child]);
//往下更新父结点 孩子结点位置
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}返回堆顶元素
起始值为0;
//返回堆顶元素
HPDataType HeapTop(Heap* php)
{
assert(php);
assert(php->size > 0);
return php->parr[0];
}返回有效个数
注意,构建堆的时候,size是最后一个元素的下一个;
//返回堆内有效数据个数
size_t HeapSize(Heap* php)
{
assert(php);
return php->size; //数组下标0开始
}是否为空
//判断堆是否为空
bool HeapEmpty(Heap* php)
{
return php->size == 0;
}堆排序
以上是一些堆的简单功能实现;算不上真正的堆排序;
假设给定一串数字,4,6,2,1,5,8,2,9;如何将其排序?比如升序;
- 建立一个大堆;
- 将堆顶元素与堆尾元素互换,且将遍历堆的范围-1,保证其想要的值保持不动;
- 将此刻不符合规定的堆顶往下调整,找到次大的值;重复步骤2;
其实相当于第一个元素默认是堆,后面的进行遍历调整;
//排序,升序
void HeapSort(int* parr, int n)
{
//1.建立大堆
for (int i = 1;i < n; i++)
{
justUp(parr, i);
}
//2.堆顶元素与堆尾元素互换,然后将堆size-1(指只需要遍历到的位置)
int end = n - 1;
while (end>0)
{
//堆顶和堆尾 元素呼唤
Swap(&parr[0], &parr[end]);
//往下调整
justDown(parr,end,0);
end--;
}
}也有其他思路;
我们从下面子树往上遍历,而内部调整时往下调整
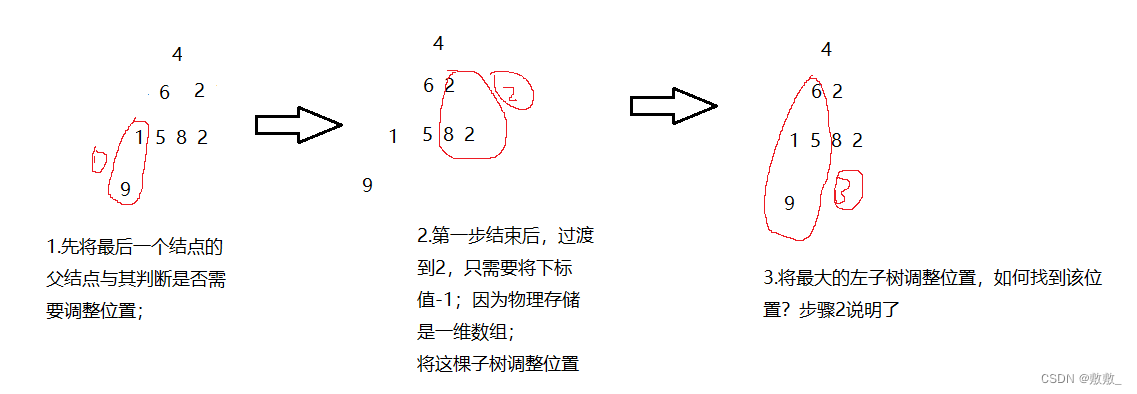
n-1是最后结点下标值,(结点-1)/2 可以得到该结点的父结点,从父结点往下调整;
for (int i = (n-1-1)/2; i >= 0; --i)
{
AdjustDown(parr, n, i);
}
Top-k问题
在排序的基础上,如果这个数很大呢,比如一百万个数,要找到前k个较大值;
此刻建堆排序显然不合适;
1.读取前K个值,建立其小堆;
2.依次读取后面的值,与堆顶比较:如果比堆顶大,替换堆顶进堆,再往下调整;
 创建数据
创建数据
//tok-k 问题
//创建一千万的数据
void CreateNode()
{
// 造数据
int n = 10000000;
srand(time(0));
const char* file = "data.txt";
FILE* fin = fopen(file, "w");
if (fin == NULL)
{
perror("fopen error");
return;
}
for (int i = 0; i < n; ++i)
{
int x = (rand() + i) % 10000000; //+i是 因为随机数产生只有三万个,加上i可以大大减少重复值
fprintf(fin, "%d\n", x);
}
fclose(fin);
}堆top-k
开辟K个数的空间(动态数组);
建立K个数的小堆;
读取文件中值,遍历与堆顶比较,
void HeapTok(const char* file,int k)
{
FILE* fout = fopen(file, "r");
if (fout == NULL)
{
perror("fopen error");
return;
}
//开辟K个数的空间
int* minheap = (int*)malloc(sizeof(int) * k);
if (minheap == NULL)
{
perror("malloc error");
return;
}
//建立K个数的小堆
for (int i = 0; i < k; i++)
{
//从文件流中 读取数据存到 开辟的空间中
fscanf(fout,"%d", &minheap[i]);
//往上调整
AdjustUp(minheap, i);
}
//遍历文件数据
int x = 0;
while (fscanf(fout, "%d", &x) != EOF)
{
if (x > minheap[0])
{
minheap[0] = x;
//往下调
AdjustDown(minheap, k, 0);
}
}
//打印tok
for (int i = 0; i < k; i++)
{
printf("%d ", minheap[i]);
}
free(minheap);
fclose(fout);
}