磁力计LIS2MDL开发.3--九轴姿态解算
- 概述
- 视频教学
- 样品申请
- 完整代码下载
- 使用硬件
- 欧拉角
- 万向节死锁
- 四元数法
- 姿态解算
- 双环PI控制器
- 偏航角
- 陀螺仪解析代码
概述
LIS2MDL 包含三轴磁力计。
lsm6ds3trc包含三轴陀螺仪与三轴加速度计。
姿态有多种数学表示方式,常见的是四元数,欧拉角,矩阵和轴角。他们各自有其自身的优点,在不同的领域使用不同的表示方式。在四轴飞行器中使用到了四元数和欧拉角。
姿态解算选用的旋转顺序为ZYX,即IMU坐标系初始时刻与大地坐标系重合,然后依次绕自己的Z、Y、X轴进行旋转:
绕IMU的Z轴旋转:航向角yaw
绕IMU的Y轴旋转:俯仰角pitch
绕IMU的X轴旋转:横滚角row
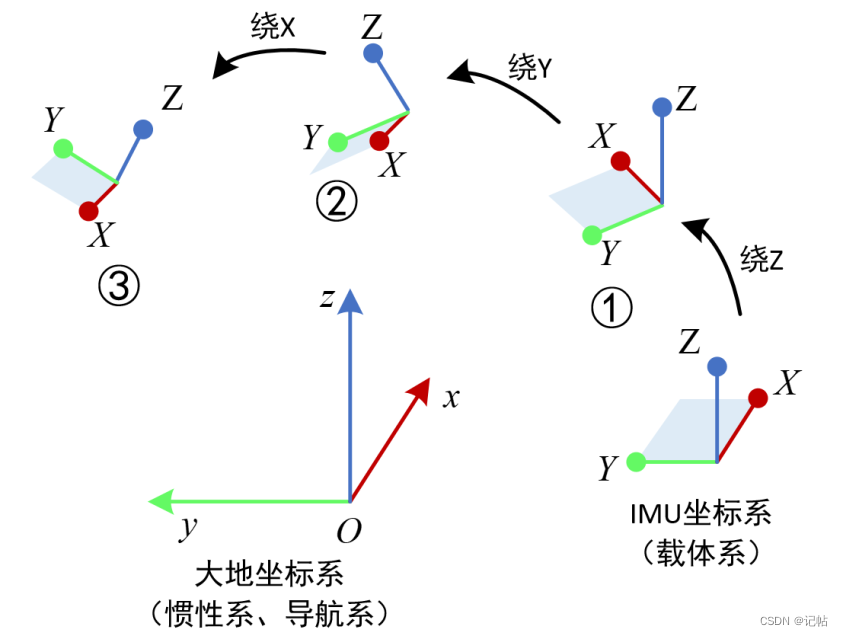
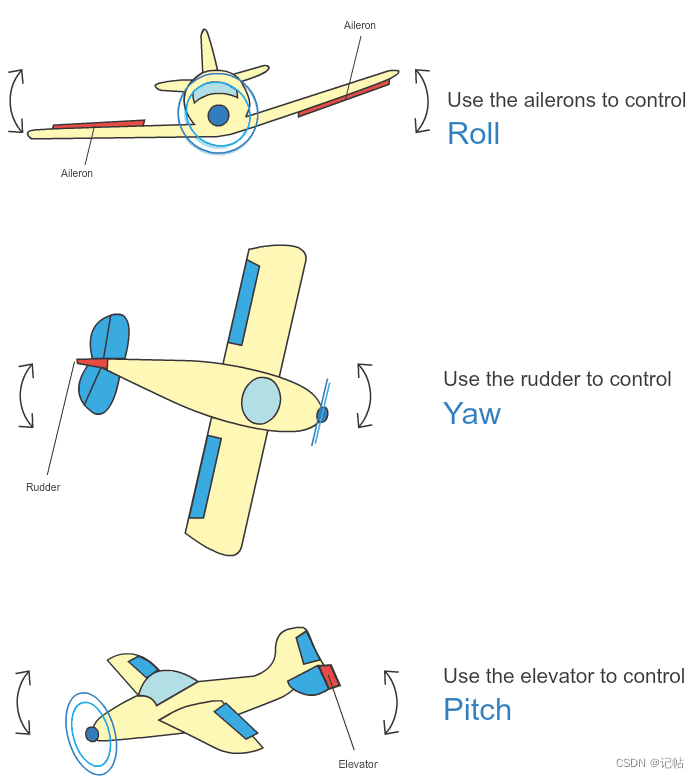
横滚roll,俯仰pitch,偏航yaw的实际含义如下图:
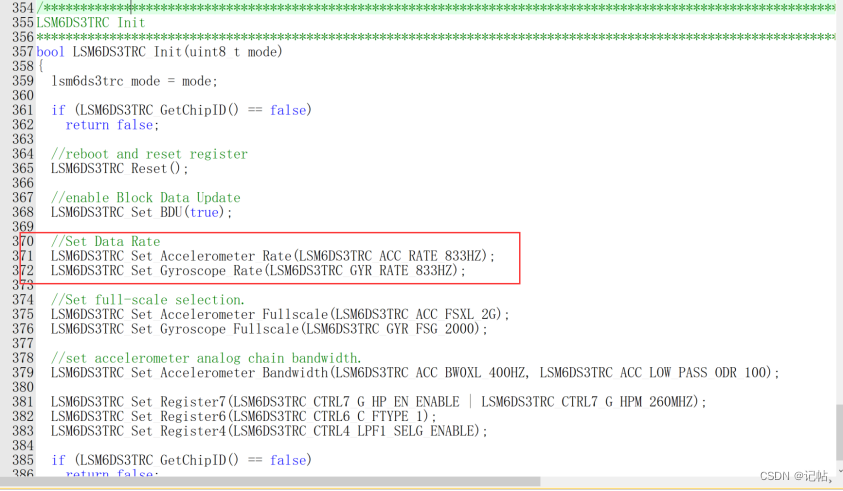
由于需要解析姿态角,故将陀螺仪速度修改快一点。
视频教学
样品申请
https://www.wjx.top/vm/OhcKxJk.aspx#
完整代码下载
使用硬件

欧拉角
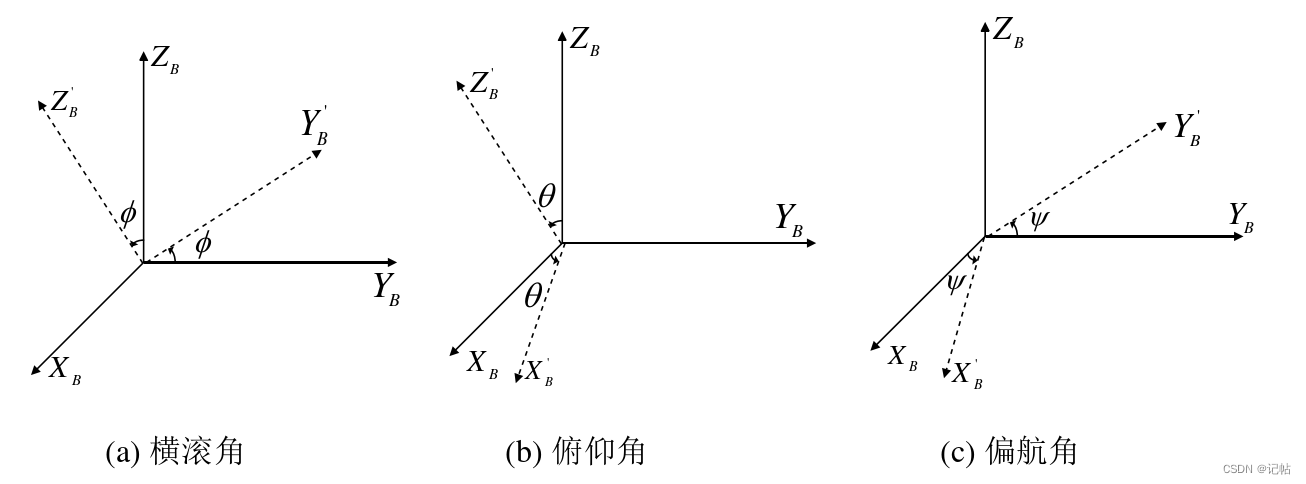
横滚角φ:机体绕OBXB转动,轴Y’B与平面OBXBYB构成的夹角。
俯仰角θ:机体绕OBYB转动,轴Z’B与平面OBYBZB构成的夹角。
偏航角ψ:机体绕OBZB转动,轴X’B与平面OBXBZB构成的夹角。
将姿态角从机体坐标系转换到惯性坐标系中是为了便于分析无人机状态,反映无人机在惯性坐标系下的姿态运动状态,利用齐次线性变换可实现坐标系的转换,旋转矩阵就是在线性变化中产生的,用REB表示惯性坐标系{E}到机体坐标系{B}的变换。
例如,绕OBXB旋转必角,此时两个坐标系存在必的角度差,不再重合。点(x, y, z)的转换方程为:
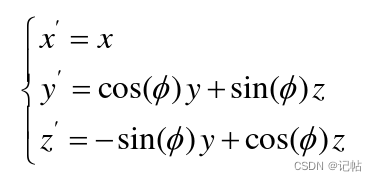
可提取转换矩阵:
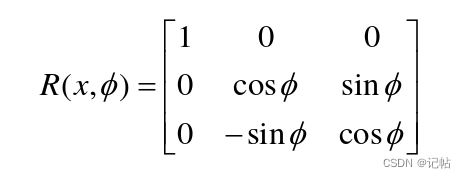
同理,绕口OBYB旋转θ角得:
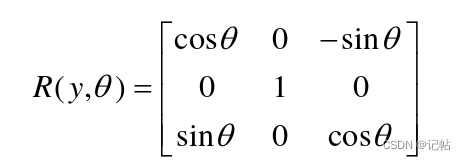
而绕OBZB旋转ψ角得:
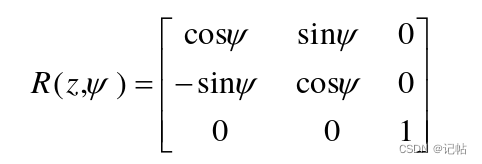
不同旋转顺序有不同的旋转矩阵,按照偏航,俯仰,横滚的顺序,即分别绕X-Y-Z旋转,就可计算出旋转矩阵REB,REB等于依次旋转所得的矩阵连乘,且顺序为从右向左排列。
万向节死锁
当俯仰角θ=±Π/2时,横滚运动与偏航运动的旋转轴重合,出现万向节死锁现象,在空间失去了一个自由度。如式所示,φ或ψ的变化具有相同的效果,因此不再具有唯一性啊。
四元数法
本文选择的是四元数法进行姿态解算。无人机姿态解算方法主要有四种,它们各自的优缺点如下图所示。欧拉角法不能用于计算飞行器的全姿态角,且难以实时计算而不易于工程应用。方向余弦法不会出现“奇点”现象,但计算量大,效率低。四元数法避免了复杂的三角函数运算,变为求解线性微分方程,算法简单易操作,且不存在角度奇异性问题,可以更好的线性化系统,是一种更实用的工程方法。
四元数的概念诞生在1843年的爱尔兰,是数学家哈密顿研究空间几何时提出。在如今的导航技术领域,四元数的优势逐渐被发现,得到了研究者们的广泛关注,并逐渐应用在姿态解算领域。
四元数是由四个元构成的数Q(q0,q1,q2,q3) = q0 + q1i + q2j + q3k;其中,q0,q1,q2,q3是实数,i,j,k既是互相正交的单位向量,又是虚单位根号-1。四元数即可看作四维空间中的一个向量,又可以看做一个超复数。对于后续有一个重要的变化需要记住:
Q=q0 + q1i + q2j + q3k
可视为一个超复数,Q 的共轭复数记为
Q’=q0 - q1i - q2j - q3k
Q°称为Q的共轭四元数。
同时,有
ij=k,jk=i,ki=j,ji=-k,kj=-i,ik=-j
i2 = j2 = k2 =ijk=-1

其中,i、j、k是相互正交的单位向量,其几何意义可理解为分别绕三个坐标轴的旋转,q0、q1、q2、q3为常数,有
通过四元数进行欧拉角求解,可以减少芯片运算负担,提高运算速度。
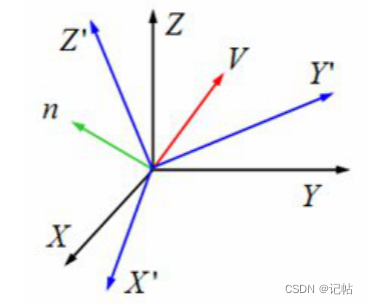
一个矢量V相对于坐标系OXYZ固定:V = xi + yj + zk;坐标系OXYZ转动了Q得到一个新坐标系OX’Y’Z’:V = x’i’ + y’j‘ + z’k’;设四元数Ve、Ve‘
Ve = xi + yj + zk;
Ve’ = x’i + y’j + z’k;
则Ve’ = Q* Ve * Q’;
设Q = q0 + q1i + q2j + q3k;则Q’ = q0 - q1i - q2j - q3k;
则Ve’ = Q* Ve * Q’=(q0 + q1i + q2j + q3k) * (0+xi + yj + zk) + (q0 - q1i - q2j - q3k)
可以算出
x’=(q0 ^2+q1 ^2-q2 ^2-q3 ^2)x+2(q1q2+ q1q3)y+2(q1q3-q0q2)z
y’ = 2(q1q2-q0q3)x+(q0 ^2-q1 ^2+q2 ^2-q3 ^2)y+2(q2q3+q0q1)z
z’ = 2(q1q3+q0q2)x+2(q2q3-q0q1)y+(q0 ^2-q1 ^2-q2 ^2+q3 ^2)z
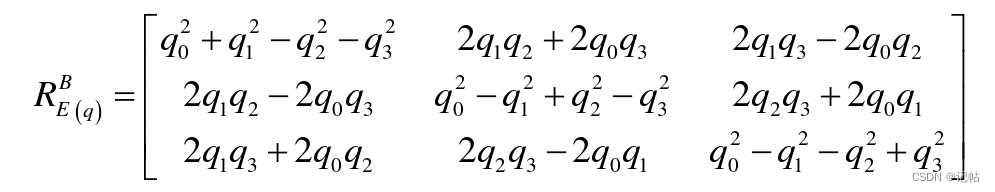
结合
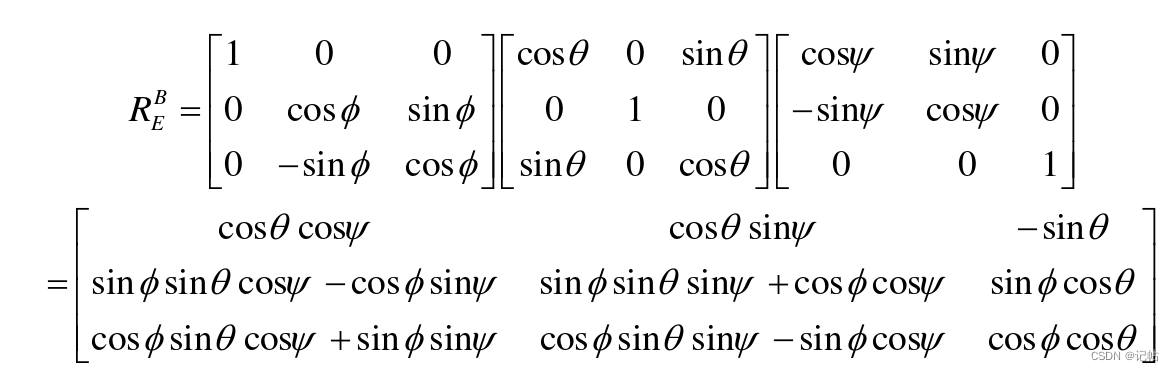
可以反推
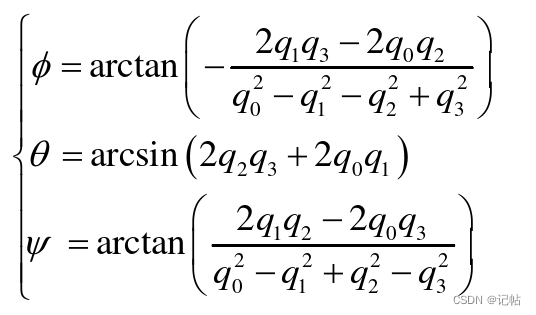
Pitch = asin(2 * q2 * q3 + 2 * q0* q1)* 57.3; // pitch ,转换为度数
Roll = atan2(-2 * q1 * q3 + 2 * q0 * q2, q0*q0-q1*q1-q2*q2+q3*q3)* 57.3; // rollv
Yaw = atan2(2*(q1*q2 - q0*q3),q0*q0-q1*q1+q2*q2-q3*q3) * 57.3; //偏移太大,
将加速度的三维向量转为单位向量
// 测量正常化
norm = sqrt(ax*ax + ay*ay + az*az);
ax = ax / norm; //单位化
ay = ay / norm;
az = az / norm;
世界坐标系重力分向量是通过方向旋转矩阵的最后一列的三个元素乘上加速度就可以算出机体坐标系中的重力向量。
// 估计方向的重力
vx = 2*(q1*q3 - q0*q2);//由下向上方向的加速度在加速度计X分量
vy = 2*(q0*q1 + q2*q3);//由下向上方向的加速度在加速度计X分量
vz = q0*q0 - q1*q1 - q2*q2 + q3*q3;//由下向上方向的加速度在加速度计Z分量
将磁力计的三维向量转为单位向量。
norm = sqrt(mx*mx + my*my + mz*mz);
mx = mx / norm;
my = my / norm;
mz = mz / norm;
计算地磁计在理论地磁坐标系下的机体上三个轴的分量:
● hx, hy, hz 分别表示地磁计测量值在机体坐标系下的x、y、z轴分量。
● 这一步通过方向余弦矩阵(DCM)将地磁计测量值从地磁坐标系转换到机体坐标系。
// 这里计算得到的是地磁计在理论地磁坐标系下的机体上三个轴的分量
hx = 2*mx*(0.5 - q2*q2 - q3*q3) + 2*my*(q1*q2 - q0*q3) + 2*mz*(q1*q3 + q0*q2);
hy = 2*mx*(q1*q2 + q0*q3) + 2*my*(0.5 - q1*q1 - q3*q3) + 2*mz*(q2*q3 - q0*q1);
hz = 2*mx*(q1*q3 - q0*q2) + 2*my*(q2*q3 + q0*q1) + 2*mz*(0.5 - q1*q1 - q2*q2);
计算磁北方向与当前航向角的夹角:
● bx 表示地磁计测量值与磁北方向的夹角,也即当前航向角。
● bx 的计算使用了地磁计在机体坐标系下的x和z轴分量,通过计算角度来表示航向角。
//bx计算的是当前航向角和磁北的夹角,也就是北天东坐标下的航向角
//当罗盘水平旋转的时候,航向角在0-360之间变化
bx = sqrt((hx*hx) + (hy*hy));
bz = hz;
将地磁计在机体坐标系下的磁向量转换到机体坐标系:
● 类似之前的步骤,使用方向余弦矩阵(DCM)将地磁计测量值从机体坐标系转换到地磁坐标系。
● 得到角速度分量 wx, wy, wz,这些值在姿态融合中用于更新四元数。
//地磁计在n系下磁向量转换到b系下,反向使用DCM得到
wx = 2*bx*(0.5 - q2*q2 - q3*q3) + 2*bz*(q1*q3 - q0*q2);
wy = 2*bx*(q1*q2 - q0*q3) + 2*bz*(q0*q1 + q2*q3);
wz = 2*bx*(q0*q2 + q1*q3) + 2*bz*(0.5 - q1*q1 - q2*q2);
这些步骤的目的是将地磁计测量值转换到机体坐标系中,并结合加速度计的测量值估计机体坐标系中的方向和重力向量。这样的处理是为了在姿态融合算法中使用这些数据,以更准确地估计设备的方向。请确保在使用这段代码时,四元数和传感器数据的值都已经被正确更新。
姿态解算
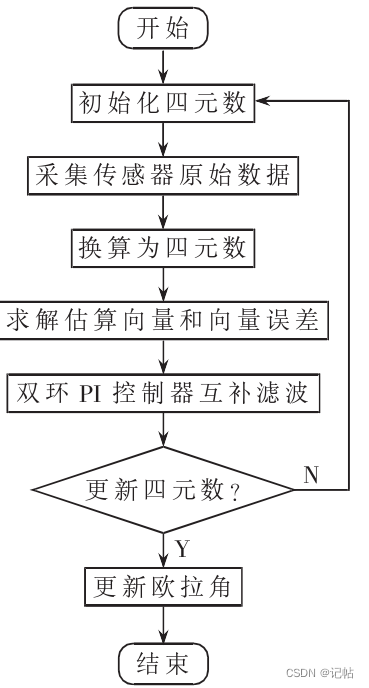
双环PI控制器
陀螺仪能够迅速响应设备的旋转,在短时间内误差较小且可靠。然而,因为温度漂移、零漂移和积分误差会随时间累积,陀螺仪的长时间精度受到影响。在静止状态下,加速度计的漂移很小,其倾角求解过程中不存在积分误差,但在飞行过程中,加速度计受到发动机和机架振动以及转动和运动加速度的干扰。磁罗盘测量的地磁向量在特定地理范围内可视为不变,但磁罗盘易受硬磁场和软磁场干扰。
因此,若系统外环采用九轴姿态传感器(包括三轴加速度计、三轴磁罗盘和三轴陀螺仪)进行数据融合,磁罗盘易受干扰可能导致融合后的数据仍有较大误差。为此,在内环使用六轴姿态传感器(包括三轴加速度计和三轴陀螺仪)进行数据融合,对融合后的传感器姿态偏差进行二次修正,以提高整体精度。
外环九轴姿态传感器数据融合,记在飞行器机体坐标系下an=[ax ay az]T和mn=[mx my mz]T分别为加速度计和磁罗盘实际测量得到的重力向量和地磁向量。
记vn=[vx vy vz]T和wn=[mx my mz]T是将地理坐标系下重力向量kb=[0 0 1g]T和地磁向量nb=[nx 0 nz]T(不考虑地理磁偏角因素,将机头固定向北)通过四元数坐标换算成机体坐标系下的重力向量和地磁向量。向量之间的误差为坐标轴的旋转误差,可以用向量的叉积en=[ex ey ez]T表示,如下所示。
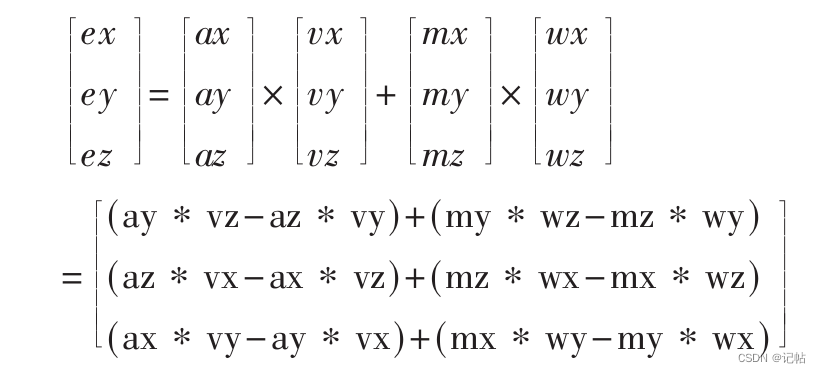
由于我的LSM6DS3TR-C为六轴,不带三轴陀螺仪,故代码如下。
//这个叉积向量仍旧是位于机体坐标系上的,而陀螺积分误差也是在机体坐标系,而且叉积的大小与陀螺积分误差成正比,正好拿来纠正陀螺。
//(你可以自己拿东西想象一下)由于陀螺是对机体直接积分,所以对陀螺的纠正量会直接体现在对机体坐标系的纠正。
ex = (ay*vz - az*vy);
ey = (az*vx - ax*vz);
ez = (ax*vy - ay*vx);
添加磁力计之后代码如下所示。
//这个叉积向量仍旧是位于机体坐标系上的,而陀螺积分误差也是在机体坐标系,而且叉积的大小与陀螺积分误差成正比,正好拿来纠正陀螺。
//(你可以自己拿东西想象一下)由于陀螺是对机体直接积分,所以对陀螺的纠正量会直接体现在对机体坐标系的纠正。
// ex = (ay*vz - az*vy);
// ey = (az*vx - ax*vz);
// ez = (ax*vy - ay*vx);
ex = (ay*vz - az*vy) + (my*wz - mz*wy);
ey = (az*vx - ax*vz) + (mz*wx - mx*wz);
ez = (ax*vy - ay*vx) + (mx*wy - my*wx);
由于陀螺仪是对机体直接积分,所以,陀螺仪的误差可以体现为机体坐标的误差。因此修正坐标轴的误差可以达到修正陀螺仪误差的目的,从而将加速度计和磁罗盘进行修正陀螺仪,实现了九轴的数据融合。即如果陀螺仪按照叉积误差的轴,转动叉积误差的角度,就可以消除机体坐标上实际测量的重力向量和地磁向量和坐标换算后的重力向量和地磁向量之间的误差。
PI调节器的比例部分用于迅速纠正陀螺仪误差,积分部分用于消除稳态偏差。PI调节器的比例系数和积分系数自己去修正。陀螺仪经过外环PI控制器修正姿态误差后输出值为了gn =[gx gy gz]T
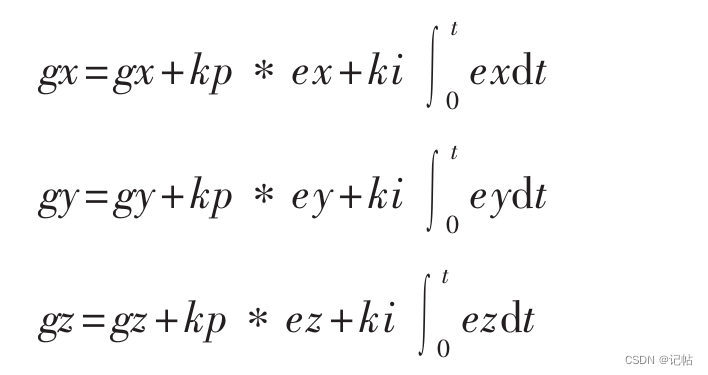
// 积分误差比例积分增益,计算陀螺仪测量的重力向量与估计方向的重力向量之间的误差。
// exInt = exInt + ex*Ki;
// eyInt = eyInt + ey*Ki;
// ezInt = ezInt + ez*Ki;
/* PI */
if(ex != 0.0f && ey != 0.0f && ez != 0.0f)
{
exInt = exInt + ex*Ki*halfT;
eyInt = eyInt + ey*Ki*halfT;
ezInt = ezInt + ez*Ki*halfT;
// 调整后的陀螺仪测量,使用叉积误差来进行比例-积分(PI)修正陀螺仪的零偏。将修正量乘以比例增益Kp,并加上之前计算的积分误差exInt、eyInt和ezInt。
// gx = gx + Kp*ex + exInt;
// gy = gy + Kp*ey + eyInt;
// gz = gz + Kp*ez + ezInt;
gx = gx + Kp*ex + exInt;
gy = gy + Kp*ey + eyInt;
gz = gz + Kp*ez + ezInt;
}
内环的六轴姿态传感器数据融合是将地理坐标系下的重力场向量与加速度计在机体坐标系下采集到的重力向量进行叉乘,求出两者向量误差。并通过PI控制器修正向量误差,从而达到修正外环九轴数据融合后的陀螺仪的偏差的目的。在每个姿态解算周期读取出机体坐标系下双环PI控制后的陀螺仪的角速率
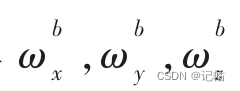
整合四元数率和正常化,根据陀螺仪的测量值和比例-积分修正值,对四元数进行更新。
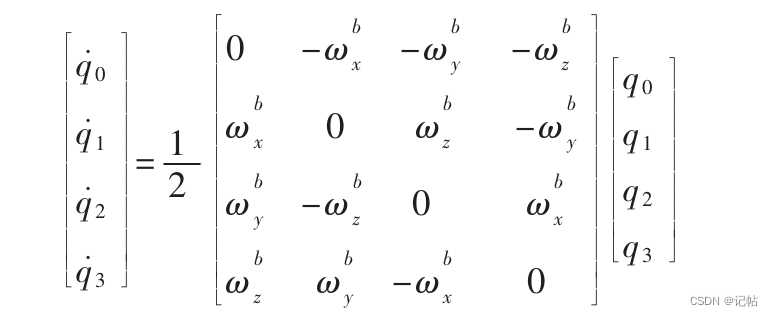
// 整合四元数率和正常化,根据陀螺仪的测量值和比例-积分修正值,对四元数进行更新。根据微分方程的离散化形式,将四元数的每个分量加上相应的微分项乘以采样周期的一半(halfT)。
q0 = q0 + (-q1*gx - q2*gy - q3*gz)*halfT;
q1 = q1 + (q0*gx + q2*gz - q3*gy)*halfT;
q2 = q2 + (q0*gy - q1*gz + q3*gx)*halfT;
q3 = q3 + (q0*gz + q1*gy - q2*gx)*halfT;
// 正常化四元数
norm = sqrt(q0*q0 + q1*q1 + q2*q2 + q3*q3);
q0 = q0 / norm;
q1 = q1 / norm;
q2 = q2 / norm;
q3 = q3 / norm;
偏航角
六轴传感器(包括三轴加速度计和三轴陀螺仪)可以用于估算设备在空间中的姿态,包括俯仰角(Pitch)、横滚角(Roll)和偏航角(Yaw)。然而,六轴传感器仅依赖陀螺仪和加速度计数据,可能无法准确测量偏航角(Yaw),原因如下:
无磁场参考:六轴传感器缺少磁罗盘,没有固定的参考方向。因此,在长时间内,陀螺仪的积分误差可能导致偏航角估计漂移。
陀螺仪误差累积:陀螺仪测量的是角速度,要得到偏航角,需要将角速度积分。由于陀螺仪存在零漂、噪声和温度漂移等误差,这些误差在积分过程中会累积,使得偏航角估计产生较大的漂移。
虽然六轴传感器可能无法准确测量偏航角,但可以通过将其与磁罗盘(三轴磁场传感器)结合,形成九轴传感器(包括三轴加速度计、三轴磁罗盘和三轴陀螺仪),以提高偏航角估计的准确性。九轴传感器融合了磁场信息,为偏航角提供了一个稳定的参考方向,有助于减小陀螺仪误差对偏航角估计的影响。
陀螺仪解析代码
//加速度单位g,陀螺仪rad/s
void IMUupdate1(float gx, float gy, float gz, float ax, float ay, float az, float mx, float my, float mz)
{
float norm;
float vx, vy, vz;
float ex, ey, ez;
float hx, hy, hz, bx, bz;
float wx, wy, wz;
float halfT;
now_update = HAL_GetTick(); //ms
halfT = ((float)(now_update - last_update) / 2000.0f);
last_update = now_update;
// 测量正常化,把加计的三维向量转成单位向量。
norm = sqrt(ax*ax + ay*ay + az*az);
ax = ax / norm; //单位化
ay = ay / norm;
az = az / norm;
norm = sqrt(mx*mx + my*my + mz*mz);
mx = mx / norm;
my = my / norm;
mz = mz / norm;
// 这里计算得到的是地磁计在理论地磁坐标系下的机体上三个轴的分量
hx = 2*mx*(0.5 - q2*q2 - q3*q3) + 2*my*(q1*q2 - q0*q3) + 2*mz*(q1*q3 + q0*q2);
hy = 2*mx*(q1*q2 + q0*q3) + 2*my*(0.5 - q1*q1 - q3*q3) + 2*mz*(q2*q3 - q0*q1);
hz = 2*mx*(q1*q3 - q0*q2) + 2*my*(q2*q3 + q0*q1) + 2*mz*(0.5 - q1*q1 - q2*q2);
//bx计算的是当前航向角和磁北的夹角,也就是北天东坐标下的航向角
//当罗盘水平旋转的时候,航向角在0-360之间变化
bx = sqrt((hx*hx) + (hy*hy));
bz = hz;
//地磁计在n系下磁向量转换到b系下,反向使用DCM得到
wx = 2*bx*(0.5 - q2*q2 - q3*q3) + 2*bz*(q1*q3 - q0*q2);
wy = 2*bx*(q1*q2 - q0*q3) + 2*bz*(q0*q1 + q2*q3);
wz = 2*bx*(q0*q2 + q1*q3) + 2*bz*(0.5 - q1*q1 - q2*q2);
// 估计方向的重力,世界坐标系重力分向量是通过方向旋转矩阵的最后一列的三个元素乘上加速度就可以算出机体坐标系中的重力向量。
vx = 2*(q1*q3 - q0*q2);//由下向上方向的加速度在加速度计X分量
vy = 2*(q0*q1 + q2*q3);//由下向上方向的加速度在加速度计X分量
vz = q0*q0 - q1*q1 - q2*q2 + q3*q3;//由下向上方向的加速度在加速度计Z分量
//这个叉积向量仍旧是位于机体坐标系上的,而陀螺积分误差也是在机体坐标系,而且叉积的大小与陀螺积分误差成正比,正好拿来纠正陀螺。
//(你可以自己拿东西想象一下)由于陀螺是对机体直接积分,所以对陀螺的纠正量会直接体现在对机体坐标系的纠正。
// ex = (ay*vz - az*vy);
// ey = (az*vx - ax*vz);
// ez = (ax*vy - ay*vx);
ex = (ay*vz - az*vy) + (my*wz - mz*wy);
ey = (az*vx - ax*vz) + (mz*wx - mx*wz);
ez = (ax*vy - ay*vx) + (mx*wy - my*wx);
// 积分误差比例积分增益,计算陀螺仪测量的重力向量与估计方向的重力向量之间的误差。
// exInt = exInt + ex*Ki;
// eyInt = eyInt + ey*Ki;
// ezInt = ezInt + ez*Ki;
/* PI */
if(ex != 0.0f && ey != 0.0f && ez != 0.0f)
{
exInt = exInt + ex*Ki*halfT;
eyInt = eyInt + ey*Ki*halfT;
ezInt = ezInt + ez*Ki*halfT;
// 调整后的陀螺仪测量,使用叉积误差来进行比例-积分(PI)修正陀螺仪的零偏。将修正量乘以比例增益Kp,并加上之前计算的积分误差exInt、eyInt和ezInt。
// gx = gx + Kp*ex + exInt;
// gy = gy + Kp*ey + eyInt;
// gz = gz + Kp*ez + ezInt;
gx = gx + Kp*ex + exInt;
gy = gy + Kp*ey + eyInt;
gz = gz + Kp*ez + ezInt;
}
// 整合四元数率和正常化,根据陀螺仪的测量值和比例-积分修正值,对四元数进行更新。根据微分方程的离散化形式,将四元数的每个分量加上相应的微分项乘以采样周期的一半(halfT)。
q0 = q0 + (-q1*gx - q2*gy - q3*gz)*halfT;
q1 = q1 + (q0*gx + q2*gz - q3*gy)*halfT;
q2 = q2 + (q0*gy - q1*gz + q3*gx)*halfT;
q3 = q3 + (q0*gz + q1*gy - q2*gx)*halfT;
// 正常化四元数
norm = sqrt(q0*q0 + q1*q1 + q2*q2 + q3*q3);
q0 = q0 / norm;
q1 = q1 / norm;
q2 = q2 / norm;
q3 = q3 / norm;
// Pitch = asin(-2 * q1 * q3 + 2 * q0* q2)* 57.3; // pitch ,转换为度数
// Roll = atan2(2 * q2 * q3 + 2 * q0 * q1, -2 * q1 * q1 - 2 * q2* q2 + 1)* 57.3; // rollv
// Yaw = atan2(2*(q1*q2 + q0*q3),q0*q0+q1*q1-q2*q2-q3*q3) * 57.3; //偏移太大,等我找一个好用的
Pitch = asin(2 * q2 * q3 + 2 * q0* q1)* 57.3; // pitch ,转换为度数
Roll = atan2(-2 * q1 * q3 + 2 * q0 * q2, q0*q0-q1*q1-q2*q2+q3*q3)* 57.3; // rollv
Yaw = atan2(2*(q1*q2 - q0*q3),q0*q0-q1*q1+q2*q2-q3*q3) * 57.3; //偏移太大,等我找一个好用的
}
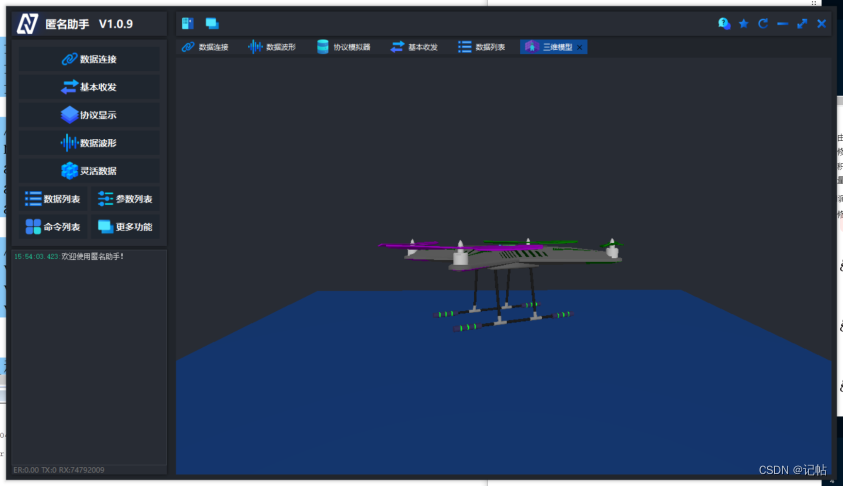
上报匿名助手能正常进行解析。