力扣刷题-二叉树-二叉树的所有路径

news2024/11/28 6:48:47

257 二叉树的所有路径

给定一个二叉树，返回所有从根节点到叶子节点的路径。
说明: 叶子节点是指没有子节点的节点。
示例:

思路

参考：
https://www.programmercarl.com/0257.%E4%BA%8C%E5%8F%89%E6%A0%91%E7%9A%84%E6%89%80%E6%9C%89%E8%B7%AF%E5%BE%84.html#%E6%80%9D%E8%B7%AF

迭代法

迭代法比较容易理解，就是去遍历每个节点，然后加入路径以及处理最终结果，需要采用栈stack来存储遍历结点，使用一个path_list来记录一条路径，使用result记录最终的结果。

class TreeNode(object):
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

# 方法一：采用迭代的方式 所谓迭代 就是去遍历到每个节点 相比递归更容易理解
# 时间复杂度:O(n) 因为是迭代到每个节点 空间复杂度: O(H) 两个栈 H为树的高度 平均是logn 最差为n 
class Solution(object):
    def binaryTreePaths(self, root):
        """
        :type root: TreeNode
        :rtype: List[str]
        """
        result = [] # 存储路径结果
        stack = [root] # 存储遍历结点 因为是路径 所以肯定是从根结点出发
        path_list = [str(root.val)] # 当前路径结点值
        while stack:
            node = stack.pop() # 当前节点（作为子树根节点的节点）
            path = path_list.pop() # 因为最终是路径(节点值构成) 所以先pop出来 下面再构成路径
            if node.left is None and node.right is None: # node为空节点 最开始为root 所以路径就是根节点
                result.append(path)
            if node.right:
                stack.append(node.right)
                path_list.append(path + "->" + str(node.right.val))
            if node.left:
                stack.append(node.left)
                path_list.append(path + "->" + str(node.left.val)) # 一次次迭代 串起来路径
        return result

递归法

这道题目要求从根节点到叶子的路径，所以需要前序遍历，这样才方便让父节点指向孩子节点，找到对应的路径。
在这道题目中将第一次涉及到回溯，因为我们要把路径记录下来，需要回溯来回退一个路径再进入另一个路径。
前序遍历以及回溯的过程如图：

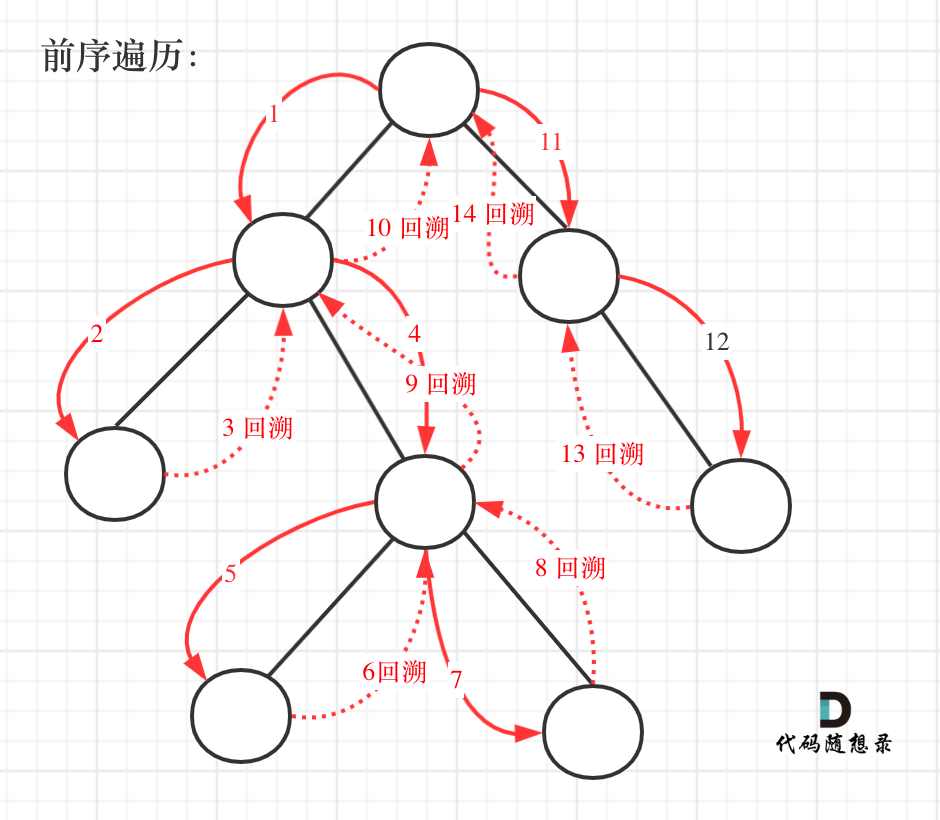
我们先使用递归的方式，来做前序遍历。要知道递归和回溯就是一家的，本题也需要回溯。

递归函数参数以及返回值

要传入根节点，记录每一条路径的path，和存放结果集的result，这里递归不需要返回值，代码如下：

# 递归部分的代码
def traversal(self, node, path_list, result): # 递归一 传入参数: 当前节点 路径暂存列表 最终结果列表

确定递归终止条件

在写递归的时候都习惯了这么写：

if node node:
	终止处理逻辑

但是本题的终止条件这样写会很麻烦，因为本题要找到叶子节点，就开始结束的处理逻辑了（把路径放进result里）。
那么什么时候算是找到了叶子节点？是当 cur不为空，其左右孩子都为空的时候，就找到叶子节点。
所以本题的终止条件是：

# 递归二 终止条件 此时是收获结果时候
if not node.left and not node.right:
    sPath = '->'.join(map(str, path_list)) # path_list中每个元素都先要转为str 所以用了map
    result.append(sPath) # 收获结果
    return # 结束

确定单层递归逻辑

因为是前序遍历，需要先处理中间节点，中间节点就是我们要记录路径上的节点，先放进path中。（注意和之后的不同，本题是写在终止处理的前面）
然后是递归和回溯的过程，上面说过没有判断cur是否为空，那么在这里递归的时候，如果为空就不进行下一层递归了。
所以递归前要加上判断语句，下面要递归的节点是否为空，如下：

# 左
if node.left:
    self.traversal(node.left, path_list, result) # 递归
    path_list.pop() # 回溯
# 右
if node.right:
    self.traversal(node.right, path_list, result) # 递归
    path_list.pop() # 回溯

注意：回溯和递归是一一对应的，有一个递归，就要有一个回溯所以是上面的写法
总体代码：

# 方法二：采用 递归 + 回溯 的方式
# 时间复杂度:O(n) 因为是迭代到每个节点 空间复杂度: O(H) 两个栈 H为树的高度 平均是logn 最差为n 
class Solution(object):
    def binaryTreePaths(self, root):
        """
        :type root: TreeNode
        :rtype: List[str]
        """
        result = []
        path_list = []
        if not root:
            return result 
        # result = self.traversal(root, path_list, result) 不需要返回 因为result自己会更新
        self.traversal(root, path_list, result)
        return result
    
    # 递归部分的代码
    def traversal(self, node, path_list, result): # 递归一 传入参数: 当前节点 路径暂存列表 最终结果列表
        path_list.append(node.val) # 中
        # 递归二 终止条件 此时是收获结果时候
        if not node.left and not node.right:
            sPath = '->'.join(map(str, path_list)) # path_list中每个元素都先要转为str 所以用了map
            result.append(sPath) # 收获结果
            return # 结束
        # 左
        if node.left:
            self.traversal(node.left, path_list, result) # 递归
            path_list.pop() # 回溯
        # 右
        if node.right:
            self.traversal(node.right, path_list, result) # 递归
            path_list.pop() # 回溯