此动态规划系列主要讲解大约10个系列【后续持续更新】
本篇讲解路径问题模型中的6道经典题,会在讲解题目同时给出AC代码
目录
1、不同路径
2、不同路径2
3、珠宝的最大价值
4、下降路径最小和
5、最小路径和
6、地下城游戏
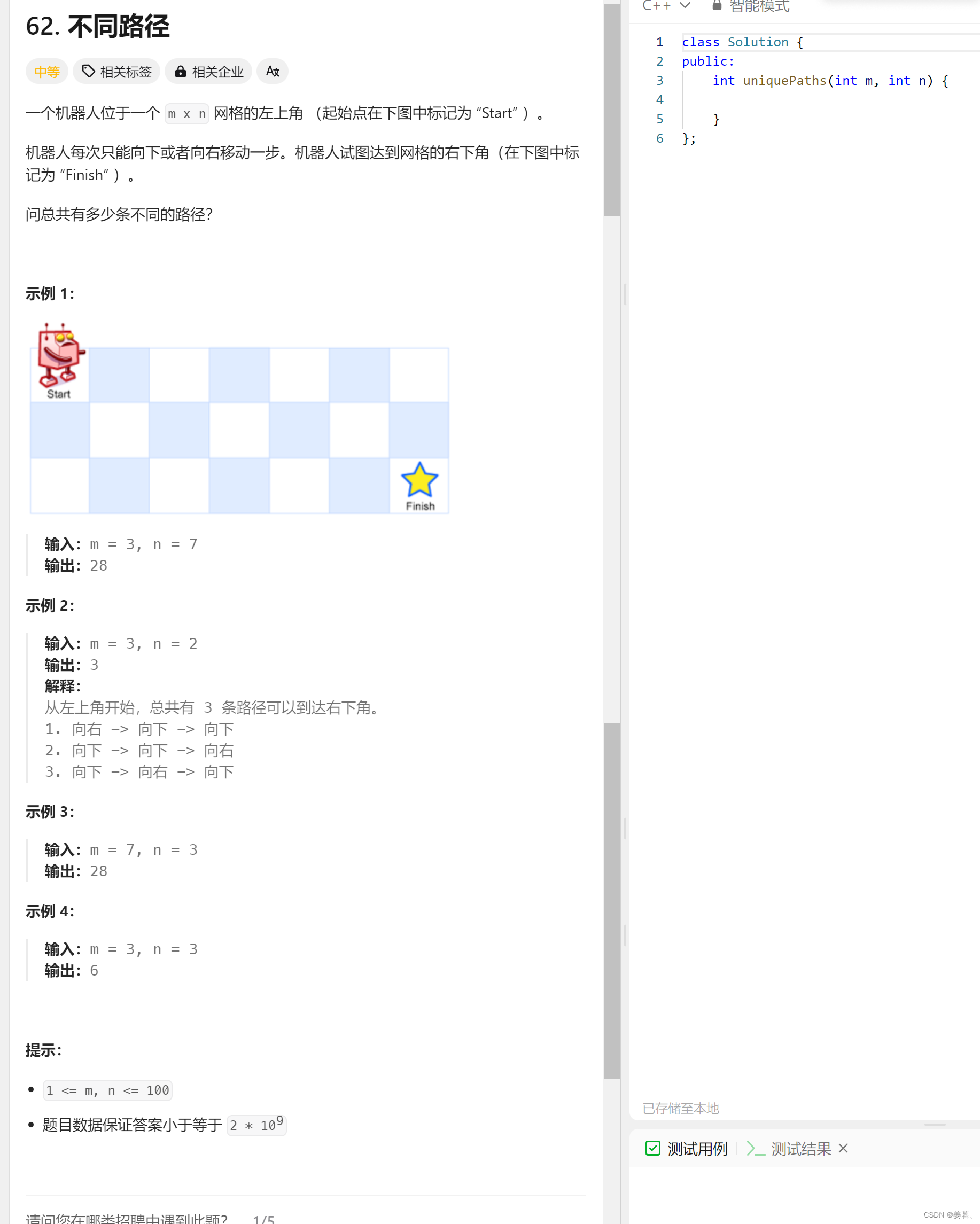
1、不同路径
class Solution {
public:
int uniquePaths(int m, int n) {
vector<vector<int>> dp(m + 1, vector<int> (n + 1));
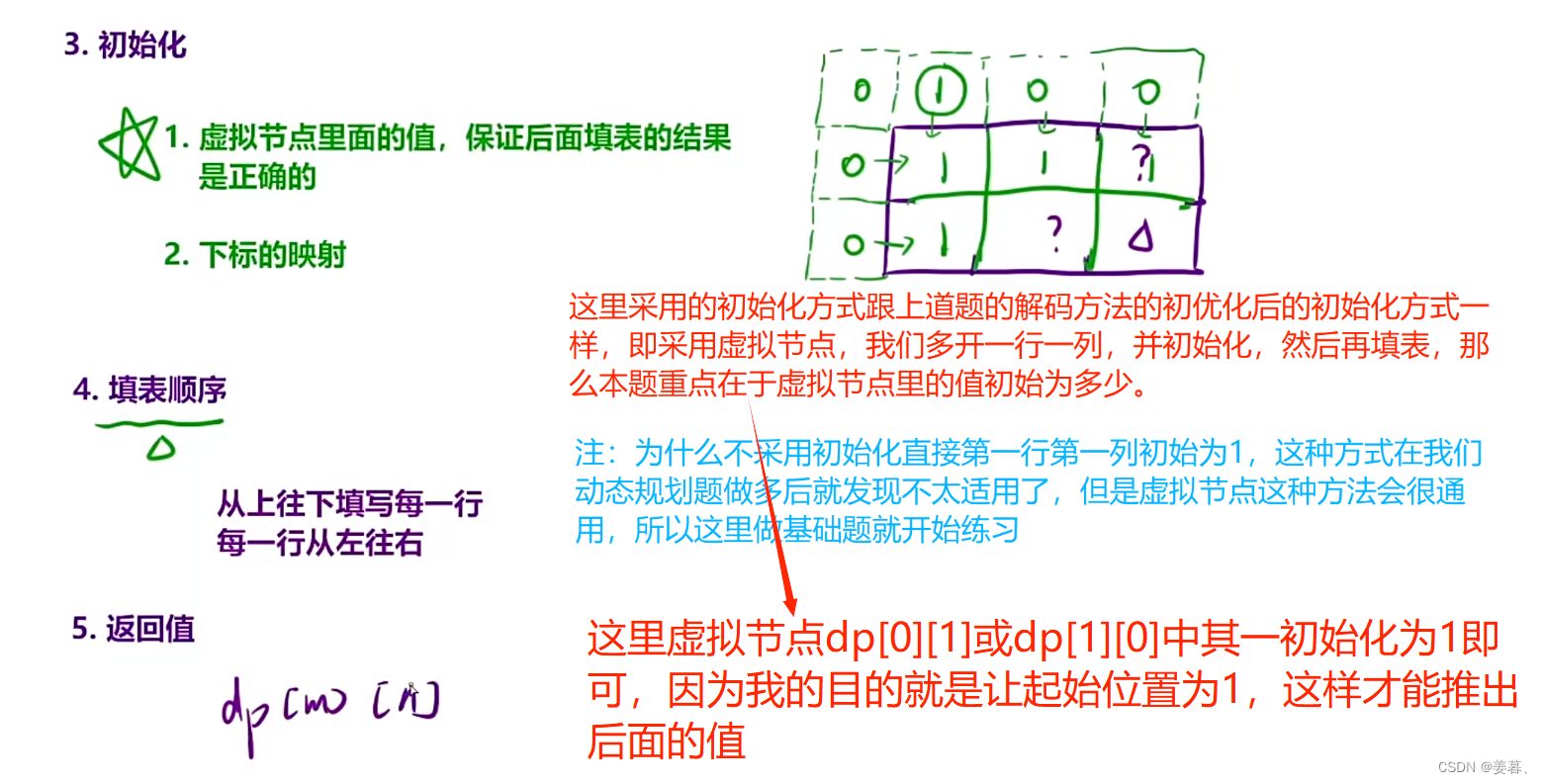
dp[0][1] = 1;//此位置的虚拟节点的初始化为1,方便后续计算
for (int i = 1; i <= m; i++)//从上到下遍历每一行
for (int j = 1; j <= n; j++)//从左到右填写每一行
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
return dp[m][n];
}
};2、不同路径2
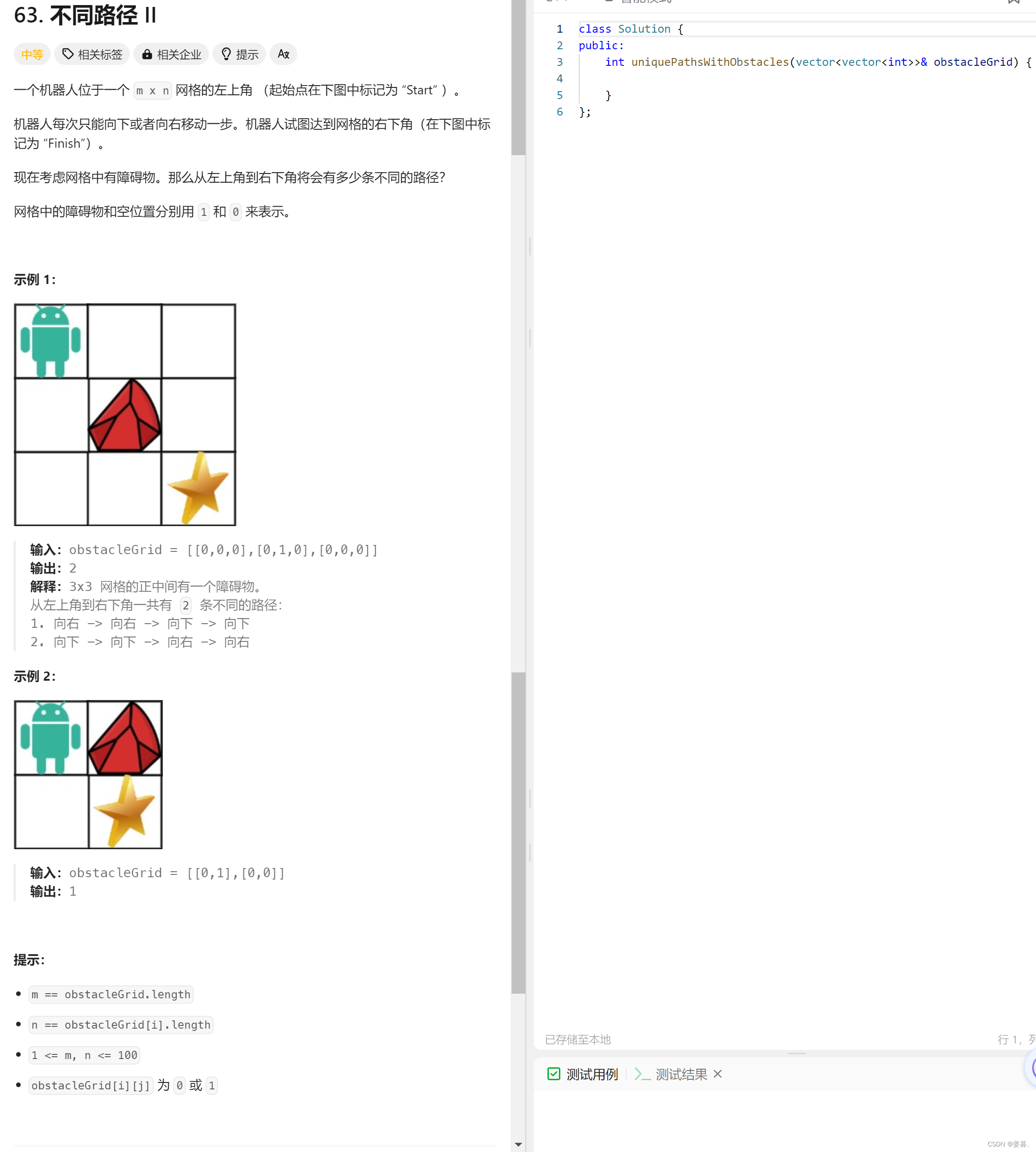

class Solution {
public:
int uniquePathsWithObstacles(vector<vector<int>>& ob) {
int m = ob.size(), n = ob[0].size();
vector<vector<int>> dp(m + 1, vector<int> (n + 1));
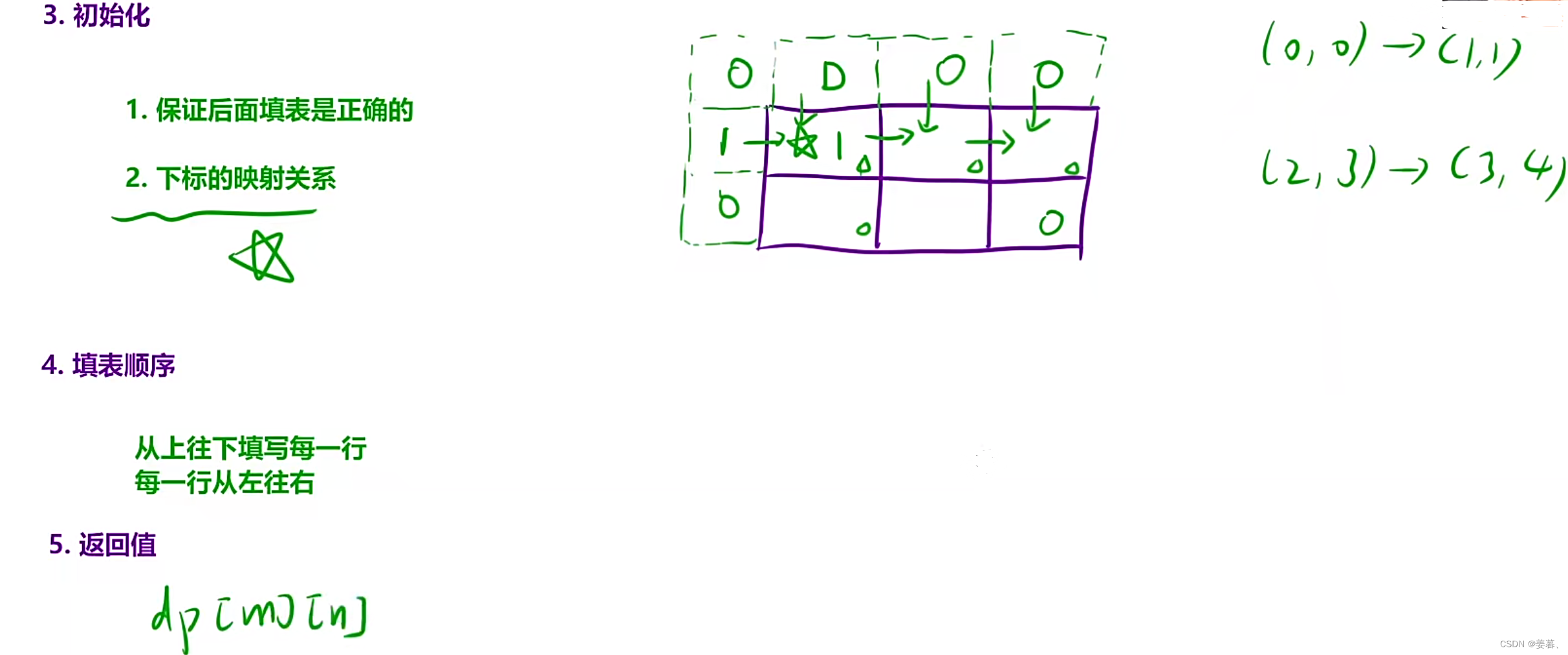
dp[1][0] = 1;//虚拟节点设置为1
for (int i = 1; i <= m; i++)
for(int j = 1; j <= n; j++)
if(ob[i - 1][j - 1] != 1)
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
return dp[m][n];
}
};3、珠宝的最大价值
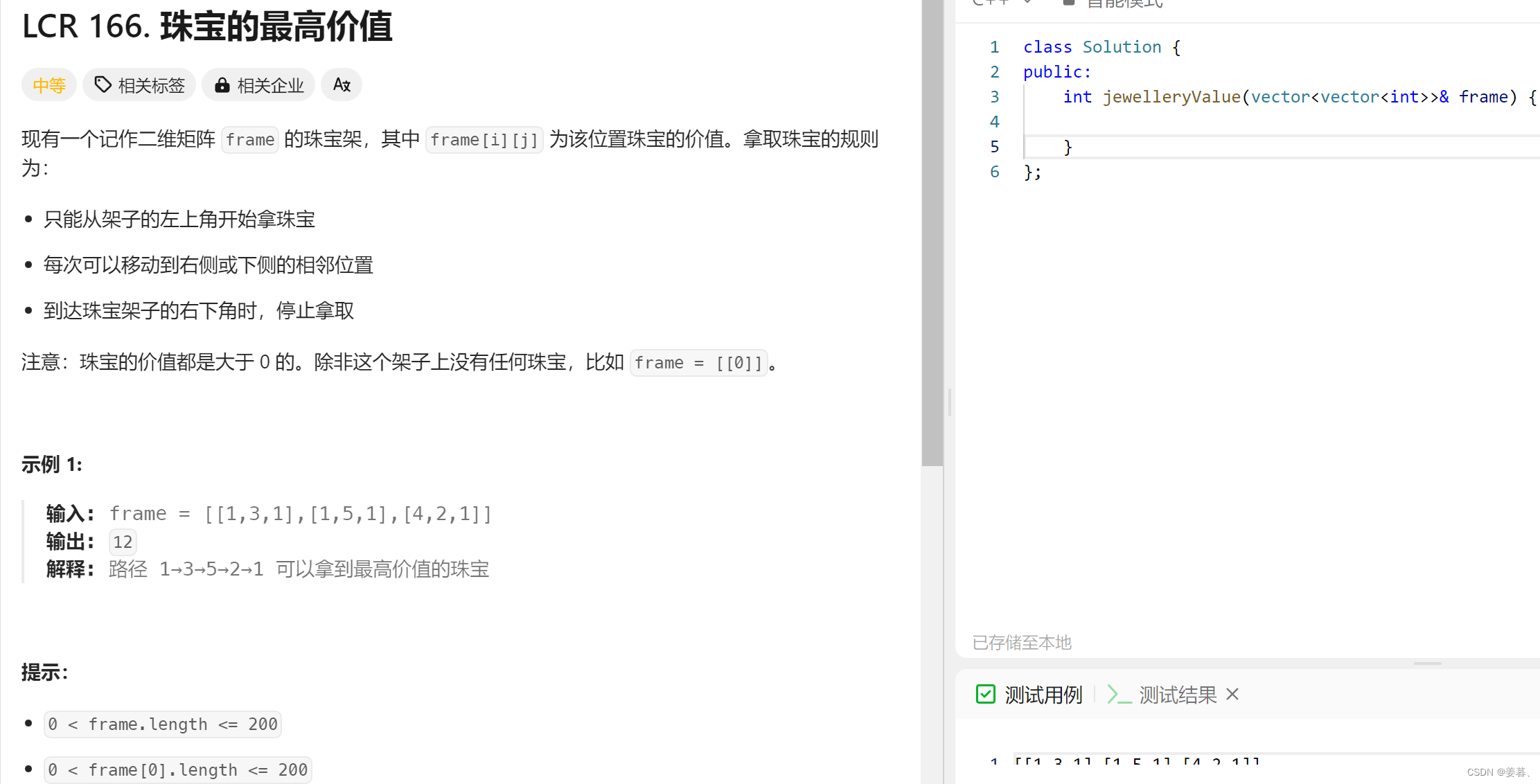


class Solution {
public:
int jewelleryValue(vector<vector<int>>& frame) {
int m = frame.size(), n = frame[0].size();
vector<vector<int>> dp(m + 1, vector<int>(n + 1));//会自动初始化为0
for(int i = 1; i <= m; i++)
for(int j = 1; j <= n; j++)
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]) + frame[i - 1][j - 1];
//因为设置虚拟节点,则frame[i-1][j-1],-1后拿到的才是原位置的价值
return dp[m][n];
}
};4、下降路径最小和



class Solution {
public:
int minFallingPathSum(vector<vector<int>>& matrix) {
int n = matrix.size();//方阵
vector<vector<int>> dp(n + 1, vector<int>(n + 2, INT_MAX));
//INT_MAX表示一个 32 位符号整数所能够表示的最大值
//初始化第一行
for (int i = 0; i < n + 2; i++) dp[0][i] = 0;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
dp[i][j] = min(dp[i - 1][j - 1], min(dp[i - 1][j], dp[i - 1][j + 1]))
+matrix[i - 1][j - 1];
int minimum = INT_MAX;
for (int i = 1; i <= n; i++)
minimum = min(minimum, dp[n][i]);
return minimum;
}
};5、最小路径和
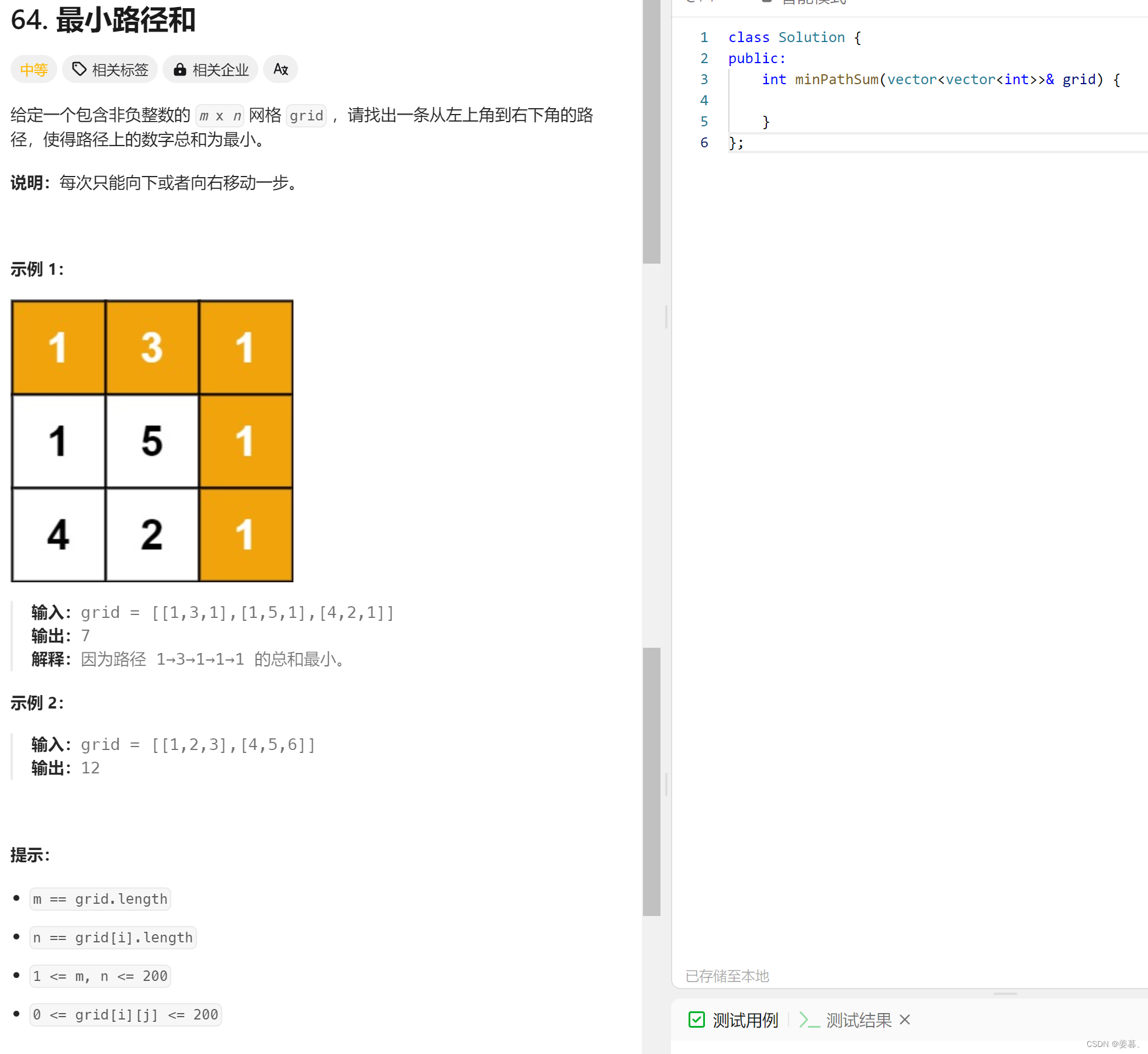

class Solution {
public:
int minPathSum(vector<vector<int>>& grid) {
int m = grid.size(), n = grid[0].size();
vector<vector<int>> dp(m + 1, vector<int>(n + 1, INT_MAX));
dp[0][1] = dp[1][0] = 0;
for (int i = 1; i <= m; i++)
for (int j = 1; j <= n; j++)
dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + grid[i - 1][j - 1];
return dp[m][n];
}
};6、地下城游戏
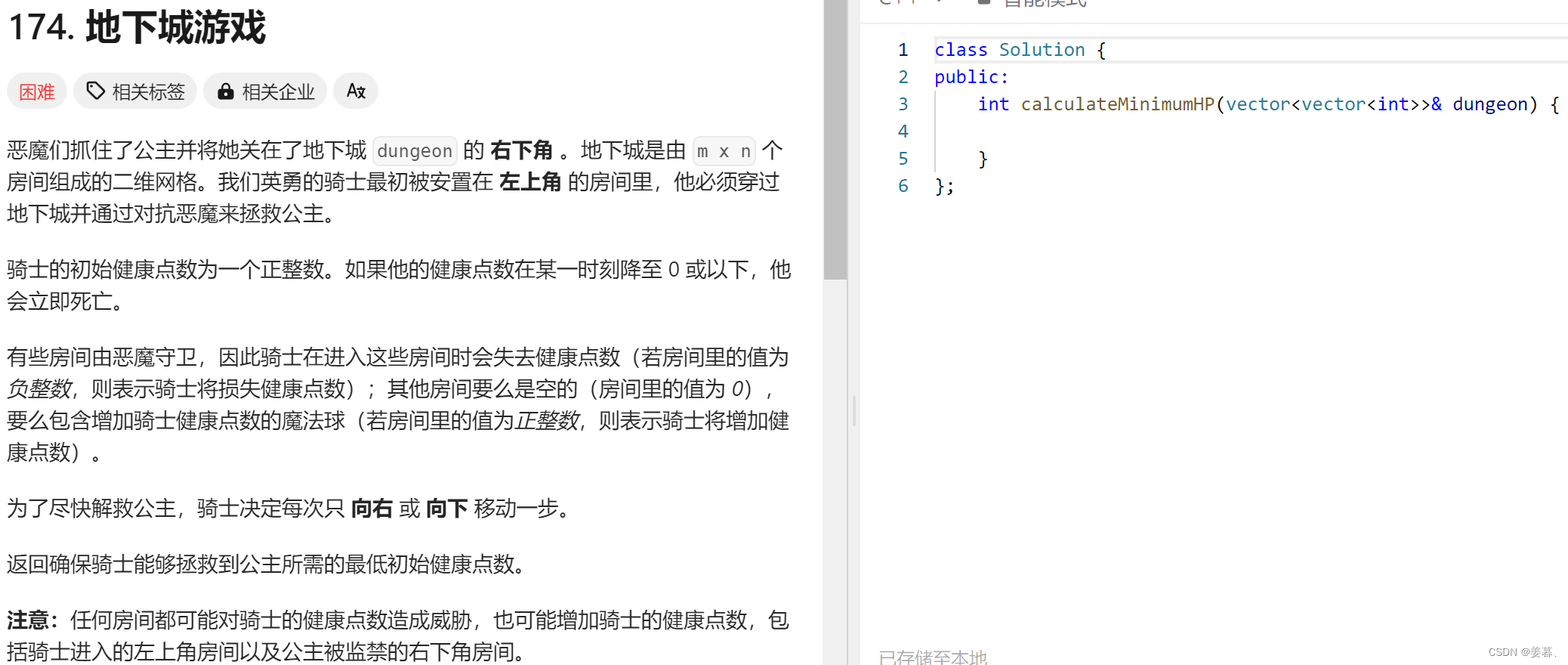


分析题目,模拟示例1:


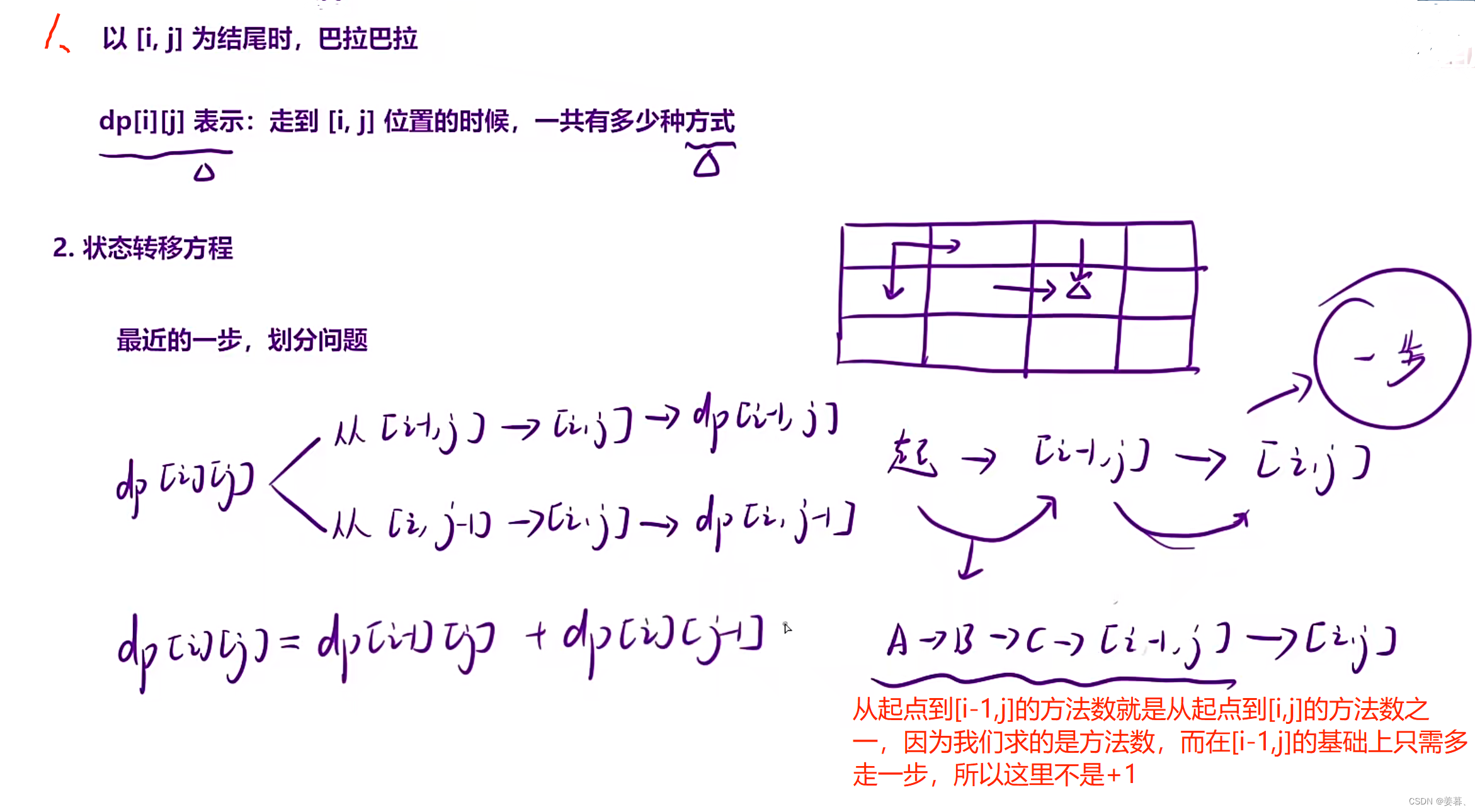
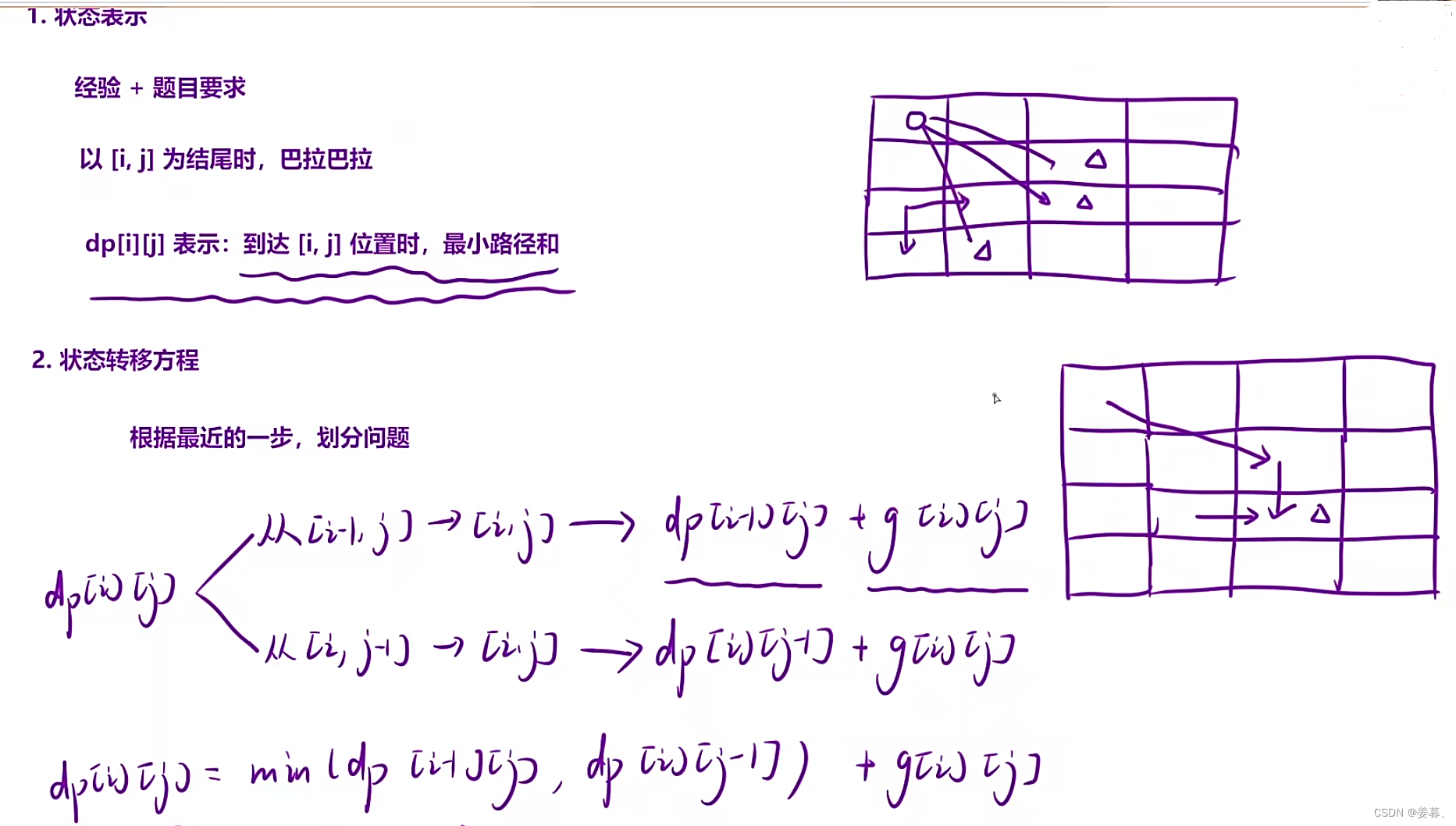
2、状态转移方程
怎样能从 ( i, j ) 位置正确进入到 ( i, j + 1 ) 位置呢?因为dp表里存的是从某个位置出发到终点时的最低血量. 故假设 ( i, j ) 位置此时最低初始血量为 X, 想要走出这个位置就需要先击败里面的恶魔 dungeon[i][j], 之后剩余血量 X + dungeon[i][j]【但也不排除dungeon[i][j]位置是血包,但不影响结果】 也就走出(i, j)位置后的血量必须>= ( i, j+1 ) 的最低初始血量 dp[i][j+1] 才能进入, 否则无法到达终点.当 X + dungeon[i][j] >= dp[i][j+1] 时才有机会到达终点. 题目要求最低初始血量, 取等时即可。
此时所需dp[i][j+1] - dungeon[i][j]
同理,从 ( i, j ) 位置到 ( i+1, j ) 位置后想要到达终点所需要的最低初始血量为
dp[i+1][j] - dungeon[i][j]
由于我们求的是从某点出发到终点的最低初始血量, 所以
状态转移方程:dp[i][j] = min(dp[i][j+1], dp[i+1][j] ) - dungeon[i][j]
注意:当 dungeon[i][j] 非常大时, dp[i][j] 最终会是一个< 0 的数。【但最低血量<=0都是会die的】
即( i, j ) 位置里面有个非常大的血包(dungeon[i][j]),此时从( i, j ) 位置走出去就是是负数了,可是按理说应该已经die了,不能走到下一位置了(dp[i][j+1],或dp[i+1][j])。那么这里就是没有考虑血包很大的问题,只是考虑了部分情况,按理说血包很大是可以走出去的,这是算是误判了,故必须保证在走出 ( i, j ) 位置后它的血量> 0。
因此最终需对dp[i][j]进行处理,dp[i][j] = max( 1, dp[i][j]
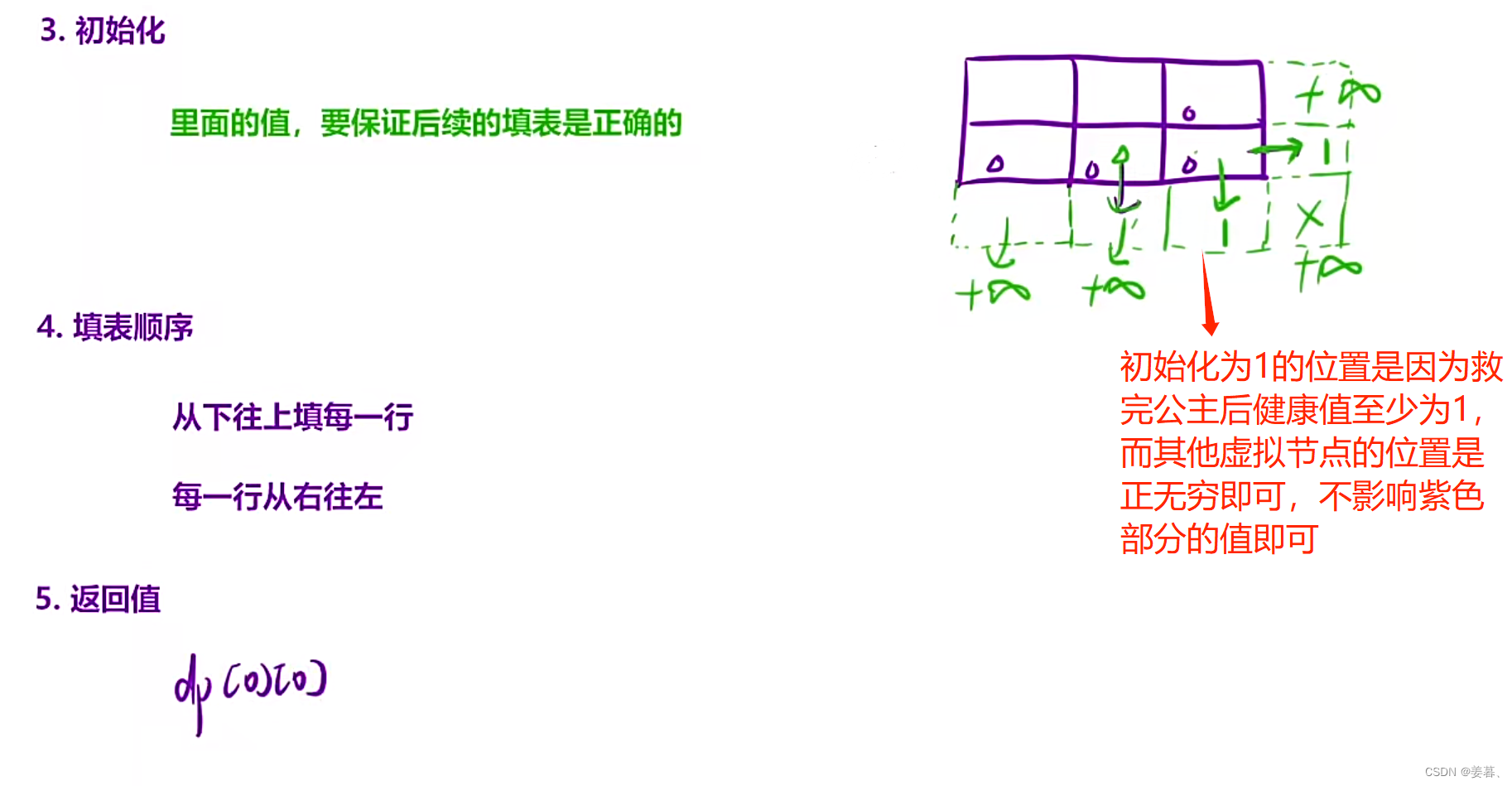
class Solution {
public:
int calculateMinimumHP(vector<vector<int>>& dungeon) {
int m = dungeon.size(), n = dungeon[0].size();
vector<vector<int>> dp(m + 1, vector<int>(n + 1, INT_MAX));
dp[m][n - 1] = dp[m - 1][n] = 1;
for (int i = m - 1; i >= 0; i--)
for (int j = n - 1; j >= 0; j--)
{
dp[i][j] = min(dp[i][j + 1], dp[i + 1][j]) - dungeon[i][j];
dp[i][j] = max(1, dp[i][j]);
}
return dp[0][0];
}
};