力扣刷题-二叉树-平衡二叉树

news2024/11/29 12:51:09

110 平衡二叉树

给定一个二叉树，判断它是否是高度平衡的二叉树。
本题中，一棵高度平衡二叉树定义为：一个二叉树每个节点的左右两个子树的高度差的绝对值不超过1。
示例 1:
给定二叉树 [3,9,20,null,null,15,7]

返回 true 。
给定二叉树 [1,2,2,3,3,null,null,4,4]

返回 false 。

思路

参考：
https://www.programmercarl.com/0110.%E5%B9%B3%E8%A1%A1%E4%BA%8C%E5%8F%89%E6%A0%91.html#%E6%9C%AC%E9%A2%98%E6%80%9D%E8%B7%AF
强调一下概念：

二叉树节点的深度：指从根节点到该节点的最长简单路径边的条数。
二叉树节点的高度：指从该节点到叶子节点的最长简单路径边的条数。

但leetcode中强调的深度和高度很明显是按照节点来计算的，如图：

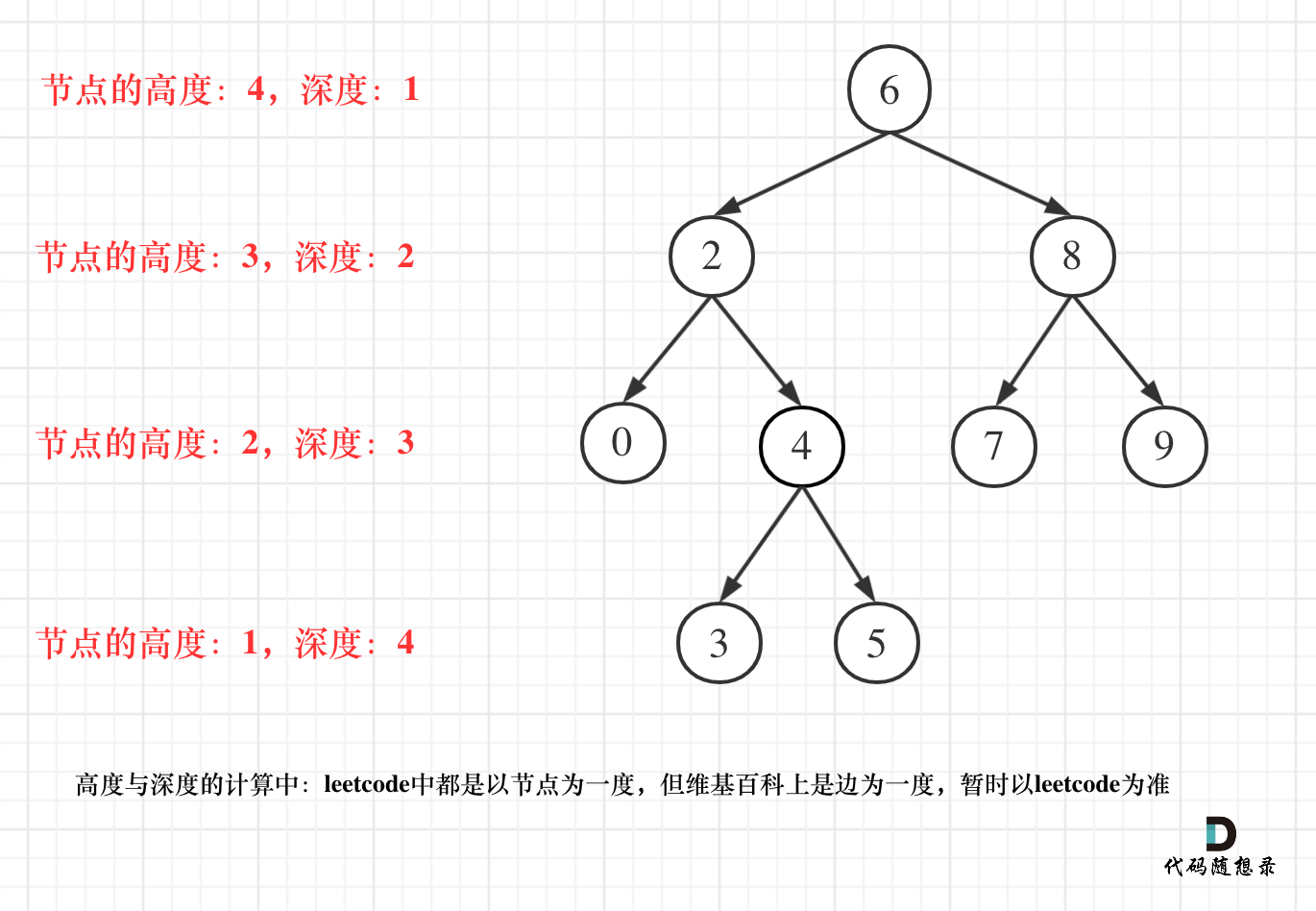
注意：leetcode的题目中都是以节点为一度，即根节点深度是1。
本题思路：

递归

此时大家应该明白了既然要求比较高度，必然是要后序遍历。
递归三步曲分析：

明确递归函数的参数和返回值

参数：当前传入节点。返回值：以当前传入节点为根节点的树的高度。
那么如何标记左右子树是否差值大于1呢？
如果当前传入节点为根节点的二叉树已经不是二叉平衡树了，还返回高度的话就没有意义了。
所以如果已经不是二叉平衡树了，**可以返回-1 **来标记已经不符合平衡树的规则了。

def get_height(self, node): # 递归一: 传入当前节点(以当前节点为根节点) 返回值为int 就是子树高度

明确终止条件

递归的过程中依然是遇到空节点了为终止，返回0，表示当前节点为根节点的树高度为0

if not node:
    return 0 # 递归二：如果节点不存在 显然该节点的高度为0

明确单层递归的逻辑

如何判断以当前传入节点为根节点的二叉树是否是平衡二叉树呢？当然是其左子树高度和其右子树高度的差值。
分别求出其左右子树的高度，然后如果差值小于等于1，则返回当前二叉树的高度，否则返回-1，表示已经不是二叉平衡树了。
严格按照左右中的写法会更加清晰

# 单层递归逻辑 后序遍历思想 左右中 先分别求出其左右子树的高度
leftheight = self.get_height(node.left)
if leftheight == -1: # 采用-1表示非平衡了 左
    return -1
rightheight = self.get_height(node.right)
if rightheight == -1: # 采用-1表示非平衡了 右
    return -1
# 中
# 求左子树高度和其右子树高度的差值。分别求出其左右子树的高度，然后如果差值小于等于1，则返回当前二叉树的高度，否则返回-1
if abs(leftheight-rightheight) > 1: # 差值大于1
    return -1
else:
    return 1 + max(leftheight, rightheight) # 一棵子树高度

最终的 get_height 代码：

def get_height(self, node): # 递归一: 传入当前节点(以当前节点为根节点) 返回值为int 就是子树高度
    if not node:
        return 0 # 递归二：如果节点不存在 显然该节点的高度为0 
    # 单层递归逻辑 后序遍历思想 左右中 先分别求出其左右子树的高度
    leftheight = self.get_height(node.left)
    if leftheight == -1: # 采用-1表示非平衡了 左
        return -1
    rightheight = self.get_height(node.right)
    if rightheight == -1: # 采用-1表示非平衡了 右
        return -1
    # 中
    # 求左子树高度和其右子树高度的差值。分别求出其左右子树的高度，然后如果差值小于等于1，则返回当前二叉树的高度，否则返回-1
    if abs(leftheight-rightheight) > 1: # 差值大于1
        return -1
    else:
        return 1 + max(leftheight, rightheight) # 一棵子树高度

最后本题整体递归代码如下：

class TreeNode(object):
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class Solution(object):
    def isBalanced(self, root):
        """
        :type root: TreeNode
        :rtype: bool
        """
        # if not root:
        #     return True 下面的递归函数 已经包含了 
        if self.get_height(root) != -1: # 采用 -1 来标识
            return True
        else:
            return False 
    
    def get_height(self, node): # 递归一: 传入当前节点(以当前节点为根节点) 返回值为int 就是子树高度
        if not node:
            return 0 # 递归二：如果节点不存在 显然该节点的高度为0 
        # 单层递归逻辑 后序遍历思想 左右中 先分别求出其左右子树的高度
        leftheight = self.get_height(node.left)
        if leftheight == -1: # 采用-1表示非平衡了 左
            return -1
        rightheight = self.get_height(node.right)
        if rightheight == -1: # 采用-1表示非平衡了 右
            return -1
        # 中
        # 求左子树高度和其右子树高度的差值。分别求出其左右子树的高度，然后如果差值小于等于1，则返回当前二叉树的高度，否则返回-1
        if abs(leftheight-rightheight) > 1: # 差值大于1
            return -1
        else:
            return 1 + max(leftheight, rightheight) # 一棵子树高度