【数据结构】八大排序之直接插入排序算法

news2024/10/6 8:39:55

🦄个人主页:修修修也

🎏所属专栏:数据结构

⚙️操作环境:Visual Studio 2022

一.直接插入排序简介及思路

直接插入排序(Straight Insertion Sort)是一种简单直观的插入排序算法.

它的基本操作是:

将一个数据插入到已经排好的有序表中,从而得到一个新的,数据数增1的有序表.
直到所有的数据插入完为止,得到一个新的有序序列.

在实际生活中,我们玩扑克牌时就使用了插入排序的思想:

算法动图演示如下:

二.直接插入排序的代码实现

算法实现步骤:(以升序为例)

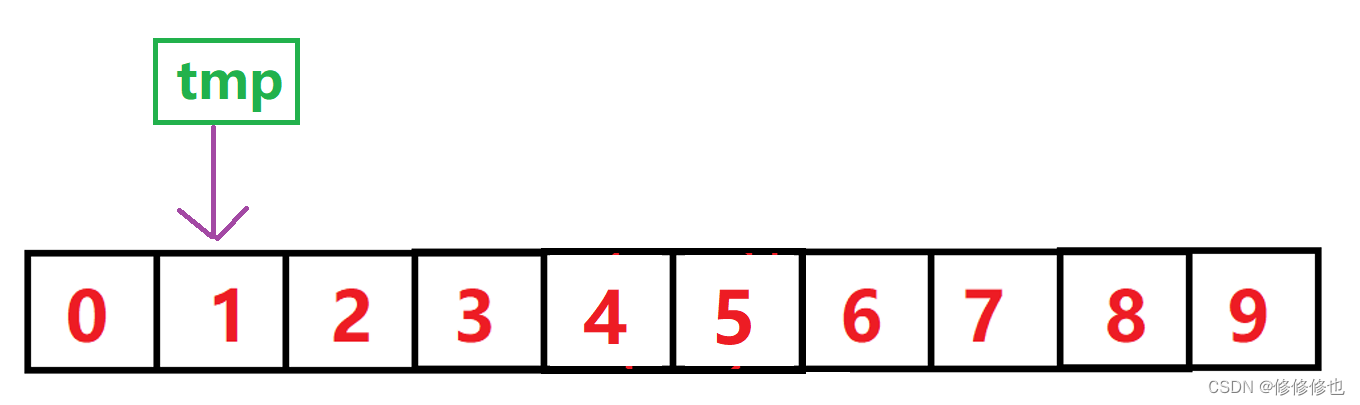
当表中只有第一个数据的时候它是一定有序的,因此我们从第二个元素开始向前面的有序表"插入"数据.
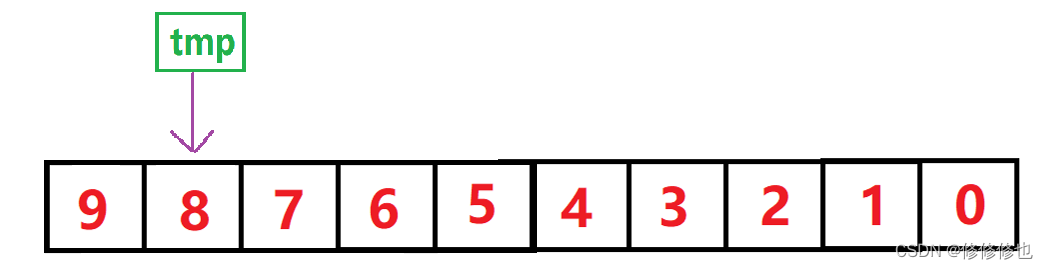
具体插入方式,使用tmp记录下当前待插入元素,然后tmp从后向前与有序表中的元素逐一比对,如果tmp小于比对元素,则比对元素向后挪动一个位置.
直到tmp不小于比对元素时,将tmp插入到比对元素后面.
循环将数据向前插入,直到将待排数组的所有数据元素都插入进有序表,排序完成.

清楚了逻辑和概念后,我们的代码实现就比较简单了.代码如下:

//插入排序(升序
void InsertSort(int* a, int n)
{
	for (int i = 1; i < n; i++)
	{
		int end = i - 1;
		int tmp = a[i];
		//将tmp插入到[0,end]这个有序表的区间里

		while (end >= 0)
		{
			if (tmp < a[end])  //如果tmp小于比对元素,将比对元素向后挪
			{
				a[end + 1] = a[end];
				end--;
			}
			else       //如果tmp不小于比对元素,将tmp插入到比对元素后面
			{
				break;
			}
		}
		a[end + 1] = tmp;
	}
}

三.直接插入排序的时间复杂度分析

📌最好情况时间复杂度

直接排序的最好情况是每个tmp向前插入时都发现自己恰好不小于前面有序表中的最后一个元素,这时就直接将自己放在自己原本的地方就可以继续向前插入下一个元素了,即数组完全顺序的情况:

易得此时的:

算法执行次数为: $n-1$
算法时间复杂度为: $O(n)$

📌最坏情况时间复杂度

直接插入的最坏情况是遇到每一个tmp都直到比对到前面有序表的0号位置才插入,即数组完全逆序的情况:

此时算法每趟的交换次数累加起来就是1 + 2 + ...... +(n-2)+(n-1),可以发现当算法执行结束,所有次数累加起来恰好是一个等差数列,我们利用求和公式可得:

算法执行总次数为: $\frac{1}{2}n^{2}-\frac{1}{2}n$
算法时间复杂度为: $O(n^{2})$

四.直接插入排序的优化

我们通过对前面直接插入排序的分析可以发现,当数组整体完全逆序时:

算法的执行总次数为: $(1+2+......+n-1)$

算法的执行总次数为: $\frac{1}{2}n^{2}-\frac{1}{2}n$

但是如果我们面对的是前后两部分分别逆序的数组时:

算法的执行总次数为: $(1+2+...+\frac{n}{2}-1)+(1+2+...+\frac{n}{2}-1)$

算法的执行总次数为: $\frac{1}{4}n^2-\frac{1}{2}n$

此时算法的效率就提高了: $\frac{1}{4}n^2$

如果我们再分为前后四部分逆序的数组时:

算法的执行总次数为: $(1+2+...+\frac{n}{4}-1)*4$

算法的执行总次数为: $\frac{1}{8}n^2-\frac{1}{2}n$

此时算法的效率又提高了: $\frac{1}{8}n^2$

通过前面的分析,我们可以发现,随着我们分的部分的增加,算法的执行次数在有规律的减少:

分成k部分与算法执行总次数有如下关系: $\frac{1}{k}*\frac{1}{2}n^2-\frac{1}{2}n$

如果我们令k无限大,此时算法的执行次数就可以忽略n^2项,而只剩下1/2n项了

其实k无限大的情况,就是数组被分为只有前后两个元素逆序的情况:

这种情况下,算法的执行总次数:(1+1+......+1+1)

算法的执行总次数: $\frac{n}{2}$

通过上面的分析,我们可以得到一个结论:

当数组元素越接近基本有序,直接插入排序算法的时间复杂度就会越低.

那么我们是不是可以在正式进行插入排序之前将数组元素先简单"预排序"一下呢,即在预排序中,我们尽量将大一些的元素放在数组靠后的位置,小一些的元素放在数组靠前的位置,这样再进行直接插入排序就能使效率提高很多.

如果你能够理解这一直接插入排序算法的优化思路,那么恭喜你,你已经理解了希尔排序的思想,接下来我会在另一篇博客中,详细介绍怎样通过这一思路优化直接插入排序算法,最终构造出非常著名的希尔排序算法.

感兴趣的朋友可以直接点击下方文章链接查看希尔排序算法的相关内容:

【数据结构】八大排序之希尔排序https://blog.csdn.net/weixin_72357342/article/details/135043566

结语

希望这篇直接插入排序算法详解能对大家有所帮助,欢迎大佬们留言或私信与我交流.

有关更多排序相关知识可以移步:

【数据结构】八大排序算法https://blog.csdn.net/weixin_72357342/article/details/135038495?csdn_share_tail=%7B%22type%22%3A%22blog%22%2C%22rType%22%3A%22article%22%2C%22rId%22%3A%22135038495%22%2C%22source%22%3A%22weixin_72357342%22%7D&fromshare=blogdetail

学海漫浩浩,我亦苦作舟!关注我,大家一起学习,一起进步!