491. 递增子序列
题目连接:491. 递增子序列
思路:将问题抽象为树形结构,使用回溯法。本题求自增子序列,是不能对原数组进行排序的,排完序的数组都是自增子序列了。所以不能使用之前的去重逻辑!

HashSet是记录本层元素是否重复使用,新的一层set都会重新定义(清空),所以要知道set只负责本层!
class Solution {
private List<List<Integer>> res = new ArrayList<>();
private List<Integer> path = new ArrayList<>();
public List<List<Integer>> findSubsequences(int[] nums) {
backtracking(nums, 0);
return res;
}
// 回溯算法主函数
private void backtracking(int[] nums, int start) {
if (path.size() >= 2) {
// 找到一个合法答案
res.add(new ArrayList<>(path));
}
// 使用set来对本层元素进行去重
HashSet<Integer> used = new HashSet<>();
// 回溯算法标准框架
for (int i = start; i < nums.length; i++) {
// 保证集合中元素都是递增顺序
if (!path.isEmpty() && path.get(path.size() - 1) > nums[i]) {
continue;
}
// 保证不要重复使用相同的元素
if (used.contains(nums[i])) {
continue;
}
// 选择 nums[i]
// 记录这个元素在本层用过了,本层后面不能再用了
used.add(nums[i]);
path.add(nums[i]);
// 递归遍历下一层回溯树
backtracking(nums, i + 1);
// 撤销选择 nums[i]
path.remove(path.size() - 1);
}
}
}
46. 全排列
题目链接:46. 全排列
思路:将问题抽象成树形结构,使用回溯法搜索结果。
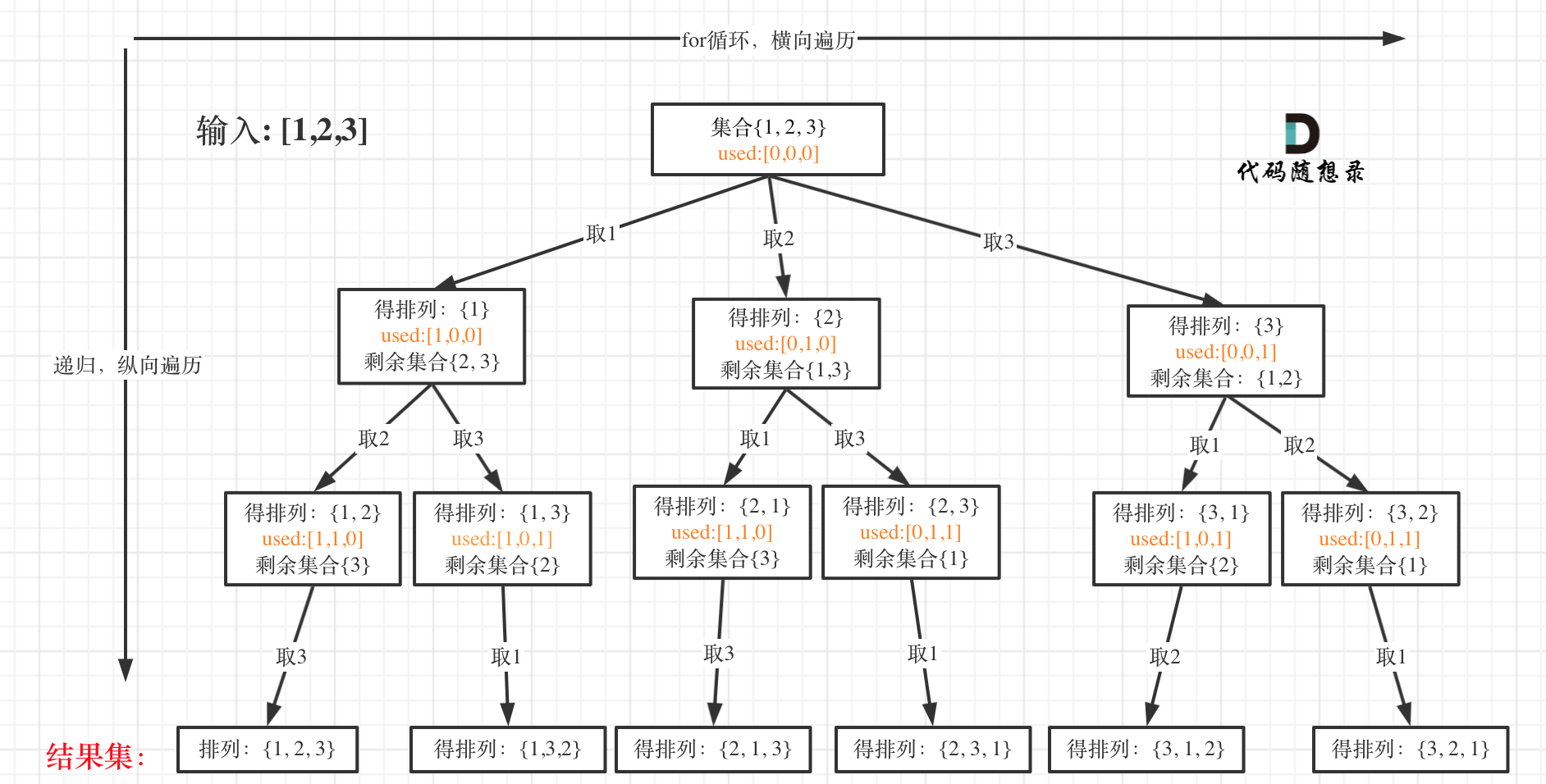
此时可以感受出排列问题的不同:
- 每层都是从0开始搜索而不是start
- 需要used数组记录path里都放了哪些元素了
class Solution {
private List<List<Integer>> res = new ArrayList<>();
private List<Integer> path = new ArrayList<>();
/* 主函数,输入一组不重复的数字,返回它们的全排列 */
public List<List<Integer>> permute(int[] nums) {
// 「路径」中的元素会被标记为 true,避免重复使用
boolean[] used = new boolean[nums.length];
Arrays.fill(used, false);
backtracking(nums, used);
return res;
}
// 路径:记录在 path 中
// 选择列表:nums 中不存在于 path 的那些元素(used[i] 为 false)
// 结束条件:nums 中的元素全都在 path 中出现
private void backtracking(int[] nums, boolean[] used) {
// 触发结束条件
if (path.size() == nums.length) {
res.add(new ArrayList(path));
return;
}
for (int i = 0; i < nums.length; i++) {
// 排除不合法的选择
if (used[i]) {
// nums[i] 已经在 path 中,跳过
continue;
}
// 做选择
path.add(nums[i]);
used[i] = true;
// 进入下一层决策树
backtracking(nums, used);
// 取消选择
used[i] = false;
path.remove(path.size() - 1);
}
}
}
另一种解法:
class Solution {
private List<List<Integer>> res = new ArrayList<>();
private List<Integer> path = new ArrayList<>();
// 通过判断path中是否存在数字,排除已经选择的数字
public List<List<Integer>> permute(int[] nums) {
backtracking(nums);
return res;
}
private void backtracking(int[] nums) {
if (path.size() == nums.length) {
res.add(new ArrayList<>(path));
return;
}
for (int i = 0; i < nums.length; i++) {
// 如果path中已有,则跳过
if (path.contains(nums[i])) continue;
path.add(nums[i]);
backtracking(nums);
path.remove(path.size() - 1);
}
}
}
47. 全排列II
题目链接:47. 全排列 II
思路:将问题抽象成树形结构,同一树层需要去重,同一树枝上也要判断是否使用过(注意这里是如何判断的)

一般来说:组合问题和排列问题是在树形结构的叶子节点上收集结果,而子集问题就是取树上所有节点的结果。
对于排列问题,树层上去重和树枝上去重,都是可以的,但是树层上去重效率更高!
class Solution {
private List<List<Integer>> res = new ArrayList<>();
private List<Integer> path = new ArrayList<>();
public List<List<Integer>> permuteUnique(int[] nums) {
// 先排序,让相同的元素靠在一起
Arrays.sort(nums);
boolean[] used = new boolean[nums.length];
Arrays.fill(used, false);
backtracking(nums, used);
return res;
}
private void backtracking(int[] nums, boolean[] used) {
if (path.size() == nums.length) {
res.add(new ArrayList<>(path));
return;
}
for (int i = 0; i < nums.length; i++) {
// used[i - 1] == true,说明同⼀树枝nums[i - 1]使⽤过
// used[i - 1] == false,说明同⼀树层nums[i - 1]使⽤过
// 如果同⼀树层nums[i - 1]使⽤过则直接跳过
if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
continue;
}
// 如果同⼀树枝nums[i]没使⽤过开始处理
if (used[i] == false) {
// 标记同⼀树枝nums[i]使⽤过,防止同一树枝重复使用
path.add(nums[i]);
used[i] = true;
backtracking(nums, used);
// 回溯,说明同⼀树层nums[i]使⽤过,防止下一树层重复
used[i] = false;// 回溯
path.remove(path.size() - 1);
}
}
}
}