【人工智能】实验二: 洗衣机模糊推理系统实验与基础知识

news2024/9/19 13:24:49

实验二: 洗衣机模糊推理系统实验

实验目的

理解模糊逻辑推理的原理及特点，熟练应用模糊推理。

实验内容

设计洗衣机洗涤时间的模糊控制。

实验要求

已知人的操作经验为：

  • “污泥越多，油脂越多，洗涤时间越长”；
  • “污泥适中,油脂适中,洗涤时间适中”；
  • “污泥越少，油脂越少，洗涤时间越短”。

模糊控制规则如表1所示：

xyz
SDNGVS
SDMGM
SDLGL
MDNGS
MDMGM
MDLGL
LDNGM
LDMGL
LDLGVL

其中：

  • SD(污泥少)、MD(污泥中)、LD(污泥多)、NG(油脂少)、MG(油脂中)、LG(油脂多)、VS(洗涤时间很短)、S(洗涤时间短)、M(洗涤时间中等)、L(洗涤时间长)、VL(洗涤时间很长)。

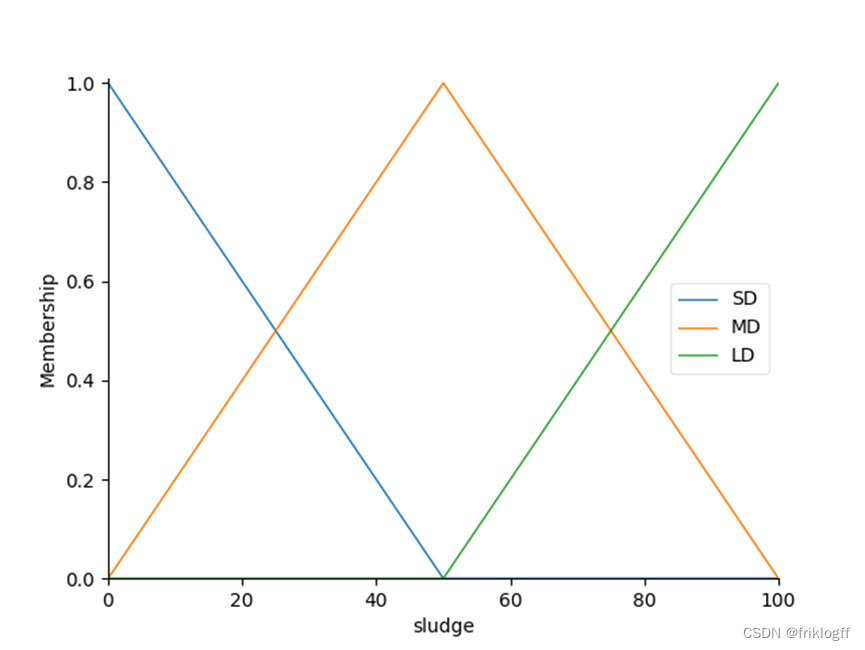
1. 污泥隶属函数

# 污泥隶属函数
sludge['SD'] = fuzz.trimf(sludge.universe, [0, 0, 50])
sludge['MD'] = fuzz.trimf(sludge.universe, [0, 50, 100])
sludge['LD'] = fuzz.trimf(sludge.universe, [50, 100, 100])

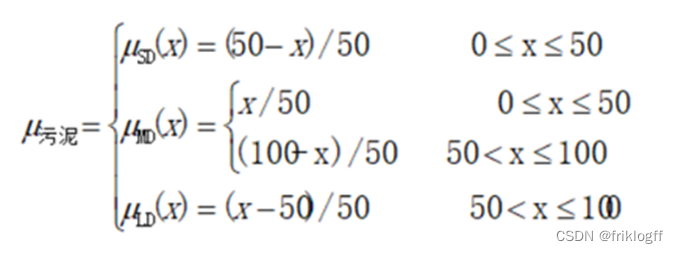
在这里插入图片描述
在这里插入图片描述

2. 油脂隶属函数

# 油脂隶属函数
grease['NG'] = fuzz.trimf(grease.universe, [0, 0, 50])
grease['MG'] = fuzz.trimf(grease.universe, [0, 50, 100])
grease['LG'] = fuzz.trimf(grease.universe, [50, 100, 100])

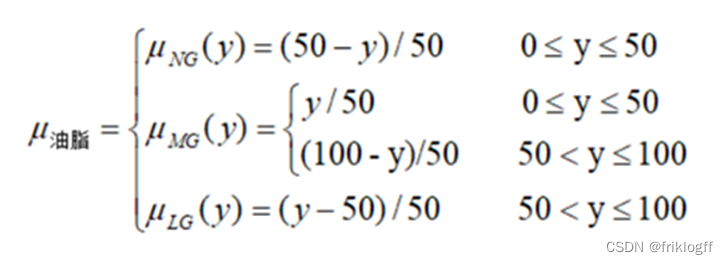
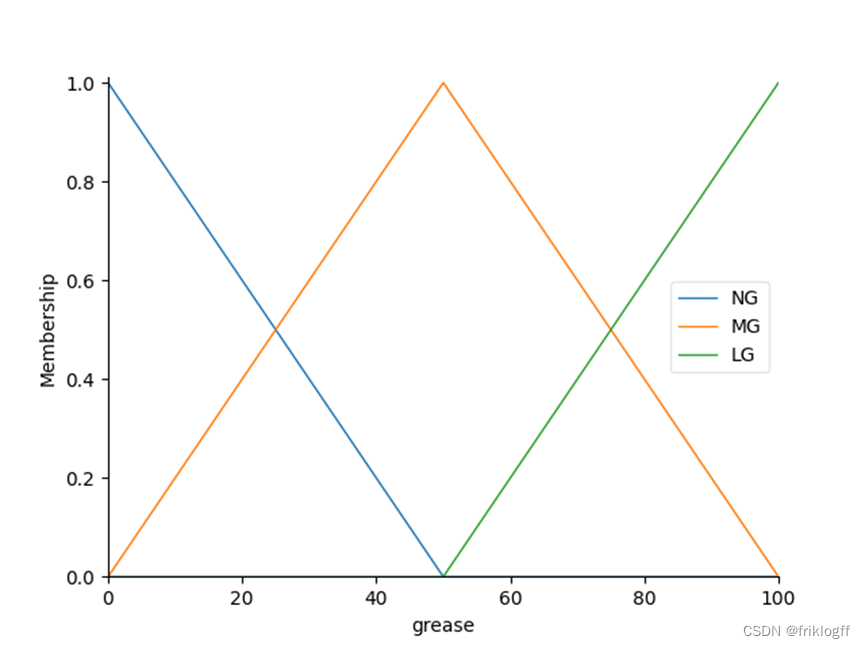
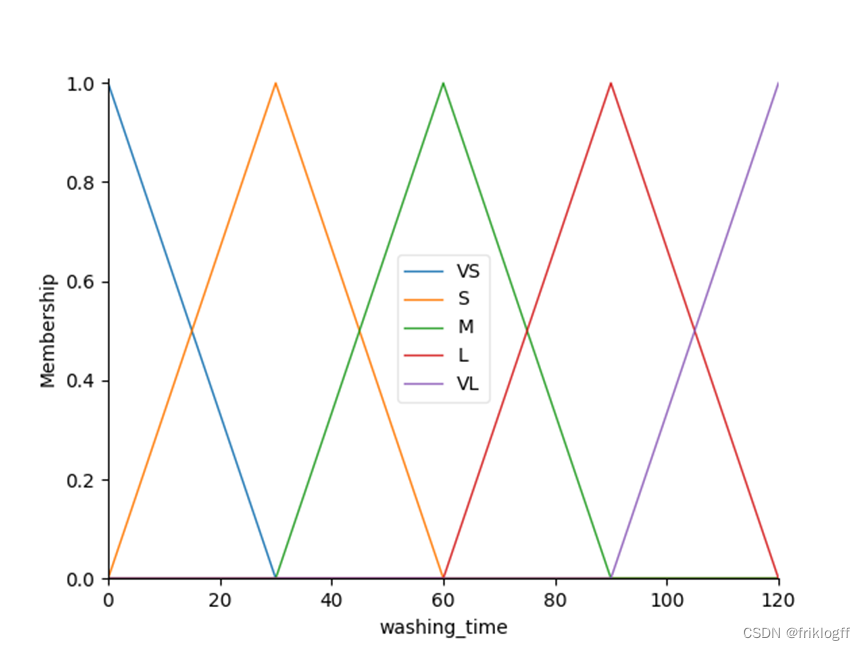
在这里插入图片描述
在这里插入图片描述

3. 洗涤时间隶属度函数

# 洗涤时间隶属度函数
washing_time['VS'] = fuzz.trimf(washing_time.universe, [0, 0, 30])
washing_time['S'] = fuzz.trimf(washing_time.universe, [0, 30, 60])
washing_time['M'] = fuzz.trimf(washing_time.universe, [30, 60, 90])
washing_time['L'] = fuzz.trimf(washing_time.universe, [60, 90, 120])
washing_time['VL'] = fuzz.trimf(washing_time.universe, [90, 120, 120])

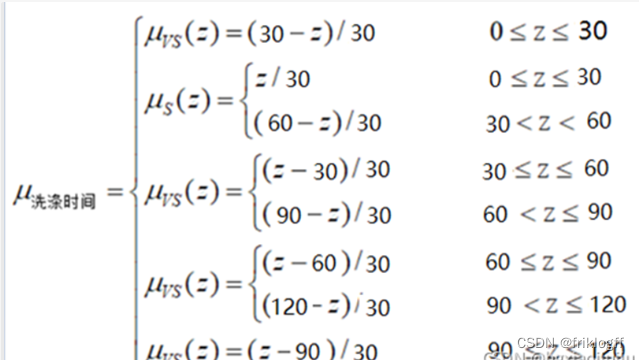
在这里插入图片描述
在这里插入图片描述

import numpy as np
import skfuzzy as fuzz
from skfuzzy import control as ctrl
import matplotlib.pyplot as plt

# 创建输入变量和输出变量
sludge = ctrl.Antecedent(np.arange(0, 101, 1), 'sludge')
grease = ctrl.Antecedent(np.arange(0, 101, 1), 'grease')
washing_time = ctrl.Consequent(np.arange(0, 121, 1), 'washing_time')

# 定义隶属函数
sludge['SD'] = fuzz.trimf(sludge.universe, [0, 0, 50])
sludge['MD'] = fuzz.trimf(sludge.universe, [0, 50, 100])
sludge['LD'] = fuzz.trimf(sludge.universe, [50, 100, 100])

grease['NG'] = fuzz.trimf(grease.universe, [0, 0, 50])
grease['MG'] = fuzz.trimf(grease.universe, [0, 50, 100])
grease['LG'] = fuzz.trimf(grease.universe, [50, 100, 100])

washing_time['VS'] = fuzz.trimf(washing_time.universe, [0, 0, 30])
washing_time['S'] = fuzz.trimf(washing_time.universe, [0, 30, 60])
washing_time['M'] = fuzz.trimf(washing_time.universe, [30, 60, 90])
washing_time['L'] = fuzz.trimf(washing_time.universe, [60, 90, 120])
washing_time['VL'] = fuzz.trimf(washing_time.universe, [90, 120, 120])

# 定义模糊控制规则
rule1 = ctrl.Rule(sludge['SD'] & grease['NG'], washing_time['VS'])
rule2 = ctrl.Rule(sludge['SD'] & grease['MG'], washing_time['M'])
rule3 = ctrl.Rule(sludge['SD'] & grease['LG'], washing_time['L'])
rule4 = ctrl.Rule(sludge['MD'] & grease['NG'], washing_time['S'])
rule5 = ctrl.Rule(sludge['MD'] & grease['MG'], washing_time['M'])
rule6 = ctrl.Rule(sludge['MD'] & grease['LG'], washing_time['L'])
rule7 = ctrl.Rule(sludge['LD'] & grease['MG'], washing_time['M'])
rule8 = ctrl.Rule(sludge['LD'] & grease['LG'], washing_time['L'])
rule9 = ctrl.Rule(sludge['LD'] & grease['LG'], washing_time['VL'])

# 创建控制系统
washing_ctrl = ctrl.ControlSystem([rule1, rule2, rule3, rule4, rule5, rule6, rule7, rule8, rule9])

washing = ctrl.ControlSystemSimulation(washing_ctrl)

# 输入污泥和油脂值
washing.input['sludge'] = 70
washing.input['grease'] = 60

# 进行模糊推理
washing.compute()

# 获取洗涤时间的输出
washing_time.view(sim=washing)

# 打印输出洗涤时间
print("洗涤时间:", washing.output['washing_time'])

# 绘制隶属度函数
sludge.view()
grease.view()
washing_time.view()
plt.show()

4. 模糊控制规则表

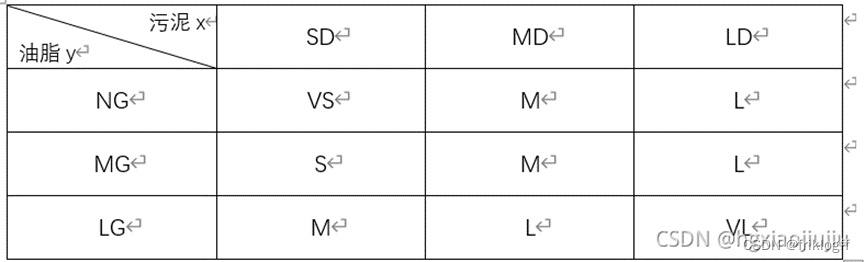
在这里插入图片描述

注：SD（污泥少）、MD（污泥中）、LD（污泥多）、NG（油脂少）、MG（油脂中）、LG（油脂多）、VS（洗涤时间很短）、S（洗涤时间短）、M（洗涤时间中等）、L（洗涤时间长）、VL（洗涤时间很长）。

推论结果立体图
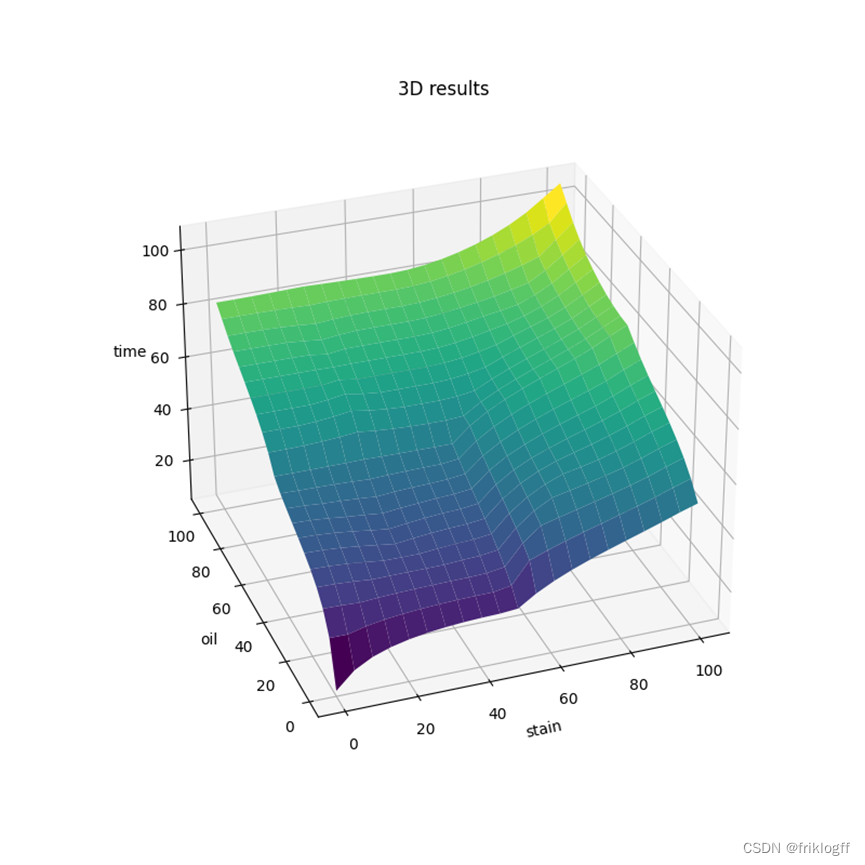
在这里插入图片描述

import numpy as np
import skfuzzy as fuzz
import matplotlib
matplotlib.use('TkAgg')
import matplotlib.pyplot as plt
from skfuzzy import control as ctrl

#定义输入输出的取值范围
#  污泥和油脂范围为[0，100]
#  洗涤时间范围为[0，120]
x_stain = np.arange(0, 101, 1)
x_oil = np.arange(0, 101, 1)
x_time = np.arange(0, 121, 1)
# 定义模糊控制变量
stain = ctrl.Antecedent(x_stain, 'stain')
oil = ctrl.Antecedent(x_oil, 'oil')
time = ctrl.Consequent(x_time, 'time')
# 生成模糊隶属函数
#函数中的三元变量，第一个代表折线的起点，第二是最大值，第三是终点
stain['SD'] = fuzz.trimf(x_stain, [0, 0, 50])  #定义污渍的三角隶属度函数横坐标
stain['MD'] = fuzz.trimf(x_stain, [0, 50, 100])
stain['LD'] = fuzz.trimf(x_stain, [50, 100, 100])
oil['NG'] = fuzz.trimf(x_oil, [0, 0, 50]) #定义油污的三角隶属度函数横坐标
oil['MG'] = fuzz.trimf(x_oil, [0, 50, 100])
oil['LG'] = fuzz.trimf(x_oil, [50, 100, 100])
time['VS'] = fuzz.trimf(x_time, [0, 0, 20]) #定义洗涤时间的三角隶属度函数横坐标
time['S'] = fuzz.trimf(x_time, [0, 20, 50])
time['M'] = fuzz.trimf(x_time, [20, 50, 80])
time['L'] = fuzz.trimf(x_time, [50, 80, 120])
time['VL'] = fuzz.trimf(x_time, [80, 120, 120])

#采用解模糊方法——质心解模糊方式
time.defuzzify_method='centroid'

#规则
rule1=ctrl.Rule(antecedent=((stain['SD'] & oil['NG'])),consequent=time['VS'],label='time=VS')
rule2=ctrl.Rule(antecedent=((stain['SD'] & oil['MG'])|(stain['MD'] & oil['MG'])|(stain['LD'] & oil['NG'])),consequent=time['M'],label='time=M')
rule3=ctrl.Rule(antecedent=((stain['SD'] & oil['LG'])|(stain['MD'] & oil['LG'])|(stain['LD'] & oil['MG'])),consequent=time['L'],label='time=L')
rule4=ctrl.Rule(antecedent=((stain['MD'] & oil['NG'])),consequent=time['S'],label='time=S')
rule5=ctrl.Rule(antecedent=((stain['LD'] & oil['LG'])),consequent=time['VL'],label='time=VL')

# 系统和运行环境初始化
rule=[rule1, rule2, rule3,rule4,rule5]
time_ctrl = ctrl.ControlSystem(rule)
wash_time = ctrl.ControlSystemSimulation(time_ctrl)
#规则中带一些奇怪的规则，处理后输出
for i in range(len(rule)):
    print("rule",i,end=":")
    for item in str(rule[i]):
        if(item!='\n'):
            print(item,end="")
        else:
            break
    print('\t')
#画图
stain.view()
oil.view()
time.view()
#time.view()
plt.show()
#绘制3D图
upsampled=np.linspace(0,101,21)#步距参数
x,y=np.meshgrid(upsampled,upsampled)
z=np.zeros_like(x)
pp=[]
for i in range(0,21):
    for j in range(0,21):
        wash_time.input['stain']=x[i,j]
        wash_time.input['oil']=y[i,j]
        wash_time.compute()
        z[i,j]=wash_time.output['time']
        pp.append(z[i,j])
print('max：',max(pp))
print('min：',min(pp))
from mpl_toolkits.mplot3d import Axes3D
fig=plt.figure(figsize=(8,8))#画布大小
ax=fig.add_subplot(111,projection='3d')
surf=ax.plot_surface(x,y,z,rstride=1,cstride=1,cmap='viridis',linewidth=0.1,antialiased=True)
ax.view_init(30,250)#观察角度
plt.title('3D results')
ax.set_xlabel('stain')
ax.set_ylabel('oil')
ax.set_zlabel('time')
plt.show()

(2)假定当前传感器测得的信息为x0(污泥)=60，y0(油脂)=70，采用模糊决策，给出模糊推理结果，并观察模糊推理的动态仿真环境，给出其动态仿真环境图。

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation

# 导入NumPy库用于数学运算
import numpy as np

# 在Sludge函数和Grease函数中添加输入值检查
def Sludge(a):
    sludge = [0, 0, 0]  # 默认隶属度为0，依次对应SD, MD, LD
    if a < 0:
        a = 0
    elif a > 100:
        a = 100
    if 0 <= a <= 50:
        sludge[0] = (50 - a) / 50
        sludge[1] = a / 50
    elif 50 < a <= 100:
        sludge[1] = (100 - a) / 50
        sludge[2] = (a - 50) / 50
    return sludge

def Grease(a):
    grease = [0, 0, 0]  # 默认隶属度为0,依次对应NG, MG, LG
    if a < 0:
        a = 0
    elif a > 100:
        a = 100
    if 0 <= a <= 50:
        grease[0] = (50 - a) / 50
        grease[1] = a / 50
    elif 50 < a <= 100:
        grease[1] = (100 - a) / 50
        grease[2] = (a - 50) / 50
    return grease


# 3. 规则前提推理，并运算取最小值
def Rules(a, b):  # a为污泥隶属度，b为油脂隶属度
    rules_value = [0, 0, 0, 0, 0, 0, 0, 0, 0]  # 依次对应9条规则结果VS, M, L, S, M, L, M, L, VL
    if a[0] != 0 and b[0] != 0:
        rules_value[0] = min(a[0], b[0])
    if a[0] != 0 and b[1] != 0:
        rules_value[1] = min(a[0], b[1])
    if a[0] != 0 and b[2] != 0:
        rules_value[2] = min(a[0], b[2])
    if a[1] != 0 and b[0] != 0:
        rules_value[3] = min(a[1], b[0])
    if a[1] != 0 and b[1] != 0:
        rules_value[4] = min(a[1], b[1])
    if a[1] != 0 and b[2] != 0:
        rules_value[5] = min(a[1], b[2])
    if a[2] != 0 and b[0] != 0:
        rules_value[6] = min(a[2], b[0])
    if a[2] != 0 and b[1] != 0:
        rules_value[7] = min(a[2], b[1])
    if a[2] != 0 and b[2] != 0:
        rules_value[8] = min(a[2], b[2])
    return rules_value


# 创建一个时间步骤列表
time_steps = np.arange(0, 100, 1)

# 存储模糊输出值的列表
output_values = []

# 创建一个初始传感器输入
x0 = 60  # 初始污泥值
y0 = 70  # 初始油脂值

# 模拟模糊推理过程
for t in time_steps:
    # 模拟传感器测得的信息，可以根据需要在此处引入噪声
    x = x0
    y = y0

    # 计算污泥和油脂的隶属度
    sludge_membership = Sludge(x)
    grease_membership = Grease(y)

    # 规则前提推理
    rule_results = Rules(sludge_membership, grease_membership)

    # 模糊系统总的输出，取各条规则推理结果的最小值
    final_output = max(rule_results)

    # 存储输出值
    output_values.append(final_output)

    # 更新传感器输入（这里示例中的输入简单地增加）
    x0 += 1
    y0 += 1

# 创建图形窗口
fig, ax = plt.subplots()

# 设置初始图形
line, = ax.plot([], [])
ax.set_xlim(0, len(time_steps))
ax.set_ylim(0, 1)
ax.set_xlabel("Time Step")
ax.set_ylabel("Fuzzy Output")
ax.set_title("Fuzzy Logic Control Simulation")


# 更新函数
def update(frame):
    line.set_data(time_steps[:frame + 1], output_values[:frame + 1])
    return line,


# 创建动画
ani = FuncAnimation(fig, update, frames=len(time_steps), blit=True, repeat=False)
plt.show()

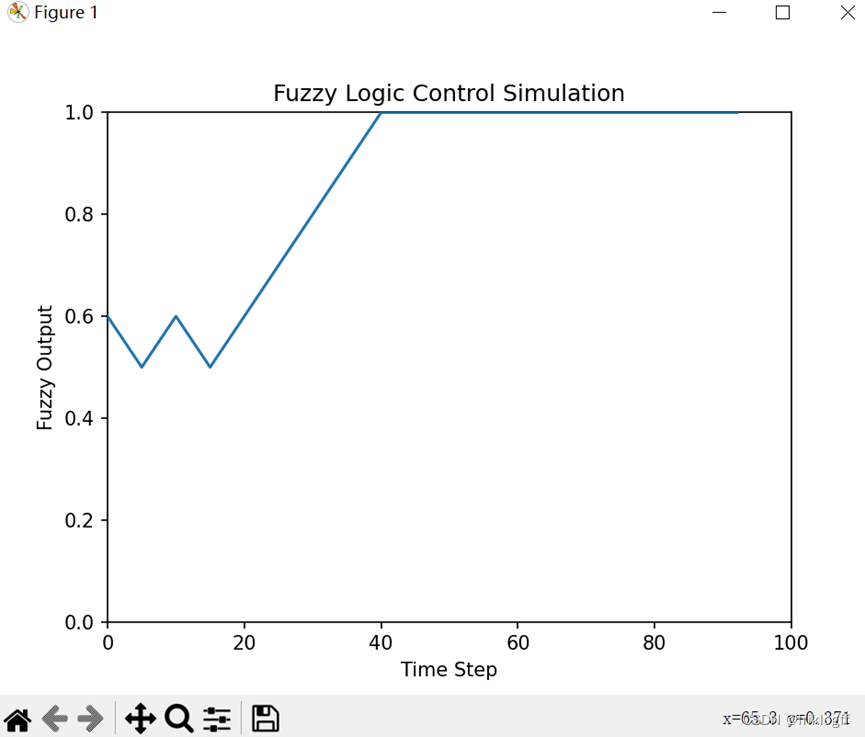
在这里插入图片描述

5.模糊匹配

（1） 模糊匹配
将x=60,y=70带入的隶属度函数中：

（2）规则触发。被触发的规则有4条：

Rule1:IF x is MD AND y is MG THEN z is M;
Rule2:IF x is MD AND y is LG THEN z is L;
Rule3:IF x is LD AND y is MG THEN z is L;
Rule4:IF x is LD AND y is LG THEN z is VL。

（3）规则前提推理。在同一条规则内，前提之间通过交运算得到规则结论。

（4）模糊系统总的输出（聚合）,取各条规则推理结果的并。

（5）去模糊化。采用加权平均判决发的方法。根据洗涤时间隶属函数的反函数用相应的隶属度求出时间论域中对应的值。

# 1. 污泥隶属度计算
def Sludge(a):
    sludge = [0, 0, 0]  # 默认隶属度为0，依次对应SD,MD,LD
    if a < 0 or a > 100:
        return (print("输入值有误"))
    elif 0 <= a <= 50:
        sludge[0] = (50 - a) / 50
        sludge[1] = a / 50
    elif 50 < a <= 100:
        sludge[1] = (100 - a) / 50    #  40/50
        sludge[2] = (a - 50) / 50      # 10/50
    return sludge

# 2. 油脂隶属度计算
def Grease(a):
    grease = [0, 0, 0]  # 默认隶属度为0,依次对应NG,MG,LG
    if a < 0 or a > 100:
        return (print("输入值有误"))
    elif 0 <= a <= 50:
        grease[0] = (50 - a) / 50
        grease[1] = a / 50
    elif 50 < a <= 100:
        grease[1] = (100 - a) / 50   #  30/50
        grease[2] = (a - 50) / 50   #  10/50
    return grease

# 3. 规则前提推理，并运算取最小值
def Rules(a, b):  # a为污泥隶属度，b为油脂隶属度
    rules_value = [0, 0, 0, 0, 0, 0, 0, 0, 0]  # 依次对应9条规则结果VS,M,L,S,M,L,M,L,VL
    if a[0] != 0 and b[0] != 0:
        rules_value[0] = min(a[0], b[0])  # 返回规则下最小值
    if a[0] != 0 and b[1] != 0:
        rules_value[1] = min(a[0], b[1])
    if a[0] != 0 and b[2] != 0:
        rules_value[2] = min(a[0], b[2])
    if a[1] != 0 and b[0] != 0:
        rules_value[3] = min(a[1], b[0])
    if a[1] != 0 and b[1] != 0:
        rules_value[4] = min(a[1], b[1])
    if a[1] != 0 and b[2] != 0:
        rules_value[5] = min(a[1], b[2])
    if a[2] != 0 and b[0] != 0:
        rules_value[6] = min(a[2], b[0])
    if a[2] != 0 and b[1] != 0:
        rules_value[7] = min(a[2], b[1])
    if a[2] != 0 and b[2] != 0:
        rules_value[8] = min(a[2], b[2])
    return rules_value

# 4. 每条规则推理输出
def Inference(a):  # a为9条规则下的结果隶属度
    time_level = [0, 0, 0, 0, 0]  # 默认时间隶属值为0，依次对应VS,S,M,L,VL
    time_level[0] = a[0]    # 0
    time_level[1] = a[3]    # 0
    if (a[1] != 0 or a[4] != 0 or a[6] != 0):  # 去零值然后取剩下的最小值
        list_1 = [a[1], a[4], a[6]]
        for i in range(len(list_1) - 1, -1, -1):
            if list_1[i] == 0:
                list_1.remove(0)
        time_level[2] = min(list_1)
    if (a[2] != 0 or a[5] != 0 or a[7] != 0):
        list_2 = [a[2], a[5], a[7]]
        for i in range(len(list_2) - 1, -1, -1):
            if list_2[i] == 0:
                list_2.remove(0)
        time_level[3] = min(list_2)
    time_level[4] = a[8]
    return time_level

# 5. 由加权平均判决法可得，根据洗涤时间隶属函数的反函数用相应的隶属度求出时间论域中对应的值
def Max_membership(a):  # a为时间隶属度
    time = [0, 0, 0, 0, 0, 0, 0, 0]  # 时间隶属函数八个区间分别对应的时间值
    time[0] = 30 - 30 * a[0]
    time[1] = 30 * a[1]
    time[2] = 60 - 30 * a[1]
    time[3] = 30 * a[2] + 30
    time[4] = 90 - 30 * a[2]
    time[5] = 30 * a[3] + 60
    time[6] = 120 - 30 * a[3]
    time[7] = 30 * a[4] + 90
    sum_1 = time[0] * a[0] + time[1] * a[1] + time[2] * a[1] + time[3] * a[2] + time[4] * a[2] + time[5] * a[3] + time[
        6] * a[3] + time[7] * a[4]
    sum_2 = a[0] + 2 * a[1] + 2 * a[2] + 2 * a[3] + a[4]
    result = sum_1 / sum_2
    return result

# 洗涤时间隶属度函数
def WashTime(a):  # a为时间值
    if 0 <= a <= 30:
        u1 = (30 - a) / 30
        u2 = a / 30
        if (u1 > u2):
            time_level = 'VS'
        else:
            time_level = 'S'
    if 30 < a <= 60:
        u3 = (60 - a) / 30
        u4 = (a - 30) / 30
        if (u3 > u4):
            time_level = 'S'
        else:
            time_level = 'M'
    if 60 < a <= 90:
        u5 = (90 - a) / 30
        u6 = (a - 60) / 30
        if (u5 > u6):
            time_level = 'M'
        else:
            time_level = 'L'
    if 90 < a <= 120:
        u7 = (120 - a) / 30
        u8 = (a - 90) / 30
        if (u7 > u8):
            time_level = 'L'
        else:
            time_level = 'VL'
    return time_level

if __name__ == '__main__':
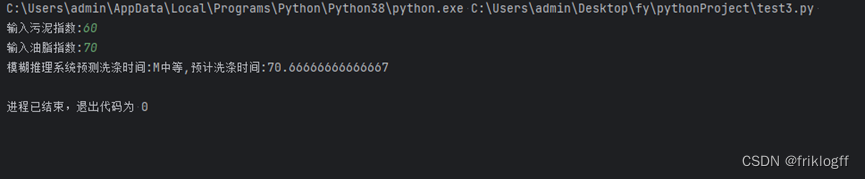
    sludge = int(input("输入污泥指数:"))
    grease = int(input("输入油脂指数:"))
    rules_value = Rules(Sludge(sludge), Grease(grease))
    time_level = Inference(rules_value)  # 时间隶属度
    time_pre = Max_membership(time_level)  # 加权平均判决发求预测时间
    time_sign = WashTime(time_pre)  # 根据预测时间来计算洗涤时间符号
    flag = {'VS': '很短', 'S': '短', 'M': '中等', 'L': '长', 'VL': '很长'}
    print("模糊推理系统预测洗涤时间:{}{},预计洗涤时间:{}".format(time_sign,flag[time_sign], time_pre))

在这里插入图片描述

实验内容及总结

  1. 按照实验要求，给出相应结果。
  2. 分析隶属度、模糊关系和模糊规则的相互关系。

实验思考及实践

理解模糊逻辑原理：模糊逻辑是一种处理模糊信息和不确定性的有效方法。在这个实验中，你需要理解模糊逻辑的原理，包括模糊隶属度、模糊规则以及模糊推理的基本概念。

模糊隶属度函数的设计：在实验中，你需要设计污泥、油脂和洗涤时间的隶属度函数。这需要一定的创造力和理解，以确保隶属度函数可以正确地映射输入值到模糊集合。

模糊规则的构建：根据已知的人类操作经验，你需要构建模糊规则。这包括定义哪些条件下应该触发哪些规则，以及规则的前提和结论是如何关联的。

模糊推理系统的设计：你需要设计一个模糊推理系统，以根据输入的污泥和油脂指数来推断洗衣机的洗涤时间。这包括模糊匹配、规则触发、规则前提推理、模糊系统输出和去模糊化等步骤。

模糊推理结果的解释：在实验中，你将获得模糊推理的结果，包括洗涤时间的隶属度和具体时间值。了解如何解释和应用这些结果对于模糊控制非常重要。

动态仿真环境的观察：根据传感器测得的污泥和油脂指数，你需要观察模糊推理的动态仿真环境。这有助于理解模糊推理系统在不同输入条件下的表现。

模糊推理系统基础知识

1. 简介

模糊推理系统是一种基于模糊逻辑的计算机程序，用于处理模糊信息和进行模糊推理。与传统的布尔逻辑系统相比，模糊推理系统能够处理模糊的、不确定的或部分真实的信息。

模糊推理系统基于模糊逻辑，它引入了模糊集合和模糊关系的概念，以便更好地处理不确定性和模糊性。在模糊推理系统中，命题的真假不再是严格的二元取值，而是一个连续的范围，通常用一个介于0和1之间的实数表示。

2. 模糊逻辑与布尔逻辑的对比

传统的布尔逻辑只有两个取值，即真和假，而模糊逻辑可以处理更为复杂的情况。模糊逻辑允许命题的真假是一个连续的范围，这更符合真实世界中的不确定性和模糊性。

模糊逻辑与布尔逻辑的不同之处在于，模糊逻辑使用模糊集合来表示模糊概念和模糊关系，而布尔逻辑使用精确的集合和关系。

3. 模糊推理系统的基本组成

模糊推理系统由以下几个主要组成部分构成：

模糊规则库

模糊规则库是模糊推理系统的核心组件。它包含一系列模糊规则，每个规则描述了输入变量和输出变量之间的关系。模糊规则通常采用"IF-THEN"的形式，其中IF部分是输入变量的条件，THEN部分是输出变量的结论。

模糊推理引擎

模糊推理引擎是模糊推理系统的计算核心。它根据模糊规则库和输入数据进行推理，并生成模糊结果。推理引擎通常包括模糊化、规则匹配、推理和去模糊化等步骤。

模糊化和去模糊化

在模糊推理系统中，模糊化将现实世界的模糊输入转换为模糊集合。模糊化过程使用隶属函数来描述变量的隶属度，表示变量对某个模糊集合的归属程度。

去模糊化是将模糊结果转换为精确的输出。去模糊化通过使用去模糊函数来确定最终结果的精确值。

4. 模糊推理系统的应用领域

模糊推理系统在许多领域中有广泛的应用，特别是在以下领域：

模糊控制系统

模糊控制系统使用模糊推理系统来处理模糊输入和模糊输出，实现对模糊系统的控制。它在工程领域中广泛应用于控制系统设计，特别是在模糊控制器中。

模糊决策系统

模糊决策系统使用模糊推理系统来处理模糊输入和模糊输出，帮助进行管理和决策支持。它可以不确定性和模糊性为基础，帮助决策者进行决策分析和决策制定。

模糊识别系统

模糊识别系统使用模糊推理系统来处理模糊输入和模糊输出，用于模式识别和数据挖掘。它可以应用于图像识别、语音识别、模式分类等领域。

5. 模糊推理系统的优缺点

模糊推理系统具有以下优点：

  • 能够处理模糊和不确定信息，更贴近真实世界的情况。
  • 具备适应性和鲁棒性，能够应对输入数据的变化和噪声干扰。
  • 可以通过模糊规则库的扩展和调整进行灵活性的调整。

然而，模糊推理系统也存在一些局限性和挑战：

  • 计算复杂性较高，特别是在规则库规模较大时。
  • 不同领域的模糊概念和关系的建模存在主观性和模糊性。
  • 模糊结果的解释和理解可能存在困难。

6. 模糊推理系统的发展趋势

模糊推理系统的研究和应用正不断发展和演进。未来的发展趋势包括但不限于：

  • 结合模糊推理系统与其他人工智能技术，如神经网络和遗传算法，以提高系统性能和效果。
  • 开发更高效的推理算法和优化方法，以应对计算复杂性的挑战。
  • 模糊推理系统在自动化和智能化领域的深入应用，如自动驾驶、智能机器人等。

模糊推理系统作为一种处理模糊信息的有效工具，在各个领域中发挥着重要作用，持续不断地推动着科学研究和技术进步。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1317080.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

DDD挤水分和强行加异性为好友-UMLChina建模知识竞赛第4赛季第25轮

DDD挤水分和强行加异性为好友-UMLChina建模知识竞赛第4赛季第25轮

DDD领域驱动设计批评文集 做强化自测题获得“软件方法建模师”称号 《软件方法》各章合集 参考潘加宇在《软件方法》和UMLChina公众号文章中发表的内容作答。在本文下留言回答。 只要最先答对前3题&#xff0c;即可获得本轮优胜。第4题为附加题&#xff0c;对错不影响优胜者…
阅读更多...
C++ Qt开发：标准Dialog对话框组件

C++ Qt开发：标准Dialog对话框组件

Qt 是一个跨平台C图形界面开发库&#xff0c;利用Qt可以快速开发跨平台窗体应用程序&#xff0c;在Qt中我们可以通过拖拽的方式将不同组件放到指定的位置&#xff0c;实现图形化开发极大的方便了开发效率&#xff0c;本章将重点介绍标准对话框QInputDialog、QFileDialog 这两种…
阅读更多...
阿里云RDS提示过期释放实例了怎么找到库表

阿里云RDS提示过期释放实例了怎么找到库表

做朋友&#xff0c;不需要资格&#xff01;——《全职猎人》 直截了当 一步到位 ~
阅读更多...
Flink系列之：窗口函数Windowing table-valued functions (Windowing TVFs)

Flink系列之：窗口函数Windowing table-valued functions (Windowing TVFs)

Flink系列之&#xff1a;窗口函数Windowing table-valued functions Windowing TVFs 一、窗口函数二、Tumble Windows三、Hop Windows四、Cumulate Windows四、Window Offset 适用流、批 Windows 是处理无限流的核心。 Windows 将流分割成有限大小的“桶”&#xff0c;我们可以…
阅读更多...
Android动画（二）——补间动画

Android动画（二）——补间动画

目录 介绍 Xml文件定义View动画 补充 alpha_animation.xml&#xff08;透明度&#xff09; rotate_animation.xml&#xff08;旋转&#xff09; scale_animation.xml&#xff08;伸缩&#xff09; translate_animation.xml &#xff08;平移&#xff09; group_animation.…
阅读更多...
STM32迪文屏图标控件保姆级教程

STM32迪文屏图标控件保姆级教程

要主图的去末尾&#xff0c;末尾福利图在等着你~~~ 文章目录 前言 开发环境 二、使用步骤 1.添加图标控件 2.设置图标属性 3.图标库ICL文件生成 4.单片机程序编写 容易踩得坑 一、前言 本篇文章主要介绍了在DGBUS平台上使用图标变量的步骤。首先需要在DGBUS中添加一个图标变量控…
阅读更多...
项目抛异常:‘Date‘ 不是可以识别的 内置函数名称。 关键字 ‘AS‘ 附近有语法错误。

项目抛异常:‘Date‘ 不是可以识别的 内置函数名称。 关键字 ‘AS‘ 附近有语法错误。

今天在解决公司C#项目bug问题&#xff0c;顺便记录一下问题及解决方案。入库日报表和出库日报表执行查询失败&#xff1a; ‘DATE’ 不是可以识别的 内置函数名称。 问题截图如下&#xff1a; 这个错误信息看起来是由于在执行远程方法 SIE.WMS.Statistics.StatisticsControll…
阅读更多...
Windows 10如何关闭系统自动更新（实用教程）

Windows 10如何关闭系统自动更新（实用教程）

本章教程&#xff0c;用最简洁的方式介绍在windows10中如何关闭系统自动更新。 目录 一、关闭自动更新服务 二、关闭自动更新组策略 一、关闭自动更新服务 1、 winr 2、services.msc 3、找到并双击 Windows Update 修改启动类型为禁用 二、关闭自动更新组策略 1、winr 2、gp…
阅读更多...
【算法Hot100系列】最长回文子串

【算法Hot100系列】最长回文子串

&#x1f49d;&#x1f49d;&#x1f49d;欢迎来到我的博客&#xff0c;很高兴能够在这里和您见面&#xff01;希望您在这里可以感受到一份轻松愉快的氛围&#xff0c;不仅可以获得有趣的内容和知识&#xff0c;也可以畅所欲言、分享您的想法和见解。 推荐:kwan 的首页,持续学…
阅读更多...
前端已死，网安当立。

前端已死，网安当立。

随着人工智能和低代码的崛起&#xff0c;“前端已死”的声音逐渐兴起。前端已死&#xff1f;尊嘟假嘟&#xff1f;快来发表你的看法吧&#xff01; 此为内容创作模板&#xff0c;在发布之前请将不必要的内容删除 一、为什么会出现“前端已死”的言论 “前端已死”的言论通常…
阅读更多...
结构体基础全家桶（1）创建与初始化

结构体基础全家桶（1）创建与初始化

目录 结构体概念&#xff1a; 结构体类型&#xff1a; 结构体变量的创建&#xff1a; 定义结构体变量的三种方式&#xff1a; 结构体变量的引用&#xff1a; 结构体变量的初始化: 结构体数组&#xff1a; 结构体数组定义&#xff1a; 结构体数组初始化&#xff1a; 结…
阅读更多...
MySQL中的时间函数整理汇总

MySQL中的时间函数整理汇总

1.获取当前时间 -- 获取当前时间 SELECT NOW(); -- 获取当前日期 SELECT CURDATE(); -- 获取当前时分秒 SELECT CURTIME(); 2.获取对应日期对应的年/月/日/月份名/星期数 -- 返回对应日期对应的年/月/日/月份名/星期数 select year(now())as 年,month(now())as 月,day(now())…
阅读更多...
Java Wait Notify

Java Wait Notify

概念 所有对象继承Object方法 用于同步资源锁控制等待以及唤醒 Demo&#xff1a; Message 类同步资源 Waiter 持有Msg&#xff0c;New两个线程Waiter等待 Notifier 持有Msg&#xff0c;通过Msg通知Waiter线程继续 实战 package com.example.demo.java.base.wait;/*** messa…
阅读更多...
LeetCode-克服链表不能随机访问的问题

LeetCode-克服链表不能随机访问的问题

1.重排链表 题目描述&#xff1a; 给定一个单链表 L 的头节点 head &#xff0c;单链表 L 表示为&#xff1a; L0 → L1 → … → Ln - 1 → Ln 请将其重新排列后变为&#xff1a; L0 → Ln → L1 → Ln - 1 → L2 → Ln - 2 → … 不能只是单纯的改变节点内部的值&#xff0…
阅读更多...
node 版本管理(windows/linux)

node 版本管理(windows/linux)

windows 下载 Releases coreybutler/nvm-windows GitHub 查看版本 nvm --version 查看已经安装的版本 nvm ls 安装指定版本 nvm install 5.8.0 卸载制定的版本 nvm uninstall 5.8.0 切换使用指定的版本 nvm use 14.21.3 linux 下载 https://github.com/nvm-sh/nvm/t…
阅读更多...
Azure Machine Learning - 提示工程简介

Azure Machine Learning - 提示工程简介

OpenAI的GPT-3、GPT-3.5和GPT-4模型基于用户输入的文本提示工作。有效的提示构造是使用这些模型的关键技能&#xff0c;涉及到配置模型权重以执行特定任务。这不仅是技术操作&#xff0c;更像是一种艺术&#xff0c;需要经验和直觉。本文旨在介绍适用于所有GPT模型的提示概念和…
阅读更多...
IP代理如何影响网站的速度？代理ip服务器有哪些作用？

IP代理如何影响网站的速度？代理ip服务器有哪些作用？

目录 前言 一、如何影响速度 二、代理服务器的作用 1. 隐藏真实IP地址 2. 绕过访问限制 3. 分布式访问 4. 数据缓存和加速 总结 前言 IP代理是一种通过在用户和目标网站之间引入代理服务器来访问目标网站的方式。代理服务器充当中间人&#xff0c;将用户的请求转发给目…
阅读更多...
基于Hadoop的农产品价格信息检测分析系统

基于Hadoop的农产品价格信息检测分析系统

基于Hadoop的农产品价格信息检测分析系统 前言数据处理模块1. 数据爬取2. 数据清洗与处理3. 数据存储 数据分析与检测模块1. 农产品价格趋势分析2. 农产品价格检索3. 不同市场价格对比 创新点 前言 为了更好地了解农产品市场价格趋势和不同市场之间的价格差异&#xff0c;我设…
阅读更多...
JavaOOP篇----第一篇

JavaOOP篇----第一篇

系列文章目录 文章目录 系列文章目录前言一、什么是B/S架构&#xff1f;什么是C/S架构二、Java都有那些开发平台&#xff1f;三、什么是JDK&#xff1f;什么是JRE?四、Java语言有哪些特点五、面向对象和面向过程的区别 前言 前些天发现了一个巨牛的人工智能学习网站&#xff…
阅读更多...
科大讯飞（深圳）测开面试真题

科大讯飞（深圳）测开面试真题

一面&#xff08;测试组长面&#xff09; 1、上家公司项目以及团队的规模是怎么样的&#xff1f; 2、你负责的项目整体的流程是怎么样的&#xff1f; 3、自动化实施过程中&#xff0c;是如何和业务测试进行沟通的&#xff1f; 4、在上家公司你已经是专职做自动化了&#xf…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023