【图的应用一：最小生成树】- 用 C 语言实现普里姆算法

news2024/9/20 16:50:56

目录

一、最小生成树 

二、普里姆算法的构造过程

三、普里姆算法的实现

 

一、最小生成树 

假设要在 n 个城市之间建立通信联络网，则连通 n 个城市只需要 n - 1 条线路。这时，自然会考虑这样一个问题，如何在最节省经费的前提下建立这个通信网。

在每两个城市之间都可设置一条线路，相应地都要付出一定的经济代价。n 个城市之间，最多可能设置 ​ C_n^2 = \dfrac{n(n - 1)}{2} 条线路，那么如何在这些可能的线路中选择 n - 1 条，以使总的耗费最少呢？

可以用连通网来表示 n 个城市，以及 n 个城市间可能设置的通信路线，其中网的顶点表示城市，边表示两城市之间的线路，赋予边的权值表示相应的代价。对于 n 个顶点的连通网可以建立许多不同的生成树，每一颗生成树都可以是一个通信网，最合理的通信网应该是各边代价之和最小的那颗生成树，称为连通网的最小代价生成树（Minimum Cost Spanning Tree），简称最小生成树。

构造最小生成树有多种算法，其中多数算法利用了最小生成树的下列一种简称为 MST 的性质：

假设 N = (V, E) 是一个连通网，U 是顶点集 V 的一个非空真子集。若 (u, v) 是 N 中所有的一个顶点在 U（u \in U​）中，另一个顶点在 V - U（​v \in V - U）中的边里，具有最小权值的一条边，则必存在一棵包含边 (u, v) 的最小生成树。

可以用反证法来证明：

假设网 N 的任何一棵最小生成树都不包含边 (u, v)，T 是连通网上的一棵最小生成树，由生成树的定义可知，T 中必存在一条从 u 到 v 的路径 P，且在 P 上必存在一条边 (u', v')，其中 u' \in U, v' \in V - U​。

当将边 (u, v) 加入到 T 中时，(u, v) 和 P 构成了一条回路，删去 (u', v') 便可消除回路，同时得到另一颗生成树 T‘。因为 (u, v) 的权值不高于 (u', v')，所以 T' 的权值亦不高于 T，那么 T’ 是包含 (u, v) 的一棵最小生成树，和假设矛盾。

普里姆（Prim）算法和克鲁斯卡尔（Kruskal）算法是两个利用 MST 性质构造最小生成树的算法。

二、普里姆算法的构造过程

假设 N = (V, E) 是连通网，TE 是 N 上最小生成树中边的集合。

  1. U = \{u_0\}(u_0 \in V), TE = \{\}​。

  2. 在所有 ​u \in U, v \in V - U 的边 (u, v) \in E 中找一条权值最小的边 (u_0, v_0) 并入集合 TE，同时 ​v_0 并入 U。

  3. 重复 2，直至 U = V 为止。

此时 TE 中必有 n - 1 条边，则 T = (V, TE) 为 N 的最小生成树。

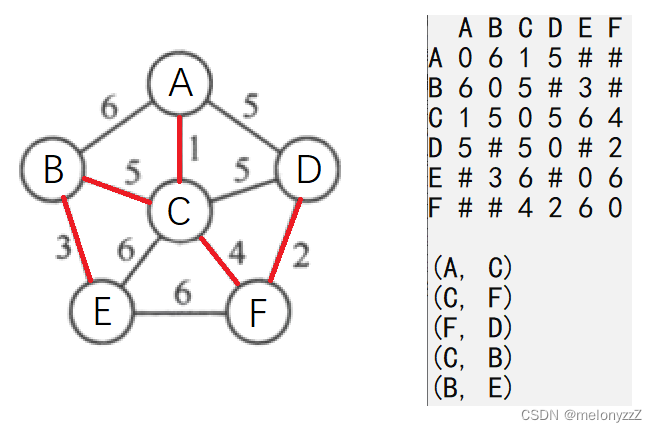
下图所示为一个连通网 G5 从 v1 开始构造最小生成树的例子。可以看出，普里姆算法逐步增加 U 中的顶点，可称为 "加点法"。

每次选择最小边时，可能存在多条同样权值的边可选，此时任选其一即可。

三、普里姆算法的实现

假设无向网 N 以邻接矩阵形式存储，从顶点 u 出发构造 N 的最小生成树 T，要求输出 T 的各条边。

为实现这个算法附设了两个辅助数组 lowcostArr 和 adjVexPosArr。对每个顶点 ，lowcostArr[i - 1] = Min{ cost​ }，即表示 N 中所有的一个顶点在 U 中，另一个顶点是 vi 的边里，最小边上的权值；adjVexPosArr[i - 1] 则表示那条最小边在 U 中的那个顶点在图中的位置。

AMGraph.h：

#pragma once
​
// 无向网
typedef char VertexType;
typedef int EdgeType;
​
#define DEFAULT_CAPACITY 2
​
typedef struct AMGraph
{
    VertexType* vertices;
    EdgeType** edges;
    int vSize;
    int eSize;
    int capacity;
}AMGraph;
​
// 基本操作
void AMGraphInit(AMGraph* pg);
​
void ShowAdjMatrix(AMGraph* pg);
​
int GetVertexPos(AMGraph* pg, VertexType v);
​
void InsertVertex(AMGraph* pg, VertexType v);
void InsertEdge(AMGraph* pg, VertexType v1, VertexType v2, EdgeType cost);
​
// 普里姆算法
void MiniSpanTree_Prim(AMGraph* pg, VertexType u);

AMGraph.c：

#include "AMGraph.h"
#include <assert.h>
#include <stdlib.h>
#include <stdio.h>
​
void AMGraphInit(AMGraph* pg)
{
    assert(pg);
    pg->vSize = pg->eSize = 0;
    pg->capacity = DEFAULT_CAPACITY;
    
    pg->vertices = (VertexType*)malloc(sizeof(VertexType) * pg->capacity);
    assert(pg->vertices);
​
    pg->edges = (EdgeType**)malloc(sizeof(EdgeType*) * pg->capacity);
    assert(pg->edges);
    for (int i = 0; i < pg->capacity; ++i)
    {
        pg->edges[i] = (EdgeType*)malloc(sizeof(EdgeType) * pg->capacity);
        assert(pg->edges[i]);
        for (int j = 0; j < pg->capacity; ++j)
        {
            if (i == j)
                  pg->edges[i][j] = 0;
            else
                  pg->edges[i][j] = INT_MAX;
        }
    }
}
​
void ShowAdjMatrix(AMGraph* pg)
{
    assert(pg);
    printf("  ");
    for (int i = 0; i < pg->vSize; ++i)
    {
        printf("%c ", pg->vertices[i]);
    }
    printf("\n");
​
    for (int i = 0; i < pg->vSize; ++i)
    {
        printf("%c ", pg->vertices[i]);
        for (int j = 0; j < pg->vSize; ++j)
        {
            if (pg->edges[i][j] == INT_MAX)
                printf("# ");  // 用 # 代替 ∞
            else
                printf("%d ", pg->edges[i][j]);
        }
        printf("\n");
    }
}
​
int GetVertexPos(AMGraph* pg, VertexType v)
{
    assert(pg);
    for (int i = 0; i < pg->vSize; ++i)
    {
        if (pg->vertices[i] == v)
            return i;
    }
    return -1;
}
​
void InsertVertex(AMGraph* pg, VertexType v)
{
    assert(pg);
    // 考虑是否需要扩容
    if (pg->vSize == pg->capacity)
    {
        VertexType* tmp1 = (VertexType*)realloc(pg->vertices, sizeof(VertexType) * 2 * pg->capacity);
        assert(tmp1);
        pg->vertices = tmp1;
​
        EdgeType** tmp2 = (EdgeType**)realloc(pg->edges, sizeof(EdgeType*) * 2 * pg->capacity);
        assert(tmp2);
        pg->edges = tmp2;
        for (int i = 0; i < pg->capacity; ++i)
        {
            EdgeType* tmp3 = (EdgeType*)realloc(pg->edges[i], sizeof(EdgeType) * 2 * pg->capacity);
            assert(tmp3);
            pg->edges[i] = tmp3;
            for (int j = pg->capacity; j < 2 * pg->capacity; ++j)
            {
                pg->edges[i][j] = INT_MAX;  
            }
        }
        for (int i = pg->capacity; i < 2 * pg->capacity; ++i)
        {
            pg->edges[i] = (EdgeType*)malloc(sizeof(EdgeType) * 2 * pg->capacity);
            assert(pg->edges[i]);
            for (int j = 0; j < 2 * pg->capacity; ++j)
            {
                if (i == j)
                    pg->edges[i][j] = 0;
                else
                    pg->edges[i][j] = INT_MAX;
            }
        }
​
        pg->capacity *= 2;
    }
    // 插入顶点
    pg->vertices[pg->vSize++] = v;
}
​
void InsertEdge(AMGraph* pg, VertexType v1, VertexType v2, EdgeType cost)
{
    assert(pg);
    int pos1 = GetVertexPos(pg, v1);
    int pos2 = GetVertexPos(pg, v2);
    if (pos1 == -1 || pos2 == -1)
        return;
​
    if (pg->edges[pos1][pos2] != INT_MAX)
        return;
​
    pg->edges[pos1][pos2] = pg->edges[pos2][pos1] = cost;
    ++pg->eSize;
}
​
// 普里姆算法的实现
void MiniSpanTree_Prim(AMGraph* pg, VertexType u)
{
    assert(pg);
    EdgeType* lowcostArr = (EdgeType*)malloc(sizeof(EdgeType) * pg->vSize);
    int* adjVexPosArr = (int*)malloc(sizeof(int) * pg->vSize);
    assert(lowcostArr && adjVexPosArr);
​
    int pos = GetVertexPos(pg, u);
    if (pos == -1)
        return;
    
    for (int i = 0; i < pg->vSize; ++i)
    {
        if (i != pos)
        {
            lowcostArr[i] = pg->edges[pos][i];
            adjVexPosArr[i] = pos;
        }
        else
        {
            lowcostArr[i] = 0;  // 初始，U = {u}
        }
    }
    
    // 选择其余 pg->vSize - 1 个顶点，生成 pg->vSize - 1 条边
    for (int i = 0; i < pg->vSize - 1; ++i)
    {
        EdgeType min = INT_MAX;
        int minIndex = -1;
        for (int j = 0; j < pg->vSize; ++j)
        {
            if (lowcostArr[j] != 0 && lowcostArr[j] < min)
            {
                min = lowcostArr[j];
                minIndex = j;
            }
        }
        printf("(%c, %c)\n", pg->vertices[adjVexPosArr[minIndex]], pg->vertices[minIndex]);
        lowcostArr[minIndex] = 0;  // 将顶点并入 U 
​
        for (int j = 0; j < pg->vSize; ++j)
        {
            if (pg->edges[minIndex][j] < lowcostArr[j])
            {
                lowcostArr[j] = pg->edges[minIndex][j];
                adjVexPosArr[j] = minIndex;
            }
        }
    }
    
    free(lowcostArr);
    free(adjVexPosArr);
}

Test.c：

#include "AMGraph.h"
#include <stdio.h>
​
int main()
{
    AMGraph g;
    AMGraphInit(&g);
    InsertVertex(&g, 'A');
    InsertVertex(&g, 'B');
    InsertVertex(&g, 'C');
    InsertVertex(&g, 'D');
    InsertVertex(&g, 'E');
    InsertVertex(&g, 'F');
    InsertEdge(&g, 'A', 'B', 6);
    InsertEdge(&g, 'A', 'C', 1);
    InsertEdge(&g, 'A', 'D', 5);
    InsertEdge(&g, 'B', 'C', 5);
    InsertEdge(&g, 'B', 'E', 3);
    InsertEdge(&g, 'C', 'D', 5);
    InsertEdge(&g, 'C', 'E', 6);
    InsertEdge(&g, 'C', 'F', 4);
    InsertEdge(&g, 'D', 'F', 2);
    InsertEdge(&g, 'E', 'F', 6);
    ShowAdjMatrix(&g);
    printf("\n");
​
    MiniSpanTree_Prim(&g, 'A');
    return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1316885.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

云仓酒庄的品牌雷盛红酒分享红酒里加二氧化硫有害吗？

云仓酒庄的品牌雷盛红酒分享红酒里加二氧化硫有害吗？

雷盛葡萄酒是广州万豪酒业有限公司旗下主力葡萄酒品牌&#xff0c;该品牌由云仓酒庄负责全国运营。雷盛&#xff08;LEESON&#xff09;品牌系列葡萄酒有幸邀请著名导演张纪中先生担任品牌代言人。采用多国家采购、多葡萄酒品种、多价位区间的全系列整体品牌形式&#xff0c;让…
阅读更多...
谷达冠楠科技：抖音网店到底怎么做靠谱

谷达冠楠科技：抖音网店到底怎么做靠谱

随着互联网的发展&#xff0c;越来越多的人开始尝试在网上开设自己的店铺。而在众多的电商平台中&#xff0c;抖音网店无疑是近年来最受年轻人欢迎的一种方式。那么&#xff0c;抖音网店到底怎么做才能靠谱呢? 首先&#xff0c;我们需要明确一点&#xff0c;无论是在哪个平台上…
阅读更多...
JS对象笔记

JS对象笔记

对象声明 对象也只是一种数据类型/字面值。写对象这个字面值有两种写法&#xff0c;一种是普通的对象&#xff0c;这种对象用new 构造函数&#xff08;&#xff09;&#xff0c;另一种是JS内特有的json对象。这个对象是直接{}就代表对象。且也是在堆内。 对象的构成 无论是上…
阅读更多...
Pytorch当中的.detach()操作是什么意思

Pytorch当中的.detach()操作是什么意思

.detach() 是 PyTorch 中用于从计算图中分离张量的方法。当我们在PyTorch中进行张量运算时&#xff0c;操作会构建一个计算图来跟踪计算历史&#xff0c;这个计算图用于自动求导和反向传播来计算梯度。 使用.detach()方法可以将一个张量从当前的计算图中分离出来&#xff0c;使…
阅读更多...
System作为系统进程陔如何关闭？

System作为系统进程陔如何关闭？

一、简介 system进程是不可以关闭的&#xff0c;它是用来运行一些系统命令的&#xff0c;比如reboot、shutdown等&#xff0c;以及用来运行一些后台程序&#xff0c;比如ntfs-3g、v4l2loopback等。system进程也被用于运行一些内核模块&#xff0c;比如nvidia、atd等。system进程…
阅读更多...
太阳能电池特性测试用太阳光模拟器24H光源

太阳能电池特性测试用太阳光模拟器24H光源

概述 太阳能模拟器是一种在室内模拟太阳光的设备&#xff0c;能够较为准确地模拟太阳辐射的准直性、均匀性和光谱特性。它的基本原理是利用人工光源模拟太阳光辐射&#xff0c;以克服太阳光辐射受环境、时间和气候等因素影响&#xff0c;并且总辐照度不能调节等缺点&#xff0c…
阅读更多...
c++ websocket 协议分析与实现

c++ websocket 协议分析与实现

前言 网上有很多第三方库&#xff0c;nopoll,uwebsockets,libwebsockets,都喜欢回调或太复杂&#xff0c;个人只需要在后端用&#xff0c;所以手动写个&#xff1b; 1:环境 ubuntu18 g(支持c11即可) 第三方库:jsoncpp,openssl 2:安装 jsoncpp 读取json 配置文件 用 自动安装 网…
阅读更多...
【Redis】远程访问配置教程与远程客户端连接测试

【Redis】远程访问配置教程与远程客户端连接测试

前言 Redis 是一种基于内存的高性能键值存储数据库&#xff0c;常用于缓存、会话管理和实时数据分析等场景。在默认情况下&#xff0c;Redis 不允许远程连接&#xff0c;为了进行远程连接&#xff0c;需要进行一些配置和操作。接下来将介绍如何修改配置文件以允许远程连接&…
阅读更多...
毅速：3D打印随形水路 提高良品率和生产效率的新利器

毅速：3D打印随形水路 提高良品率和生产效率的新利器

随着科技的不断发展&#xff0c;3D打印技术已经成为模具制造领域的一种重要技术。其中&#xff0c;模具随形水路的设计和制造是提高注塑产品良品率和生产效率的关键环节。 模具随形水路是一种根据产品形状设计的水路&#xff0c;可以更靠近产品&#xff0c;并在模具内热点集中区…
阅读更多...
SpringBoot 源码解析2：启动流程1

SpringBoot 源码解析2：启动流程1

SpringBoot 源码解析2&#xff1a;启动流程1 1.启动方式2.SpringBootApplication3.SpringApplication3.1 构造器SpringApplication3.2 SpringApplication#run 3.3 SpringApplication#run 中关键方法3.1 SpringApplication#prepareEnvironment3.2 SpringApplication#prepareCont…
阅读更多...
前端登录界面网站设计模板--HTML+CSS

前端登录界面网站设计模板--HTML+CSS

🎀登录表单 💖效果展示 💖HTML代码展示 <!DOCTYPE html> <html lang="en" > <head></
阅读更多...
【机器学习】044_Kaggle房价预测（机器学习模型实战）

【机器学习】044_Kaggle房价预测（机器学习模型实战）

参考自《动手学深度学习》中“Kaggle比赛实战&#xff1a;预测房价”一节 一、数据准备 首先从网站上下载要获取的房价数据。 DATA_HUB是一个字典&#xff0c;用来将数据集名称的字符串和数据集相关的二元组一一对应。 二元组包含两个值&#xff1a;数据集的URL和用来验证文…
阅读更多...
网站转换APP源代码 WebAPP源代码 网站生成APP源代码 Flutter项目 带控制端

网站转换APP源代码 WebAPP源代码 网站生成APP源代码 Flutter项目 带控制端

源码介绍 一款网站转换成APP的源代码,开发语言使用Flutter,开发工具使用的是AndroidStudio,你只需要在APP源代码里面填写你的域名,即可生成即可生成APP,包括安卓或者苹果,与此同时我们提供了APP的控制端.你可以通过控制端设置APP的颜色、添加APP的图标、添加APP的菜单栏目。 …
阅读更多...
2020 ICPC·小米邀请赛 决赛 J. Rikka with Book(状压dp)

2020 ICPC·小米邀请赛 决赛 J. Rikka with Book(状压dp)

题目 登录—专业IT笔试面试备考平台_牛客网 n(n<20)本书&#xff0c;放在桌子上&#xff0c; 第i本书的可以看成是li(li<1e3)*1*1的物体&#xff0c;其中长为li&#xff0c;宽为1&#xff0c;高为1&#xff0c; 质量均匀分布&#xff0c;且为wi(wi<1e3) 求n本书摞…
阅读更多...
配置测试MQtt

配置测试MQtt

连接测试
阅读更多...
【数据结构】使用循环链表结构实现约瑟夫环问题

【数据结构】使用循环链表结构实现约瑟夫环问题

目录 1.循环链表的定义 2.约瑟夫环问题 3.创建循环链表 4.删除节点操作 5.打印所有节点 6.实现约瑟夫环问题的完整程序代码 &#x1f308;嗨&#xff01;我是Filotimo__&#x1f308;。很高兴与大家相识&#xff0c;希望我的博客能对你有所帮助。 &#x1f4a1;本文由Filotimo_…
阅读更多...
基于Java SSM框架实现智能停车场系统项目【项目源码+论文说明】

基于Java SSM框架实现智能停车场系统项目【项目源码+论文说明】

基于java的SSM框架实现智能停车场系统演示 摘要 本论文主要论述了如何使用JAVA语言开发一个智能停车场管理系统&#xff0c;本系统将严格按照软件开发流程进行各个阶段的工作&#xff0c;采用B/S架构&#xff0c;面向对象编程思想进行项目开发。在引言中&#xff0c;作者将论述…
阅读更多...
MySQL数据库的基础概念

MySQL数据库的基础概念

目录 顾名思义&#xff0c;数据库是用于存储数据的&#xff0c;那这些数据被存储在哪呢&#xff1f; 文件也能存储数据&#xff0c;那在这个基础上&#xff0c;为什么还要搞出一个数据库来存储数据呢&#xff1f; MySQL的客户端登录/退出指令、服务端的启动/关闭指令 数据…
阅读更多...
oracle怎么导入dmp文件？？？？？？

oracle怎么导入dmp文件？？？？？？

目录 oracle怎么导入dmp文件&#xff1f;&#xff1f;&#xff1f;&#xff1f;&#xff1f;&#xff1f; 先看&#xff1a; 方法一&#xff1a;【推荐】 winR输入 输入&#xff1a; 检验&#xff1a; 导入成功&#xff01; 方法二&#xff1a; 直接在 PLSQL Developer…
阅读更多...
技术探秘：在RISC Zero中验证FHE——由隐藏到证明：FHE验证的ZK路径（1）

技术探秘：在RISC Zero中验证FHE——由隐藏到证明：FHE验证的ZK路径（1）

1. 引言 开源代码实现见&#xff1a; https://github.com/hashcloak/fhe_risc0_zkvm&#xff08;Rust&#xff09;https://github.com/weikengchen/vfhe-profiled&#xff08;Rust&#xff09;https://github.com/l2iterative/vfhe0&#xff08;Rust&#xff09; L2IV Resea…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023