文章目录
- 解析几何
- 2023
- 真题(2023-07)-几何-解析几何-最值-画图求最值-两线相减求最大-联想三角形的“两边差小于第三边”,当为第三边为最大
- 真题(2023-19)-几何-解析几何-最值-画图求最值-圆方程画出圆的形状-两点间距离型最值=动点在多边形上运动求最值:求 ( x − a ) 2 + ( y − b ) 2 (x-a)^2+(y-b)^2 (x−a)2+(y−b)2最值:设 ( x − a ) 2 + ( y − b ) 2 = r 2 (x-a)^2+(y-b)^2=r^2 (x−a)2+(y−b)2=r2,此时,要求的式子可看作是圆的半径的平方。由于 d = ( x − a ) 2 + ( y − b ) 2 d=\sqrt{(x-a)^2+(y-b)^2} d=(x−a)2+(y−b)2,故所求式子 ( x − a ) 2 + ( y − b ) 2 (x-a)^2+(y-b)^2 (x−a)2+(y−b)2可转化为求定点 ( a , b ) (a,b) (a,b)到动点 ( x , y ) (x,y) (x,y)的距离的平方。
- 真题(2023-20)-几何-解析几何-画图求最值-圆方程画出圆的形状-举反例
- 2022
- 2021
- 真题(2021-10)-几何-解析几何-最值-画图求最值-若四边形ABCD的对角线AC、BD满足AC⊥BD,则 S A B C D = 1 2 A C ⋅ B D S_{ABCD}=\frac{1}{2}AC·BD SABCD=21AC⋅BD
- 真题(2021-20)-几何-解析几何-位置-线圆位置-相切-圆求出圆心转为点到直线的距离公式: l : a x + b y + c = 0 l:ax+by+c=0 l:ax+by+c=0,点( x 0 , y 0 x_0,y_0 x0,y0)到 l l l的距离为 d = ∣ a x 0 + b y 0 + c ∣ a 2 + b 2 d=\frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}} d=a2+b2∣ax0+by0+c∣
- 真题(2021-21)-几何-解析几何-位置-线圆位置-相离-也还是转为圆心点到直线的距离公式
- 2020
- 真题(2020-07)-几何-解析几何-最值-画图求最值-圆方程画出圆的形状;-算术-绝对值-绝对值号、一个等号和两个未知数=函数画图;算术-绝对值不等式函数-图像;-前10题可以特值法,设未知数;
- 真题(2020-17)-几何-解析几何-位置-线圆位置-相切-圆心点到直线距离公式 d = ∣ a x 0 + b y 0 + c ∣ a 2 + b 2 d=\frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}} d=a2+b2∣ax0+by0+c∣
- 2019
- 真题(2019-05)-几何-解析几何-对称-点与直线的对称点坐标公式: l : a x + b y + c = 0 l:ax+by+c=0 l:ax+by+c=0,点( x 0 , y 0 x_0,y_0 x0,y0)关于 l l l的对称点的坐标公式: ( x 0 − 2 a a x 0 + b y 0 + c a 2 + b 2 , y 0 − 2 b a x 0 + b y 0 + c a 2 + b 2 ) (x_0-2a\frac{ax_0+by_0+c}{a^2+b^2},y_0-2b\frac{ax_0+by_0+c}{a^2+b^2}) (x0−2aa2+b2ax0+by0+c,y0−2ba2+b2ax0+by0+c)
- 真题(2019-18)-几何-解析几何-位置-相交-线圆相交-圆方程化为标准圆方程求出圆心,求圆心点直线距离公式。
- 真题(2019-24)-几何-解析几何-最值-这一题考试遇到就跳过了。_。-解析几何求最值画图-
- 2018
- 真题(2018-10)-几何-解析几何-位置-线圆位置-相切转为圆心点到直线距离公式 d = ∣ a x 0 + b y 0 + c ∣ a 2 + b 2 d=\frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}} d=a2+b2∣ax0+by0+c∣
- 真题(2018-22)-几何-解析几何-线性规划-先看边界再取整
- 真题(2018-24)--A-几何-解析几何-位置-线圆位置-转换为圆心点到直线距离公式
- 2017
- 真题(2017-17)-A-几何-解析几何-圆的方程
- 2016
- 真题(2016-10)-几何-解析几何-画图-中点坐标公式
- 真题(2016-11)-几何-解析几何-最值-截距型最值-有x,y转为斜截式,根据图像判断最值;-解析几何求最值,需要转为函数,如直线方程,圆方程等画图判断最值。
- 真题(2016-22)-几何-图像的判断
- 2015
- 真题(2015-11)-几何-解析几何-直线与圆的位置关系
- 真题(2015-16)-D-几何-解析几何-直线与圆的位置关系
- 2014
- 2013
解析几何
2023
真题(2023-07)-几何-解析几何-最值-画图求最值-两线相减求最大-联想三角形的“两边差小于第三边”,当为第三边为最大

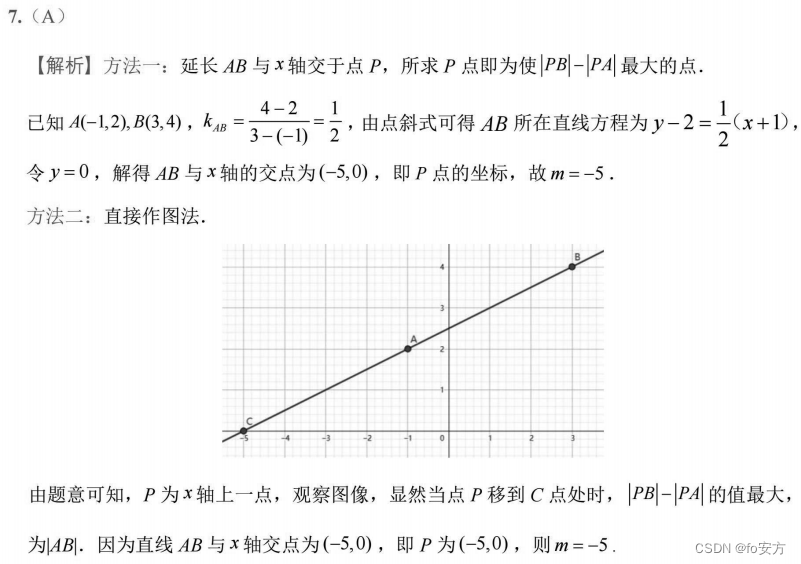
解析几何——最值——汇总
斜率型最值:求
y
−
b
x
−
a
\frac{y-b}{x-a}
x−ay−b最值:设
k
=
y
−
b
x
−
a
k=\frac{y-b}{x-a}
k=x−ay−b,转化为求定点
(
a
,
b
)
(a,b)
(a,b)和动点
(
x
,
y
)
(x,y)
(x,y)相连所成直线的斜率范围。
截距型最值=动点在多边形上运动求最值:求
a
x
±
b
y
ax±by
ax±by最值:设
a
x
±
b
y
=
c
ax±by=c
ax±by=c,即
y
=
−
a
b
x
±
c
b
y=-\frac{a}{b}x±\frac{c}{b}
y=−bax±bc,转化为求动直线截距的最值。或者,边界点处取最值,逐一验证多边形顶点。
两点间距离型最值=动点在多边形上运动求最值:求
(
x
−
a
)
2
+
(
y
−
b
)
2
(x-a)^2+(y-b)^2
(x−a)2+(y−b)2最值:设
(
x
−
a
)
2
+
(
y
−
b
)
2
=
r
2
(x-a)^2+(y-b)^2=r^2
(x−a)2+(y−b)2=r2,此时,要求的式子可看作是圆的半径的平方。由于
d
=
(
x
−
a
)
2
+
(
y
−
b
)
2
d=\sqrt{(x-a)^2+(y-b)^2}
d=(x−a)2+(y−b)2,故所求式子
(
x
−
a
)
2
+
(
y
−
b
)
2
(x-a)^2+(y-b)^2
(x−a)2+(y−b)2可转化为求定点
(
a
,
b
)
(a,b)
(a,b)到动点
(
x
,
y
)
(x,y)
(x,y)的距离的平方。
对称求最值=动点在直线上运动求最值:
①同侧求最小(考查形式:已知
A
、
B
A、B
A、B两点在直线l的同侧,在
l
l
l上找一点
P
P
P,使得
P
A
+
P
B
PA+PB
PA+PB最小;解法:作点A(或点B)关于直线
l
l
l的对称点
A
1
A_1
A1,连接
A
1
B
A_1B
A1B,交直线
l
l
l于点
P
P
P,则
A
1
B
A_1B
A1B即为所求的最小值,有
(
P
A
+
P
B
)
m
i
n
=
A
1
B
(PA+PB)_{min}=A_1B
(PA+PB)min=A1B);
②异侧求最大(考查形式:已知
A
、
B
A、B
A、B两点在直线
l
l
l异侧,在
l
l
l上找一点
P
P
P,使得
P
A
−
P
B
PA-PB
PA−PB最大;解法:作点A(或点B)关于直线
l
l
l的对称点
A
1
A_1
A1,连接
A
1
B
A_1B
A1B,交直线
l
l
l于点
P
P
P,则
A
1
B
A_1B
A1B即为所求的最大值,即
(
P
A
−
P
B
)
m
a
x
=
A
1
B
(PA-PB)_{max}=A_1B
(PA−PB)max=A1B)。——【同侧加和求最小值,异侧相减求最大值】
圆心求最值=动点在圆上运动求最值:
①求圆外或圆内一点A到圆上距离的最值:
m
a
x
=
O
A
+
r
;
m
i
n
=
∣
O
A
−
r
∣
max=OA+r;min=|OA-r|
max=OA+r;min=∣OA−r∣
②直线与圆相离,求圆上点到直线距离的最值:求出圆心到直线的距离d,则距离最大值为
d
+
r
d+r
d+r,最小值为
d
−
r
d-r
d−r;直线与圆相切,最大值为
2
r
2r
2r,最小值为0;直线与圆相交,最大值为
d
+
r
d+r
d+r,最小值为0。
③两圆相离,求两圆上的点的距离的最值:求出圆心距
O
1
O
2
O_1O_2
O1O2,则距离最大值为
O
1
O
2
+
r
1
+
r
2
O_1O_2+r_1+r_2
O1O2+r1+r2,最小值为
O
1
O
2
−
r
1
−
r
2
O_1O_2-r_1-r_2
O1O2−r1−r2。
④过圆内一点最长或最短的弦,最长的弦为过该点的直径;最短的弦是以该点为中点的弦(与最长弦垂直)——【①求圆上的点到直线距离的最值求出圆心到直线的距离,再根据圆与直线的位置关系,求解。一般是距离加半径是最大值,距离减半径是最小值。②求两圆上的点的距离的最值。求出圆心距,再减半径或加半径即可。】
真题(2023-19)-几何-解析几何-最值-画图求最值-圆方程画出圆的形状-两点间距离型最值=动点在多边形上运动求最值:求 ( x − a ) 2 + ( y − b ) 2 (x-a)^2+(y-b)^2 (x−a)2+(y−b)2最值:设 ( x − a ) 2 + ( y − b ) 2 = r 2 (x-a)^2+(y-b)^2=r^2 (x−a)2+(y−b)2=r2,此时,要求的式子可看作是圆的半径的平方。由于 d = ( x − a ) 2 + ( y − b ) 2 d=\sqrt{(x-a)^2+(y-b)^2} d=(x−a)2+(y−b)2,故所求式子 ( x − a ) 2 + ( y − b ) 2 (x-a)^2+(y-b)^2 (x−a)2+(y−b)2可转化为求定点 ( a , b ) (a,b) (a,b)到动点 ( x , y ) (x,y) (x,y)的距离的平方。
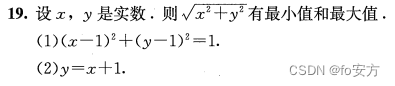

真题(2023-20)-几何-解析几何-画图求最值-圆方程画出圆的形状-举反例
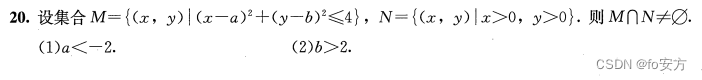

2022
2021
真题(2021-10)-几何-解析几何-最值-画图求最值-若四边形ABCD的对角线AC、BD满足AC⊥BD,则 S A B C D = 1 2 A C ⋅ B D S_{ABCD}=\frac{1}{2}AC·BD SABCD=21AC⋅BD
10.已知ABCD是圆
x
2
+
y
2
=
25
x^2+y^2=25
x2+y2=25的内接四边形,若
A
,
C
A,C
A,C是直线
x
=
3
x =3
x=3与圆
x
2
+
y
2
=
25
x^2+y^2=25
x2+y2=25的交点,则四边形ABCD面积的最大值为( )。
A.20
B.24
C.40
D.48
E.80


真题(2021-20)-几何-解析几何-位置-线圆位置-相切-圆求出圆心转为点到直线的距离公式: l : a x + b y + c = 0 l:ax+by+c=0 l:ax+by+c=0,点( x 0 , y 0 x_0,y_0 x0,y0)到 l l l的距离为 d = ∣ a x 0 + b y 0 + c ∣ a 2 + b 2 d=\frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}} d=a2+b2∣ax0+by0+c∣
20.设a为实数,圆C:
x
2
+
y
2
=
a
x
+
a
y
x^2+y^2=ax+ay
x2+y2=ax+ay,则能确定圆C的方程。
(1)直线
x
+
y
=
1
x +y=1
x+y=1与圆C相切。
(2)直线
x
−
y
=
1
x-y =1
x−y=1与圆C相切。

真题(2021-21)-几何-解析几何-位置-线圆位置-相离-也还是转为圆心点到直线的距离公式
21.设x ,y为实数,则能确定
x
≤
y
x≤y
x≤y。
(1)
x
2
≤
y
−
1
x^2≤y-1
x2≤y−1。
(2)
x
2
+
(
y
−
2
)
2
≤
2
x^2+(y-2)^2≤2
x2+(y−2)2≤2。

2020
真题(2020-07)-几何-解析几何-最值-画图求最值-圆方程画出圆的形状;-算术-绝对值-绝对值号、一个等号和两个未知数=函数画图;算术-绝对值不等式函数-图像;-前10题可以特值法,设未知数;
7、设实数 x, y 满足
∣
x
−
2
∣
+
∣
y
−
2
∣
≤
2
|x-2|+|y-2|≤2
∣x−2∣+∣y−2∣≤2,则
x
2
+
y
2
x^2+y^2
x2+y2的取值范围是( )
A.[2,18]
B.[2, 20]
C.[2, 36]
D.[4,18]
E.[4, 20]


真题(2020-17)-几何-解析几何-位置-线圆位置-相切-圆心点到直线距离公式 d = ∣ a x 0 + b y 0 + c ∣ a 2 + b 2 d=\frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}} d=a2+b2∣ax0+by0+c∣
17、曲线 上的点到
x
2
+
y
2
=
2
x
+
2
y
x^2+y^2=2x+2y
x2+y2=2x+2y上的点到
a
x
+
b
y
+
2
=
0
ax+by+\sqrt2=0
ax+by+2=0的距离最小值大于 1。
(1)
a
2
+
b
2
=
1
a^2+b^2=1
a2+b2=1
(2)
a
>
0
,
b
>
0
a>0,b>0
a>0,b>0


2019
真题(2019-05)-几何-解析几何-对称-点与直线的对称点坐标公式: l : a x + b y + c = 0 l:ax+by+c=0 l:ax+by+c=0,点( x 0 , y 0 x_0,y_0 x0,y0)关于 l l l的对称点的坐标公式: ( x 0 − 2 a a x 0 + b y 0 + c a 2 + b 2 , y 0 − 2 b a x 0 + b y 0 + c a 2 + b 2 ) (x_0-2a\frac{ax_0+by_0+c}{a^2+b^2},y_0-2b\frac{ax_0+by_0+c}{a^2+b^2}) (x0−2aa2+b2ax0+by0+c,y0−2ba2+b2ax0+by0+c)
5、设圆C与圆
(
x
−
5
)
2
+
y
2
=
2
(x-5)^2+y^2=2
(x−5)2+y2=2关于
y
=
2
x
y=2x
y=2x 对称,则圆 C 方程为( )
A.
(
x
−
3
)
2
+
(
y
−
4
)
2
=
2
(x-3)^2+(y-4)^2=2
(x−3)2+(y−4)2=2
B.
(
x
+
4
)
2
+
(
y
−
3
)
2
=
2
(x+4)^2+(y-3)^2=2
(x+4)2+(y−3)2=2
C.
(
x
−
3
)
2
+
(
y
+
4
)
2
=
2
(x-3)^2+(y+4)^2=2
(x−3)2+(y+4)2=2
D.
(
x
+
3
)
2
+
(
y
−
3
)
2
=
2
(x+3)^2+(y-3)^2=2
(x+3)2+(y−3)2=2
E.
(
x
+
3
)
2
+
(
y
−
4
)
2
=
2
(x+3)^2+(y-4)^2=2
(x+3)2+(y−4)2=2
对称问题
圆
(
x
−
5
)
2
+
y
2
=
2
(x-5)^2+y^2=2
(x−5)2+y2=2的圆心为(5,0),关于直线y=2x的对称点设为(x,y),则
{
y
2
=
2
⋅
x
+
5
12
,
y
x
−
5
=
−
1
2
,
\begin{cases} \frac{y}{2}=2·\frac{x+5}{12}, \\ \frac{y}{x-5}=-\frac{1}{2}, \end{cases}
{2y=2⋅12x+5,x−5y=−21,
解得:
{
x
=
−
3
y
=
4
\begin{cases} x=-3 \\ y=4 \end{cases}
{x=−3y=4
所以圆C的方程为
(
x
+
3
)
2
+
(
y
−
4
)
2
=
2
(x+3)^2+(y-4)^2=2
(x+3)2+(y−4)2=2

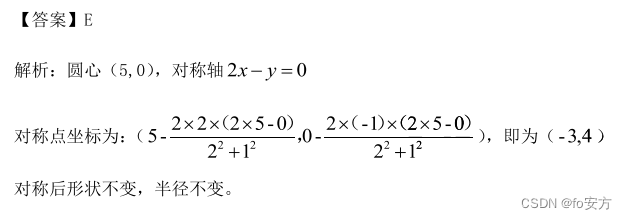
真题(2019-18)-几何-解析几何-位置-相交-线圆相交-圆方程化为标准圆方程求出圆心,求圆心点直线距离公式。
18、直线
y
=
k
x
y =kx
y=kx 与圆
x
2
+
y
2
−
4
x
+
3
=
0
x^{2}+ y^2−4x+3 =0
x2+y2−4x+3=0 有两个交点
(1)
−
3
3
<
k
<
0
-{\sqrt{3}\over3}<k<0
−33<k<0
(2)
0
<
k
<
2
2
0<k<{\sqrt{2}\over2}
0<k<22


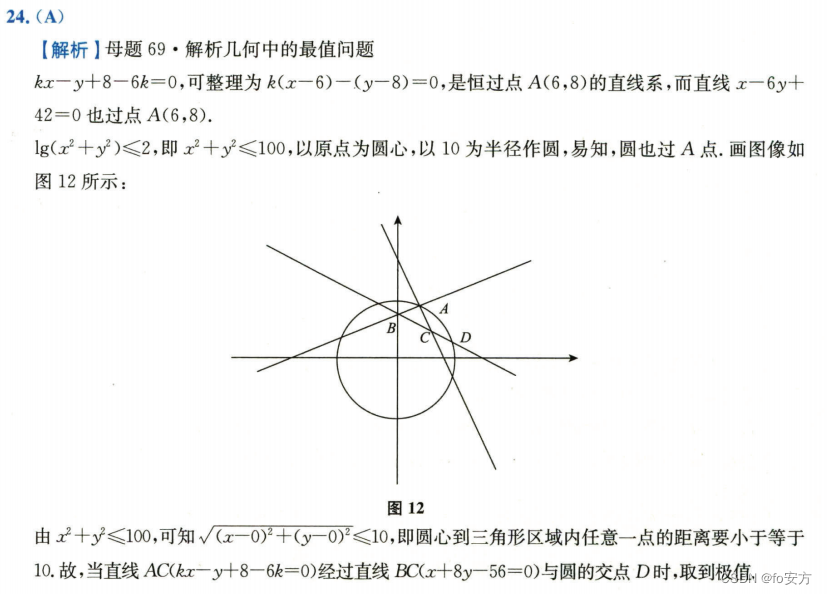
真题(2019-24)-几何-解析几何-最值-这一题考试遇到就跳过了。_。-解析几何求最值画图-
24、设三角区域D由直线 x + 8 y − 56 = 0 , x − 6 y + 42 = 0 x+8y-56=0,x-6y+42=0 x+8y−56=0,x−6y+42=0与 k x − y + 8 − 6 k = 0 ( k < 0 ) kx-y+8-6k=0(k<0) kx−y+8−6k=0(k<0)围成,则对任意的 ( x , y ) (x,y) (x,y), l g ( x 2 + y 2 ) ≤ 2 lg(x^2+y^2)≤2 lg(x2+y2)≤2
(1)
k
∈
(
−
∞
,
−
1
]
k∈(-∞,-1]
k∈(−∞,−1]
(2)
k
∈
[
−
1
,
−
1
8
)
k∈[-1,-{1\over8})
k∈[−1,−81)


2018
真题(2018-10)-几何-解析几何-位置-线圆位置-相切转为圆心点到直线距离公式 d = ∣ a x 0 + b y 0 + c ∣ a 2 + b 2 d=\frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}} d=a2+b2∣ax0+by0+c∣
10.已知圆C :
x
2
+
(
y
−
a
)
2
=
b
x^2+(y-a)^2=b
x2+(y−a)2=b,若圆C 在点(1,2)处的切线与 y 轴交点为(0,3),则ab =( )
A.-2
B.-1
C.0
D.1
E.2




真题(2018-22)-几何-解析几何-线性规划-先看边界再取整
22.已知点
P
(
m
,
0
)
P(m,0)
P(m,0),
A
(
1
,
3
)
A(1,3)
A(1,3),
B
(
2
,
1
)
,
B(2,1),
B(2,1),点
(
x
,
y
)
(x,y)
(x,y)在三角形
P
A
B
PAB
PAB上,则
x
−
y
x- y
x−y的最小值与最大值分别为
−
2
-2
−2和
1
1
1。
(1)
m
≤
1
m ≤ 1
m≤1
(2)
m
≥
−
2
m ≥ -2
m≥−2




解题方法
第一步:根据题目写出限定条件对应的不等式组。
第二步:“先看边界”,将不等式直接取等号,求得未知数的解。
第三步:“再取整数”,若所求解为整数,则此整数解即为方程的解;若所求解为小数,则取其左右相邻的整数。进行验证,求出最值。
【注意】这种方法并不严谨,但对于绝大多数选择题来说可以快速得分。
口诀:线性规划问题:先看边界再取整
真题(2018-24)–A-几何-解析几何-位置-线圆位置-转换为圆心点到直线距离公式
24.设a, b 实数,则圆
x
2
+
y
2
=
2
y
x^2+y^2=2y
x2+y2=2y与直线
x
+
a
y
=
b
x+ay=b
x+ay=b不相交。
(1)
∣
a
−
b
∣
>
1
+
a
2
|a-b|>\sqrt{1+a^2}
∣a−b∣>1+a2
(2)
∣
a
+
b
∣
>
1
+
a
2
|a+b|>\sqrt{1+a^2}
∣a+b∣>1+a2




2017
真题(2017-17)-A-几何-解析几何-圆的方程
17.圆
x
2
+
y
2
−
a
x
−
b
y
+
c
=
0
x^2+y^2-ax-by+c=0
x2+y2−ax−by+c=0与 x 轴相切,则能确定c 的值。
(1)已知a 的值
(2)已知b 的值
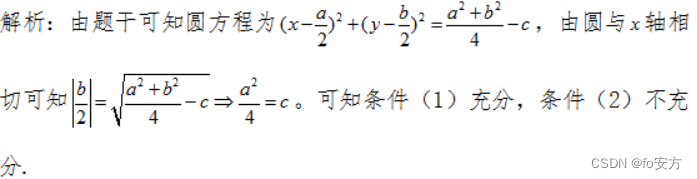

2016
真题(2016-10)-几何-解析几何-画图-中点坐标公式
10.圆
x
2
+
y
2
−
6
x
+
4
y
=
0
x^2+y^2-6x+4y=0
x2+y2−6x+4y=0上到原点距离最远的点是( )
A.(-3,2)
B.(3,-2)
C.(6,4)
D.(-6,4)
E.(6,-4)
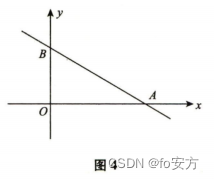
真题(2016-11)-几何-解析几何-最值-截距型最值-有x,y转为斜截式,根据图像判断最值;-解析几何求最值,需要转为函数,如直线方程,圆方程等画图判断最值。
11.如图 4 所示,点 A,B,O 的坐标分别为(4,0)、(0,3)、(0,0),若(x, y) 是△AOB中的点,则
2
x
+
3
y
2x+3y
2x+3y的最大值为( )
A.6
B.7
C.8
D.9
E.12

真题(2016-22)-几何-图像的判断
22.已知M是一个平面有限点集,则平面上存在到M中各点距离相等的点。
(1)M中只有三个点。
(2)M中的任意三点都不共线。

2015
真题(2015-11)-几何-解析几何-直线与圆的位置关系
11.若直线 y = ax 与圆
(
x
−
a
)
2
+
y
2
=
1
(x-a)^2+y^2=1
(x−a)2+y2=1相切,则
a
2
a^2
a2 = ( )
A.
1
+
3
2
\frac{1+\sqrt{3}}{2}
21+3
B.
1
+
3
2
1+\frac{\sqrt{3}}{2}
1+23
C.
5
2
\frac{\sqrt{5}}{2}
25
D.
1
+
5
2
1+\frac{\sqrt{5}}{2}
1+25
E.
1
+
5
2
\frac{1+\sqrt{5}}{2}
21+5


真题(2015-16)-D-几何-解析几何-直线与圆的位置关系
16.圆盘
x
2
+
y
2
≤
2
(
x
+
y
)
x^2+y^2≤2(x+y)
x2+y2≤2(x+y)被直线 L 分成面积相等的两部分。
(1) L:
x
+
y
=
2
x + y = 2
x+y=2
(2) L:
2
x
−
y
=
1
2x-y= 1
2x−y=1


2014
真题(2014-11)-几何-解析几何-圆方程
11.已知直线
l
l
l是圆
x
2
+
y
2
=
5
x^2+y^2=5
x2+y2=5在点(1,2)处的切线,则
l
l
l在 y 轴上的截距为( )
A.
2
5
\frac{2}{5}
52
B.
2
3
\frac{2}{3}
32
C.
3
2
\frac{3}{2}
23
D.
5
2
\frac{5}{2}
25
E.5


真题(2014-25)-A-几何-解析几何-最值-两点间距离型最值=动点在多边形上运动求最值:求 ( x − a ) 2 + ( y − b ) 2 (x-a)^2+(y-b)^2 (x−a)2+(y−b)2最值:设 ( x − a ) 2 + ( y − b ) 2 = r 2 (x-a)^2+(y-b)^2=r^2 (x−a)2+(y−b)2=r2,此时,要求的式子可看作是圆的半径的平方。由于 d = ( x − a ) 2 + ( y − b ) 2 d=\sqrt{(x-a)^2+(y-b)^2} d=(x−a)2+(y−b)2,故所求式子 ( x − a ) 2 + ( y − b ) 2 (x-a)^2+(y-b)^2 (x−a)2+(y−b)2可转化为求定点 ( a , b ) (a,b) (a,b)到动点 ( x , y ) (x,y) (x,y)的距离的平方。
25.已知 x, y 为实数,则
x
2
+
y
2
=
1
x^2+y^2=1
x2+y2=1。
(1)
4
y
−
3
x
≥
5
4y - 3x ≥ 5
4y−3x≥5
(2)
(
x
−
1
)
2
+
(
y
−
1
)
2
≥
5
(x-1)^2+(y-1)^2≥5
(x−1)2+(y−1)2≥5


2013
真题(2013-08)-几何-解析几何-对称-点与直线的对称点坐标公式: l : a x + b y + c = 0 l:ax+by+c=0 l:ax+by+c=0,点( x 0 , y 0 x_0,y_0 x0,y0)关于 l l l的对称点的坐标公式: ( x 0 − 2 a a x 0 + b y 0 + c a 2 + b 2 , y 0 − 2 b a x 0 + b y 0 + c a 2 + b 2 ) (x_0-2a\frac{ax_0+by_0+c}{a^2+b^2},y_0-2b\frac{ax_0+by_0+c}{a^2+b^2}) (x0−2aa2+b2ax0+by0+c,y0−2ba2+b2ax0+by0+c)
8.点
(
0
,
4
)
(0,4)
(0,4)关于直线
2
x
+
y
+
1
=
0
2x+y+1=0
2x+y+1=0的对称点为( )。
A.
(
2
,
0
)
(2,0)
(2,0)
B.
(
−
3
,
0
)
(-3,0)
(−3,0)
C.
(
−
6
,
1
)
(-6,1)
(−6,1)
D.
(
4
,
2
)
(4,2)
(4,2)
E.
(
−
4
,
2
)
(-4,2)
(−4,2)

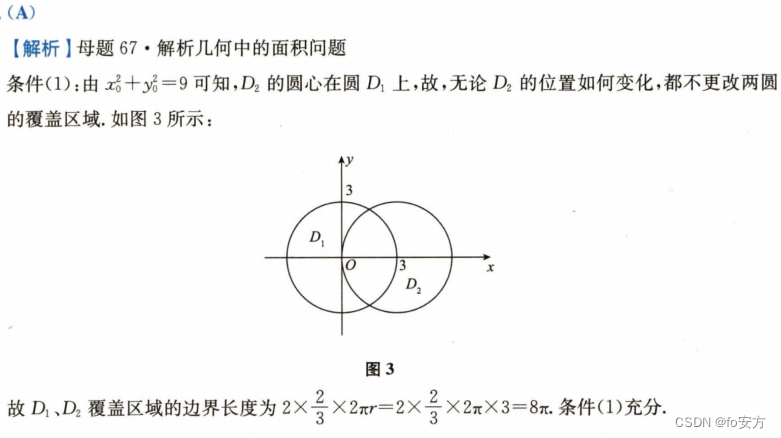
真题(2013-16)-几何-解析几何-面积
16.已知平面区域D1={
(
x
,
y
)
∣
x
2
+
y
2
≤
9
{(x,y)|x^2+y^2≤9}
(x,y)∣x2+y2≤9},D2={
(
x
,
y
)
∣
(
x
−
x
0
)
2
+
(
y
−
y
0
)
2
≤
9
{(x,y)|(x-x_0)^2+(y-y_0)^2≤9}
(x,y)∣(x−x0)2+(y−y0)2≤9},则
D
1
,
D
2
D1,D2
D1,D2覆盖区域的边界长度为
8
π
8π
8π。
(1)
x
0
2
+
y
0
2
=
9
x_0^2+y_0^2=9
x02+y02=9
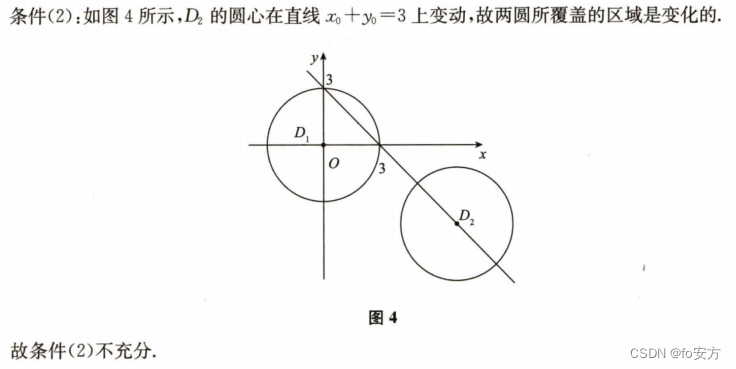
(2)
x
0
+
y
0
=
3
x_0+y_0=3
x0+y0=3