刚体四元数姿态控制 一文中没有证明的公式
R
(
Q
1
)
R
(
Q
2
)
=
R
(
Q
1
∘
Q
2
)
R(Q_1)R(Q_2)=R(Q_1\circ Q_2)
R(Q1)R(Q2)=R(Q1∘Q2)
在这篇文章中证明。
首先找几个数测试是否等价。
quaternions.py的代码见 自用的四元数、欧拉角、旋转矩阵转换代码。
下面的代码中,为了测试准确,四元数还要保证归一化,不如事先拿几个欧拉角转成四元数。
import numpy as np
from pythonsrc.quaternions import *
e1 = np.array([2, 0.2, -0.1])
e2 = np.array([0.1, 0.2, -0.3])
q1 = Euler_To_Quaternion(e1)
q2 = Euler_To_Quaternion(e2)
q3 = Quaternion_Product(q2, q1)
r1 = Quaternion_to_Rotation(q1)
r2 = Quaternion_to_Rotation(q2)
r3 = Quaternion_to_Rotation(q3)
r4 = r1 @ r2
print(sum(sum(r3-r4)))
然后测试一下 sympy 计算四元数转旋转矩阵的公式是否正确。
import sympy
def Antisymmetric(mat):
ans = sympy.Matrix([
[0, -mat[2], mat[1]],
[mat[2], 0, -mat[0]],
[-mat[1], mat[0], 0],
])
return ans
qsa, qvxa, qvya, qvza = sympy.symbols('s_a, v_{ax}, v_{ay}, v_{az}')
qsb, qvxb, qvyb, qvzb = sympy.symbols('s_b, v_{bx}, v_{by}, v_{bz}')
qva = sympy.Matrix([qvxa, qvya, qvza])
qvb = sympy.Matrix([qvxb, qvyb, qvzb])
result = (qsa**2 - qva.T.dot(qva))*sympy.eye(3)
result += 2*qva*qva.T
result += 2*qsa*Antisymmetric(qva)
sympy.print_latex(result)
最后正式验证等价性。
import sympy
def Antisymmetric(mat):
ans = sympy.Matrix([
[0, -mat[2], mat[1]],
[mat[2], 0, -mat[0]],
[-mat[1], mat[0], 0],
])
return ans
def Quaternion_to_Rotation(Q):
q0, q1, q2, q3 = Q
return sympy.Matrix([
[q0*q0+q1*q1-q2*q2-q3*q3, 2*q1*q2-2*q0*q3, 2*q1*q3+2*q0*q2],
[2*q1*q2+2*q0*q3, q0*q0-q1*q1+q2*q2-q3*q3, 2*q2*q3-2*q0*q1],
[2*q1*q3-2*q0*q2, 2*q2*q3+2*q0*q1, q0*q0-q1*q1-q2*q2+q3*q3],
])
def Quaternion_Product(Q1, Q2):
w1, x1, y1, z1 = Q1
w2, x2, y2, z2 = Q2
w = w1 * w2 - x1 * x2 - y1 * y2 - z1 * z2
x = w1 * x2 + x1 * w2 + y1 * z2 - z1 * y2
y = w1 * y2 + y1 * w2 + z1 * x2 - x1 * z2
z = w1 * z2 + z1 * w2 + x1 * y2 - y1 * x2
return sympy.Matrix([w, x, y, z])
qsa, qvxa, qvya, qvza = sympy.symbols('s_a, v_{ax}, v_{ay}, v_{az}')
qsb, qvxb, qvyb, qvzb = sympy.symbols('s_b, v_{bx}, v_{by}, v_{bz}')
Qa = sympy.Matrix([qsa, qvxa, qvya, qvza])
Qb = sympy.Matrix([qsb, qvxb, qvyb, qvzb])
Qc = Quaternion_Product(Qa, Qb)
Ra = Quaternion_to_Rotation(Qa)
Rb = Quaternion_to_Rotation(Qb)
Rc = Quaternion_to_Rotation(Qc)
Rd = Ra @ Rb
sympy.print_latex(Rc)
sympy.print_latex(Rd)
err = Rc - Rd
sympy.print_latex(err.expand())
输出结果如下,公式特别复杂,两个矩阵的误差为0。
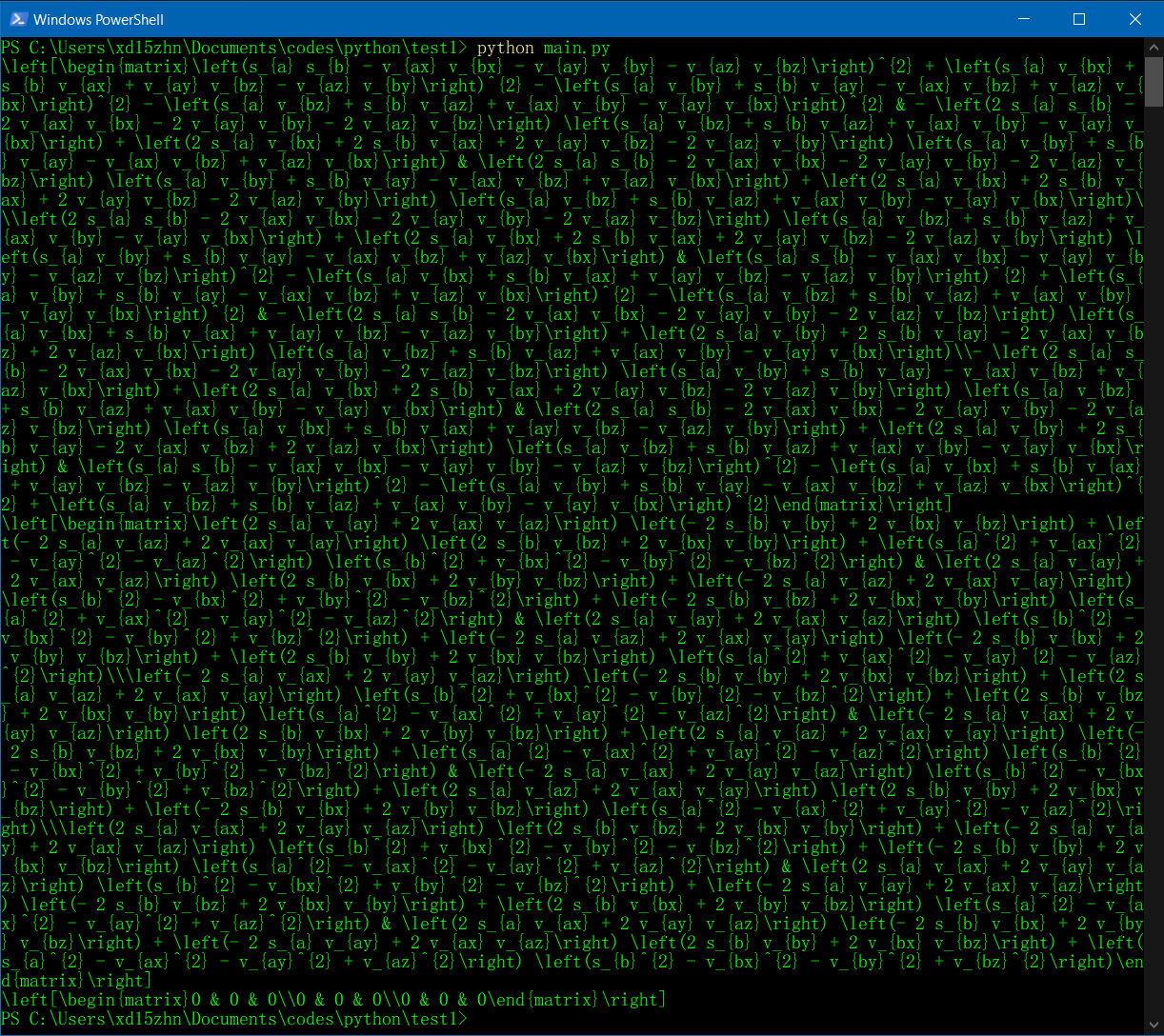
[
(
s
a
s
b
−
v
a
x
v
b
x
−
v
a
y
v
b
y
−
v
a
z
v
b
z
)
2
+
(
s
a
v
b
x
+
s
b
v
a
x
+
v
a
y
v
b
z
−
v
a
z
v
b
y
)
2
−
(
s
a
v
b
y
+
s
b
v
a
y
−
v
a
x
v
b
z
+
v
a
z
v
b
x
)
2
−
(
s
a
v
b
z
+
s
b
v
a
z
+
v
a
x
v
b
y
−
v
a
y
v
b
x
)
2
−
(
2
s
a
s
b
−
2
v
a
x
v
b
x
−
2
v
a
y
v
b
y
−
2
v
a
z
v
b
z
)
(
s
a
v
b
z
+
s
b
v
a
z
+
v
a
x
v
b
y
−
v
a
y
v
b
x
)
+
(
2
s
a
v
b
x
+
2
s
b
v
a
x
+
2
v
a
y
v
b
z
−
2
v
a
z
v
b
y
)
(
s
a
v
b
y
+
s
b
v
a
y
−
v
a
x
v
b
z
+
v
a
z
v
b
x
)
(
2
s
a
s
b
−
2
v
a
x
v
b
x
−
2
v
a
y
v
b
y
−
2
v
a
z
v
b
z
)
(
s
a
v
b
y
+
s
b
v
a
y
−
v
a
x
v
b
z
+
v
a
z
v
b
x
)
+
(
2
s
a
v
b
x
+
2
s
b
v
a
x
+
2
v
a
y
v
b
z
−
2
v
a
z
v
b
y
)
(
s
a
v
b
z
+
s
b
v
a
z
+
v
a
x
v
b
y
−
v
a
y
v
b
x
)
(
2
s
a
s
b
−
2
v
a
x
v
b
x
−
2
v
a
y
v
b
y
−
2
v
a
z
v
b
z
)
(
s
a
v
b
z
+
s
b
v
a
z
+
v
a
x
v
b
y
−
v
a
y
v
b
x
)
+
(
2
s
a
v
b
x
+
2
s
b
v
a
x
+
2
v
a
y
v
b
z
−
2
v
a
z
v
b
y
)
(
s
a
v
b
y
+
s
b
v
a
y
−
v
a
x
v
b
z
+
v
a
z
v
b
x
)
(
s
a
s
b
−
v
a
x
v
b
x
−
v
a
y
v
b
y
−
v
a
z
v
b
z
)
2
−
(
s
a
v
b
x
+
s
b
v
a
x
+
v
a
y
v
b
z
−
v
a
z
v
b
y
)
2
+
(
s
a
v
b
y
+
s
b
v
a
y
−
v
a
x
v
b
z
+
v
a
z
v
b
x
)
2
−
(
s
a
v
b
z
+
s
b
v
a
z
+
v
a
x
v
b
y
−
v
a
y
v
b
x
)
2
−
(
2
s
a
s
b
−
2
v
a
x
v
b
x
−
2
v
a
y
v
b
y
−
2
v
a
z
v
b
z
)
(
s
a
v
b
x
+
s
b
v
a
x
+
v
a
y
v
b
z
−
v
a
z
v
b
y
)
+
(
2
s
a
v
b
y
+
2
s
b
v
a
y
−
2
v
a
x
v
b
z
+
2
v
a
z
v
b
x
)
(
s
a
v
b
z
+
s
b
v
a
z
+
v
a
x
v
b
y
−
v
a
y
v
b
x
)
−
(
2
s
a
s
b
−
2
v
a
x
v
b
x
−
2
v
a
y
v
b
y
−
2
v
a
z
v
b
z
)
(
s
a
v
b
y
+
s
b
v
a
y
−
v
a
x
v
b
z
+
v
a
z
v
b
x
)
+
(
2
s
a
v
b
x
+
2
s
b
v
a
x
+
2
v
a
y
v
b
z
−
2
v
a
z
v
b
y
)
(
s
a
v
b
z
+
s
b
v
a
z
+
v
a
x
v
b
y
−
v
a
y
v
b
x
)
(
2
s
a
s
b
−
2
v
a
x
v
b
x
−
2
v
a
y
v
b
y
−
2
v
a
z
v
b
z
)
(
s
a
v
b
x
+
s
b
v
a
x
+
v
a
y
v
b
z
−
v
a
z
v
b
y
)
+
(
2
s
a
v
b
y
+
2
s
b
v
a
y
−
2
v
a
x
v
b
z
+
2
v
a
z
v
b
x
)
(
s
a
v
b
z
+
s
b
v
a
z
+
v
a
x
v
b
y
−
v
a
y
v
b
x
)
(
s
a
s
b
−
v
a
x
v
b
x
−
v
a
y
v
b
y
−
v
a
z
v
b
z
)
2
−
(
s
a
v
b
x
+
s
b
v
a
x
+
v
a
y
v
b
z
−
v
a
z
v
b
y
)
2
−
(
s
a
v
b
y
+
s
b
v
a
y
−
v
a
x
v
b
z
+
v
a
z
v
b
x
)
2
+
(
s
a
v
b
z
+
s
b
v
a
z
+
v
a
x
v
b
y
−
v
a
y
v
b
x
)
2
]
\left[\begin{matrix}\left(s_{a} s_{b} - v_{ax} v_{bx} - v_{ay} v_{by} - v_{az} v_{bz}\right)^{2} + \left(s_{a} v_{bx} + s_{b} v_{ax} + v_{ay} v_{bz} - v_{az} v_{by}\right)^{2} - \left(s_{a} v_{by} + s_{b} v_{ay} - v_{ax} v_{bz} + v_{az} v_{bx}\right)^{2} - \left(s_{a} v_{bz} + s_{b} v_{az} + v_{ax} v_{by} - v_{ay} v_{bx}\right)^{2} & - \left(2 s_{a} s_{b} - 2 v_{ax} v_{bx} - 2 v_{ay} v_{by} - 2 v_{az} v_{bz}\right) \left(s_{a} v_{bz} + s_{b} v_{az} + v_{ax} v_{by} - v_{ay} v_{bx}\right) + \left(2 s_{a} v_{bx} + 2 s_{b} v_{ax} + 2 v_{ay} v_{bz} - 2 v_{az} v_{by}\right) \left(s_{a} v_{by} + s_{b} v_{ay} - v_{ax} v_{bz} + v_{az} v_{bx}\right) & \left(2 s_{a} s_{b} - 2 v_{ax} v_{bx} - 2 v_{ay} v_{by} - 2 v_{az} v_{bz}\right) \left(s_{a} v_{by} + s_{b} v_{ay} - v_{ax} v_{bz} + v_{az} v_{bx}\right) + \left(2 s_{a} v_{bx} + 2 s_{b} v_{ax} + 2 v_{ay} v_{bz} - 2 v_{az} v_{by}\right) \left(s_{a} v_{bz} + s_{b} v_{az} + v_{ax} v_{by} - v_{ay} v_{bx}\right)\\\left(2 s_{a} s_{b} - 2 v_{ax} v_{bx} - 2 v_{ay} v_{by} - 2 v_{az} v_{bz}\right) \left(s_{a} v_{bz} + s_{b} v_{az} + v_{ax} v_{by} - v_{ay} v_{bx}\right) + \left(2 s_{a} v_{bx} + 2 s_{b} v_{ax} + 2 v_{ay} v_{bz} - 2 v_{az} v_{by}\right) \left(s_{a} v_{by} + s_{b} v_{ay} - v_{ax} v_{bz} + v_{az} v_{bx}\right) & \left(s_{a} s_{b} - v_{ax} v_{bx} - v_{ay} v_{by} - v_{az} v_{bz}\right)^{2} - \left(s_{a} v_{bx} + s_{b} v_{ax} + v_{ay} v_{bz} - v_{az} v_{by}\right)^{2} + \left(s_{a} v_{by} + s_{b} v_{ay} - v_{ax} v_{bz} + v_{az} v_{bx}\right)^{2} - \left(s_{a} v_{bz} + s_{b} v_{az} + v_{ax} v_{by} - v_{ay} v_{bx}\right)^{2} & - \left(2 s_{a} s_{b} - 2 v_{ax} v_{bx} - 2 v_{ay} v_{by} - 2 v_{az} v_{bz}\right) \left(s_{a} v_{bx} + s_{b} v_{ax} + v_{ay} v_{bz} - v_{az} v_{by}\right) + \left(2 s_{a} v_{by} + 2 s_{b} v_{ay} - 2 v_{ax} v_{bz} + 2 v_{az} v_{bx}\right) \left(s_{a} v_{bz} + s_{b} v_{az} + v_{ax} v_{by} - v_{ay} v_{bx}\right)\\- \left(2 s_{a} s_{b} - 2 v_{ax} v_{bx} - 2 v_{ay} v_{by} - 2 v_{az} v_{bz}\right) \left(s_{a} v_{by} + s_{b} v_{ay} - v_{ax} v_{bz} + v_{az} v_{bx}\right) + \left(2 s_{a} v_{bx} + 2 s_{b} v_{ax} + 2 v_{ay} v_{bz} - 2 v_{az} v_{by}\right) \left(s_{a} v_{bz} + s_{b} v_{az} + v_{ax} v_{by} - v_{ay} v_{bx}\right) & \left(2 s_{a} s_{b} - 2 v_{ax} v_{bx} - 2 v_{ay} v_{by} - 2 v_{az} v_{bz}\right) \left(s_{a} v_{bx} + s_{b} v_{ax} + v_{ay} v_{bz} - v_{az} v_{by}\right) + \left(2 s_{a} v_{by} + 2 s_{b} v_{ay} - 2 v_{ax} v_{bz} + 2 v_{az} v_{bx}\right) \left(s_{a} v_{bz} + s_{b} v_{az} + v_{ax} v_{by} - v_{ay} v_{bx}\right) & \left(s_{a} s_{b} - v_{ax} v_{bx} - v_{ay} v_{by} - v_{az} v_{bz}\right)^{2} - \left(s_{a} v_{bx} + s_{b} v_{ax} + v_{ay} v_{bz} - v_{az} v_{by}\right)^{2} - \left(s_{a} v_{by} + s_{b} v_{ay} - v_{ax} v_{bz} + v_{az} v_{bx}\right)^{2} + \left(s_{a} v_{bz} + s_{b} v_{az} + v_{ax} v_{by} - v_{ay} v_{bx}\right)^{2}\end{matrix}\right]
(sasb−vaxvbx−vayvby−vazvbz)2+(savbx+sbvax+vayvbz−vazvby)2−(savby+sbvay−vaxvbz+vazvbx)2−(savbz+sbvaz+vaxvby−vayvbx)2(2sasb−2vaxvbx−2vayvby−2vazvbz)(savbz+sbvaz+vaxvby−vayvbx)+(2savbx+2sbvax+2vayvbz−2vazvby)(savby+sbvay−vaxvbz+vazvbx)−(2sasb−2vaxvbx−2vayvby−2vazvbz)(savby+sbvay−vaxvbz+vazvbx)+(2savbx+2sbvax+2vayvbz−2vazvby)(savbz+sbvaz+vaxvby−vayvbx)−(2sasb−2vaxvbx−2vayvby−2vazvbz)(savbz+sbvaz+vaxvby−vayvbx)+(2savbx+2sbvax+2vayvbz−2vazvby)(savby+sbvay−vaxvbz+vazvbx)(sasb−vaxvbx−vayvby−vazvbz)2−(savbx+sbvax+vayvbz−vazvby)2+(savby+sbvay−vaxvbz+vazvbx)2−(savbz+sbvaz+vaxvby−vayvbx)2(2sasb−2vaxvbx−2vayvby−2vazvbz)(savbx+sbvax+vayvbz−vazvby)+(2savby+2sbvay−2vaxvbz+2vazvbx)(savbz+sbvaz+vaxvby−vayvbx)(2sasb−2vaxvbx−2vayvby−2vazvbz)(savby+sbvay−vaxvbz+vazvbx)+(2savbx+2sbvax+2vayvbz−2vazvby)(savbz+sbvaz+vaxvby−vayvbx)−(2sasb−2vaxvbx−2vayvby−2vazvbz)(savbx+sbvax+vayvbz−vazvby)+(2savby+2sbvay−2vaxvbz+2vazvbx)(savbz+sbvaz+vaxvby−vayvbx)(sasb−vaxvbx−vayvby−vazvbz)2−(savbx+sbvax+vayvbz−vazvby)2−(savby+sbvay−vaxvbz+vazvbx)2+(savbz+sbvaz+vaxvby−vayvbx)2
[
(
2
s
a
v
a
y
+
2
v
a
x
v
a
z
)
(
−
2
s
b
v
b
y
+
2
v
b
x
v
b
z
)
+
(
−
2
s
a
v
a
z
+
2
v
a
x
v
a
y
)
(
2
s
b
v
b
z
+
2
v
b
x
v
b
y
)
+
(
s
a
2
+
v
a
x
2
−
v
a
y
2
−
v
a
z
2
)
(
s
b
2
+
v
b
x
2
−
v
b
y
2
−
v
b
z
2
)
(
2
s
a
v
a
y
+
2
v
a
x
v
a
z
)
(
2
s
b
v
b
x
+
2
v
b
y
v
b
z
)
+
(
−
2
s
a
v
a
z
+
2
v
a
x
v
a
y
)
(
s
b
2
−
v
b
x
2
+
v
b
y
2
−
v
b
z
2
)
+
(
−
2
s
b
v
b
z
+
2
v
b
x
v
b
y
)
(
s
a
2
+
v
a
x
2
−
v
a
y
2
−
v
a
z
2
)
(
2
s
a
v
a
y
+
2
v
a
x
v
a
z
)
(
s
b
2
−
v
b
x
2
−
v
b
y
2
+
v
b
z
2
)
+
(
−
2
s
a
v
a
z
+
2
v
a
x
v
a
y
)
(
−
2
s
b
v
b
x
+
2
v
b
y
v
b
z
)
+
(
2
s
b
v
b
y
+
2
v
b
x
v
b
z
)
(
s
a
2
+
v
a
x
2
−
v
a
y
2
−
v
a
z
2
)
(
−
2
s
a
v
a
x
+
2
v
a
y
v
a
z
)
(
−
2
s
b
v
b
y
+
2
v
b
x
v
b
z
)
+
(
2
s
a
v
a
z
+
2
v
a
x
v
a
y
)
(
s
b
2
+
v
b
x
2
−
v
b
y
2
−
v
b
z
2
)
+
(
2
s
b
v
b
z
+
2
v
b
x
v
b
y
)
(
s
a
2
−
v
a
x
2
+
v
a
y
2
−
v
a
z
2
)
(
−
2
s
a
v
a
x
+
2
v
a
y
v
a
z
)
(
2
s
b
v
b
x
+
2
v
b
y
v
b
z
)
+
(
2
s
a
v
a
z
+
2
v
a
x
v
a
y
)
(
−
2
s
b
v
b
z
+
2
v
b
x
v
b
y
)
+
(
s
a
2
−
v
a
x
2
+
v
a
y
2
−
v
a
z
2
)
(
s
b
2
−
v
b
x
2
+
v
b
y
2
−
v
b
z
2
)
(
−
2
s
a
v
a
x
+
2
v
a
y
v
a
z
)
(
s
b
2
−
v
b
x
2
−
v
b
y
2
+
v
b
z
2
)
+
(
2
s
a
v
a
z
+
2
v
a
x
v
a
y
)
(
2
s
b
v
b
y
+
2
v
b
x
v
b
z
)
+
(
−
2
s
b
v
b
x
+
2
v
b
y
v
b
z
)
(
s
a
2
−
v
a
x
2
+
v
a
y
2
−
v
a
z
2
)
(
2
s
a
v
a
x
+
2
v
a
y
v
a
z
)
(
2
s
b
v
b
z
+
2
v
b
x
v
b
y
)
+
(
−
2
s
a
v
a
y
+
2
v
a
x
v
a
z
)
(
s
b
2
+
v
b
x
2
−
v
b
y
2
−
v
b
z
2
)
+
(
−
2
s
b
v
b
y
+
2
v
b
x
v
b
z
)
(
s
a
2
−
v
a
x
2
−
v
a
y
2
+
v
a
z
2
)
(
2
s
a
v
a
x
+
2
v
a
y
v
a
z
)
(
s
b
2
−
v
b
x
2
+
v
b
y
2
−
v
b
z
2
)
+
(
−
2
s
a
v
a
y
+
2
v
a
x
v
a
z
)
(
−
2
s
b
v
b
z
+
2
v
b
x
v
b
y
)
+
(
2
s
b
v
b
x
+
2
v
b
y
v
b
z
)
(
s
a
2
−
v
a
x
2
−
v
a
y
2
+
v
a
z
2
)
(
2
s
a
v
a
x
+
2
v
a
y
v
a
z
)
(
−
2
s
b
v
b
x
+
2
v
b
y
v
b
z
)
+
(
−
2
s
a
v
a
y
+
2
v
a
x
v
a
z
)
(
2
s
b
v
b
y
+
2
v
b
x
v
b
z
)
+
(
s
a
2
−
v
a
x
2
−
v
a
y
2
+
v
a
z
2
)
(
s
b
2
−
v
b
x
2
−
v
b
y
2
+
v
b
z
2
)
]
\left[\begin{matrix}\left(2 s_{a} v_{ay} + 2 v_{ax} v_{az}\right) \left(- 2 s_{b} v_{by} + 2 v_{bx} v_{bz}\right) + \left(- 2 s_{a} v_{az} + 2 v_{ax} v_{ay}\right) \left(2 s_{b} v_{bz} + 2 v_{bx} v_{by}\right) + \left(s_{a}^{2} + v_{ax}^{2} - v_{ay}^{2} - v_{az}^{2}\right) \left(s_{b}^{2} + v_{bx}^{2} - v_{by}^{2} - v_{bz}^{2}\right) & \left(2 s_{a} v_{ay} + 2 v_{ax} v_{az}\right) \left(2 s_{b} v_{bx} + 2 v_{by} v_{bz}\right) + \left(- 2 s_{a} v_{az} + 2 v_{ax} v_{ay}\right) \left(s_{b}^{2} - v_{bx}^{2} + v_{by}^{2} - v_{bz}^{2}\right) + \left(- 2 s_{b} v_{bz} + 2 v_{bx} v_{by}\right) \left(s_{a}^{2} + v_{ax}^{2} - v_{ay}^{2} - v_{az}^{2}\right) & \left(2 s_{a} v_{ay} + 2 v_{ax} v_{az}\right) \left(s_{b}^{2} - v_{bx}^{2} - v_{by}^{2} + v_{bz}^{2}\right) + \left(- 2 s_{a} v_{az} + 2 v_{ax} v_{ay}\right) \left(- 2 s_{b} v_{bx} + 2 v_{by} v_{bz}\right) + \left(2 s_{b} v_{by} + 2 v_{bx} v_{bz}\right) \left(s_{a}^{2} + v_{ax}^{2} - v_{ay}^{2} - v_{az}^{2}\right)\\\left(- 2 s_{a} v_{ax} + 2 v_{ay} v_{az}\right) \left(- 2 s_{b} v_{by} + 2 v_{bx} v_{bz}\right) + \left(2 s_{a} v_{az} + 2 v_{ax} v_{ay}\right) \left(s_{b}^{2} + v_{bx}^{2} - v_{by}^{2} - v_{bz}^{2}\right) + \left(2 s_{b} v_{bz} + 2 v_{bx} v_{by}\right) \left(s_{a}^{2} - v_{ax}^{2} + v_{ay}^{2} - v_{az}^{2}\right) & \left(- 2 s_{a} v_{ax} + 2 v_{ay} v_{az}\right) \left(2 s_{b} v_{bx} + 2 v_{by} v_{bz}\right) + \left(2 s_{a} v_{az} + 2 v_{ax} v_{ay}\right) \left(- 2 s_{b} v_{bz} + 2 v_{bx} v_{by}\right) + \left(s_{a}^{2} - v_{ax}^{2} + v_{ay}^{2} - v_{az}^{2}\right) \left(s_{b}^{2} - v_{bx}^{2} + v_{by}^{2} - v_{bz}^{2}\right) & \left(- 2 s_{a} v_{ax} + 2 v_{ay} v_{az}\right) \left(s_{b}^{2} - v_{bx}^{2} - v_{by}^{2} + v_{bz}^{2}\right) + \left(2 s_{a} v_{az} + 2 v_{ax} v_{ay}\right) \left(2 s_{b} v_{by} + 2 v_{bx} v_{bz}\right) + \left(- 2 s_{b} v_{bx} + 2 v_{by} v_{bz}\right) \left(s_{a}^{2} - v_{ax}^{2} + v_{ay}^{2} - v_{az}^{2}\right)\\\left(2 s_{a} v_{ax} + 2 v_{ay} v_{az}\right) \left(2 s_{b} v_{bz} + 2 v_{bx} v_{by}\right) + \left(- 2 s_{a} v_{ay} + 2 v_{ax} v_{az}\right) \left(s_{b}^{2} + v_{bx}^{2} - v_{by}^{2} - v_{bz}^{2}\right) + \left(- 2 s_{b} v_{by} + 2 v_{bx} v_{bz}\right) \left(s_{a}^{2} - v_{ax}^{2} - v_{ay}^{2} + v_{az}^{2}\right) & \left(2 s_{a} v_{ax} + 2 v_{ay} v_{az}\right) \left(s_{b}^{2} - v_{bx}^{2} + v_{by}^{2} - v_{bz}^{2}\right) + \left(- 2 s_{a} v_{ay} + 2 v_{ax} v_{az}\right) \left(- 2 s_{b} v_{bz} + 2 v_{bx} v_{by}\right) + \left(2 s_{b} v_{bx} + 2 v_{by} v_{bz}\right) \left(s_{a}^{2} - v_{ax}^{2} - v_{ay}^{2} + v_{az}^{2}\right) & \left(2 s_{a} v_{ax} + 2 v_{ay} v_{az}\right) \left(- 2 s_{b} v_{bx} + 2 v_{by} v_{bz}\right) + \left(- 2 s_{a} v_{ay} + 2 v_{ax} v_{az}\right) \left(2 s_{b} v_{by} + 2 v_{bx} v_{bz}\right) + \left(s_{a}^{2} - v_{ax}^{2} - v_{ay}^{2} + v_{az}^{2}\right) \left(s_{b}^{2} - v_{bx}^{2} - v_{by}^{2} + v_{bz}^{2}\right)\end{matrix}\right]
(2savay+2vaxvaz)(−2sbvby+2vbxvbz)+(−2savaz+2vaxvay)(2sbvbz+2vbxvby)+(sa2+vax2−vay2−vaz2)(sb2+vbx2−vby2−vbz2)(−2savax+2vayvaz)(−2sbvby+2vbxvbz)+(2savaz+2vaxvay)(sb2+vbx2−vby2−vbz2)+(2sbvbz+2vbxvby)(sa2−vax2+vay2−vaz2)(2savax+2vayvaz)(2sbvbz+2vbxvby)+(−2savay+2vaxvaz)(sb2+vbx2−vby2−vbz2)+(−2sbvby+2vbxvbz)(sa2−vax2−vay2+vaz2)(2savay+2vaxvaz)(2sbvbx+2vbyvbz)+(−2savaz+2vaxvay)(sb2−vbx2+vby2−vbz2)+(−2sbvbz+2vbxvby)(sa2+vax2−vay2−vaz2)(−2savax+2vayvaz)(2sbvbx+2vbyvbz)+(2savaz+2vaxvay)(−2sbvbz+2vbxvby)+(sa2−vax2+vay2−vaz2)(sb2−vbx2+vby2−vbz2)(2savax+2vayvaz)(sb2−vbx2+vby2−vbz2)+(−2savay+2vaxvaz)(−2sbvbz+2vbxvby)+(2sbvbx+2vbyvbz)(sa2−vax2−vay2+vaz2)(2savay+2vaxvaz)(sb2−vbx2−vby2+vbz2)+(−2savaz+2vaxvay)(−2sbvbx+2vbyvbz)+(2sbvby+2vbxvbz)(sa2+vax2−vay2−vaz2)(−2savax+2vayvaz)(sb2−vbx2−vby2+vbz2)+(2savaz+2vaxvay)(2sbvby+2vbxvbz)+(−2sbvbx+2vbyvbz)(sa2−vax2+vay2−vaz2)(2savax+2vayvaz)(−2sbvbx+2vbyvbz)+(−2savay+2vaxvaz)(2sbvby+2vbxvbz)+(sa2−vax2−vay2+vaz2)(sb2−vbx2−vby2+vbz2)







![[RTOS移植]--STM32F767移植RTThread](https://img-blog.csdnimg.cn/5a0173984eae44cc90e9d4a3c29b313c.png)