文章目录
- 二叉树的前序遍历
- 递归
- 迭代
- Morris遍历
- 二叉树的中序遍历
- 递归
- 迭代
- Morris遍历
- 二叉树的后序遍历
- 递归
- 迭代
- Morris遍历
二叉树的前序遍历
力扣传送门:
https://leetcode.cn/problems/binary-tree-preorder-traversal/description/
递归
递归的解法非常简单,只需要记住这是前序遍历,因此只要记住在访问节点的时候是按照根左右的顺序访问的,因此首先记录根节点,然后递归遍历左子树和右子树。
class Solution {
public:
vector<int> res;
void dfs(TreeNode* root)
{
if (root==nullptr)
{
return;
}
res.emplace_back(root->val);
dfs(root->left);
dfs(root->right);
}
vector<int> preorderTraversal(TreeNode* root) {
dfs(root);
return res;
}
};
迭代
迭代的过程其实就是隐式的维护一个栈。
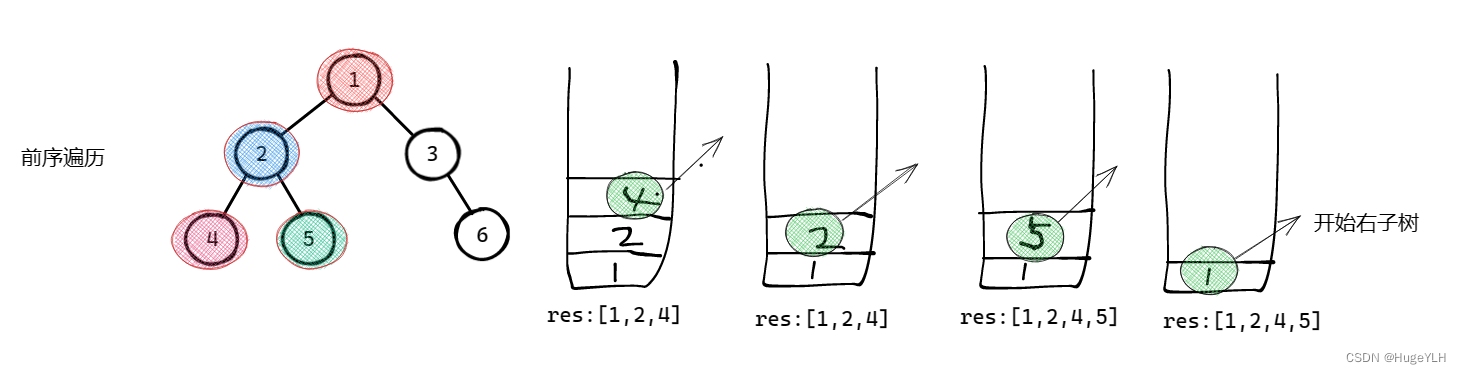
写法一: 前序遍历:依次处理根左右
首先不断搜索节点的左孩子,然后记录当前节点的值,这就是前序遍历的访问根节点的过程。搜索到左孩子之后加入到栈中,然后利用栈的先进先出的特性, 栈顶节点就是最左的叶子节点(如果有的话),这就是访问左子树的过程,然后依次弹出每一个栈顶节点,访问其右子节点,这就是访问右子树,然后重复这个循环。
class Solution {
public:
vector<int> res;
vector<int> preorderTraversal(TreeNode* root) {
stack<TreeNode*> sp;
vector<int> res;
while (root || !sp.empty())
{
while (root)
{
res.emplace_back(root->val);
sp.emplace(root);
root=root->left;
}
root=sp.top();
sp.pop();
root=root->right;
}
return res;
}
};
写法二:
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
vector<int> res;
if (root==nullptr)
{
return res;
}
stack<TreeNode*> sp;
sp.emplace(root);
while (!sp.empty())
{
TreeNode* node=sp.top();
sp.pop();
res.emplace_back(node->val);
//首先把右子树放入栈中,因为是前序遍历,因此栈中要满足栈顶是左子树,往下才是右子树
if (node->right)
{
sp.emplace(node->right);
}
if (node->left)
{
sp.emplace(node->left);
}
}
return res;
}
};
Morris遍历
前序遍历的Morris的过程:
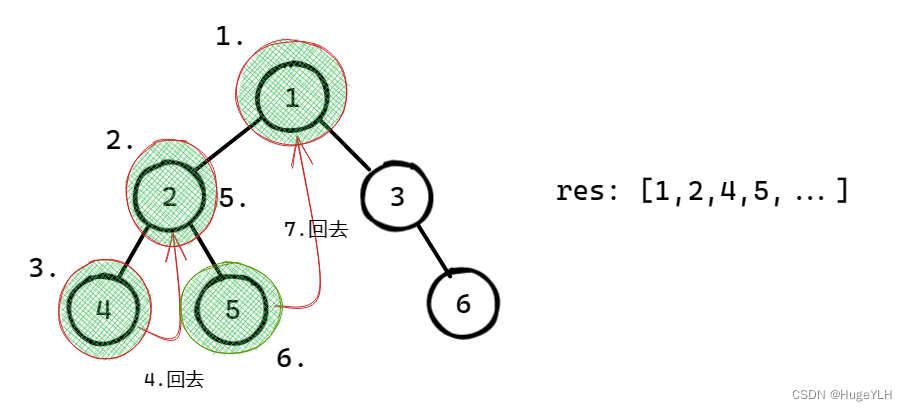
-
首先判断当前节点的左子树为空,则说明当前位于叶子节点上,将当前节点放入结果数组中,遍历其右子树
-
当前节点的左子树不为空,找到中序遍历节点的当前节点的前驱节点,令它为thread(线索节点)。
- 如果thread的右子树为空,则让thread的右子树指定当前节点,当前节点的值放入到结果数组中(根节点的存储),再将当前节点移动到当前节点的左子树节点
- 如果thread的右子树不为空,则让当前节点移动到其右子树节点,让thread的右子树指向空。
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
vector<int> res;
while (root)
{
//左子树不为空
if (root->left)
{
//找到线索节点(当前节点的左子树的最右节点,即是中序遍历的前驱节点)
TreeNode* thread=root->left;
while (thread->right!=nullptr &&thread->right!=root)
{
thread=thread->right;
}
//thread为空,则连接线索
if (thread->right==nullptr)
{
//建立线索:连接右子树
thread->right=root;
//在进入左右子树之前,首先存储根节点:前序遍历
res.emplace_back(root->val);
root=root->left;
}
else
{
//左子树遍历完成,断开连接
root=root->right;
thread->right=nullptr;
}
}
//左子树为空,到达了叶子节点,保存节点的值,根据线索返回
else
{
//到达了叶子节点
res.emplace_back(root->val);
root=root->right;
}
}
return res;
}
};
二叉树的中序遍历
力扣传送门:
https://leetcode.cn/problems/binary-tree-inorder-traversal/description/
递归
递归的解法非常简单,只需要记住这是中序遍历,因此只要记住在访问节点的时候是按照左根右的顺序访问的,因此首先记录左子树,然后记录根节点,最后递归遍历右子树。
class Solution {
public:
vector<int> res;
void dfs(TreeNode* root)
{
if (root==nullptr)
{
return;
}
//左 根 右
dfs(root->left);
res.emplace_back(root->val);
dfs(root->right);
}
vector<int> preorderTraversal(TreeNode* root) {
dfs(root);
return res;
}
};
迭代
隐式的维护一个栈。
类似于前序遍历一样,中序遍历我们只需要在其访问根节点的时候,把根节点的节点放入结果数组中即可,可以比较以下 前序和中序遍历时
res.emplace_back(root->val);
这条语句出现的位置。
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> res;
stack<TreeNode*> sp;
while (root || !sp.empty())
{
while (root)
{
//如果是前序遍历,则res的插入要放在这里(即在左子树和右子树之前)。
sp.emplace(root);
root=root->left;
}
root=sp.top();
sp.pop();
//中序遍历:左根右,根在左子树之后,右子树之前
res.emplace_back(root->val);
root=root->right;
}
return res;
}
};
Morris遍历
中序遍历Morris过程:
-
首先判断当前节点的左子树为空,则说明当前位于叶子节点上,将当前节点放入结果数组中,遍历其右子树
-
当前节点的左子树不为空,找到中序遍历节点的当前节点的前驱节点,令它为thread(线索节点)。
- 如果thread的右子树为空,则让thread的右子树指定当前节点,将当前节点移动到当前节点的左子树节点
- 如果thread的右子树不为空,则让当前节点移动到其右子树节点,当前节点的值放入到结果数组中(根节点的存储),让thread的右子树指向空。
同样前序和中序的遍历只有一个敌方不同:
res.emplace_back(root->val);
可以比较一下前序和中序Morris的遍历时这条语句的位置。
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> res;
while (root)
{
if (root->left)
{
TreeNode* thread=root->left;
while (thread->right!=nullptr &&thread->right!=root)
{
thread=thread->right;
}
if (thread->right==nullptr)
{
//建立线索:连接右子树
//前序遍历:res的插入要放在这里
thread->right=root;
root=root->left;
}
else
{
//左子树遍历完成,断开连接
//中序遍历: 这条语句放在这里(当前else表示左子树遍历完了,接着要遍历右子树,所以在左右之间,首先存储根节点)
res.emplace_back(root->val); //左右之间:存储根节点
root=root->right; //遍历右子树
thread->right=nullptr;
}
}
else
{
//到达了叶子节点
res.emplace_back(root->val);
root=root->right;
}
}
return res;
}
};
二叉树的后序遍历
力扣传送门:
https://leetcode.cn/problems/binary-tree-postorder-traversal/description/
递归
递归的解法非常简单,只需要记住这是后序遍历,因此只要记住在访问节点的时候是按照左右根的顺序访问的,因此首先递归遍历左子树和右子树,最后记录根节点。
class Solution {
public:
vector<int> res;
void dfs(TreeNode* root)
{
if (root==nullptr)
{
return;
}
dfs(root->left);
dfs(root->right);
res.emplace_back(root->val);
}
vector<int> preorderTraversal(TreeNode* root) {
dfs(root);
return res;
}
};
迭代
迭代的过程是隐式的维护一个栈。
方法一:利用一个prev临时节点保存位置
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
stack<TreeNode*> sp;
TreeNode* prev;
vector<int> res;
while (root ||!sp.empty())
{
while (root)
{
sp.emplace(root);
root=root->left;
}
root=sp.top();
sp.pop();
if (root->right==nullptr || root->right==prev)
{
res.emplace_back(root->val);
prev=root;
root=nullptr;
}
else
{
sp.emplace(root);
root=root->right;
}
}
return res;
}
};
方法二: 翻转
后序遍历的顺序是 左右根 ,因此我们想要得到 左右根的遍历顺序,可以首先得到 根右左的遍历顺序,然后进行一次翻转(自行证明,画个图即可);根右左又可以看成是前序遍历的 根左右,只需把 左和右子树的遍历互换一下位置即可。
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
vector<int> res;
if (root==nullptr)
{
return res;
}
stack<TreeNode*> sp;
sp.emplace(root);
while (!sp.empty())
{
TreeNode* node=sp.top();
sp.pop();
//根
res.emplace_back(node->val);
//右:注意这里首先left入栈
if (node->left)
{
sp.emplace(node->left);
}
//左:之后让right入栈,想想一下在栈中就会出现栈顶是右子树,往下是左子树
//因此这里就成功的把根左右变成了 《根右左》
if (node->right)
{
sp.emplace(node->right);
}
}
//根右左 进行一次翻转: 左右跟:后序遍历
reverse(res.begin(),res.end());
return res;
}
};
Morris遍历
后序遍历的Morris比较复杂,因此在这里使用跟迭代的方法二类似的办法:翻转。
后序遍历:左右根,因此首先求出 根右左,然后进行一次翻转即可,根右左又可以看作是根左右的右子树和左子树进行一次互换位置即可,因此就是前序遍历的Morris,把左右子树的遍历过程进行一次调换即可,得到了根右左的序列,最后再进行一次翻转,得到了左右根的后序遍历。
总结: 把前序遍历的Morris过程中的左右互换,最后进行一次翻转。
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
vector<int> res;
while (root)
{
if (root->right)
{
TreeNode* thread=root->right;
while (thread->left!=nullptr &&thread->left!=root)
{
thread=thread->left;
}
if (thread->left==nullptr)
{
//建立线索:连接左子树
thread->left=root;
res.emplace_back(root->val);
root=root->right;
}
else
{
//右子树遍历完成,断开连接
root=root->left;
thread->left=nullptr;
}
}
else
{
//到达了叶子节点
res.emplace_back(root->val);
root=root->left;
}
}
reverse(res.begin(),res.end());
return res;
}
};


![Rabbit客户端操作不同交换机[包含延迟类型]](https://img-blog.csdnimg.cn/b61baf95e18a431a82cd1ae06c2d1751.png)

![[牛客复盘] 牛客2022跨年场 20221212](https://img-blog.csdnimg.cn/07c2880706ad4a5eb2363567714be2e9.png)





![[ XSS-labs通关宝典 ] xss-labs 通关宝典之 less1 - less5](https://img-blog.csdnimg.cn/a125b39655294c87bb54d2a8c7691701.png)
