刷题的第十四天,希望自己能够不断坚持下去,迎来蜕变。😀😀😀
刷题语言:C++
Day14 任务
● 110.平衡二叉树
● 257. 二叉树的所有路径
● 404.左叶子之和
1 平衡二叉树
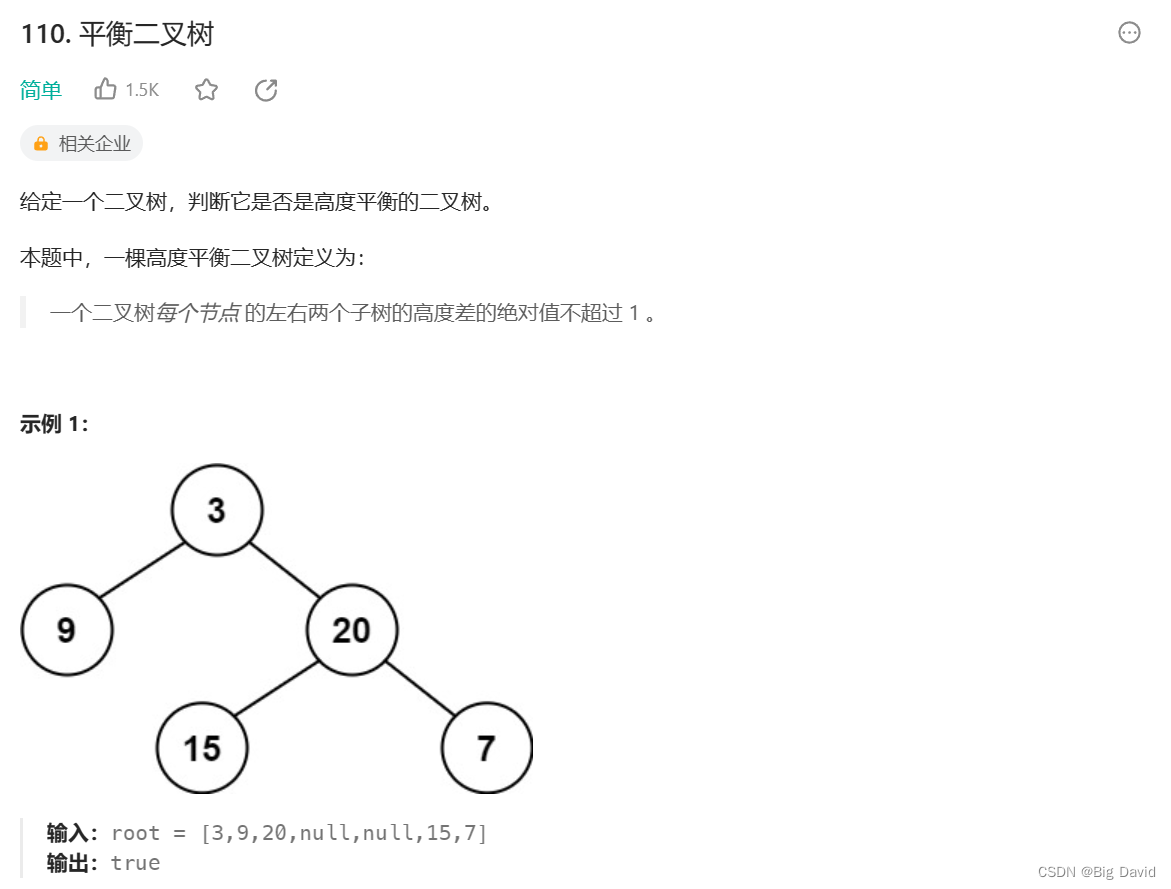
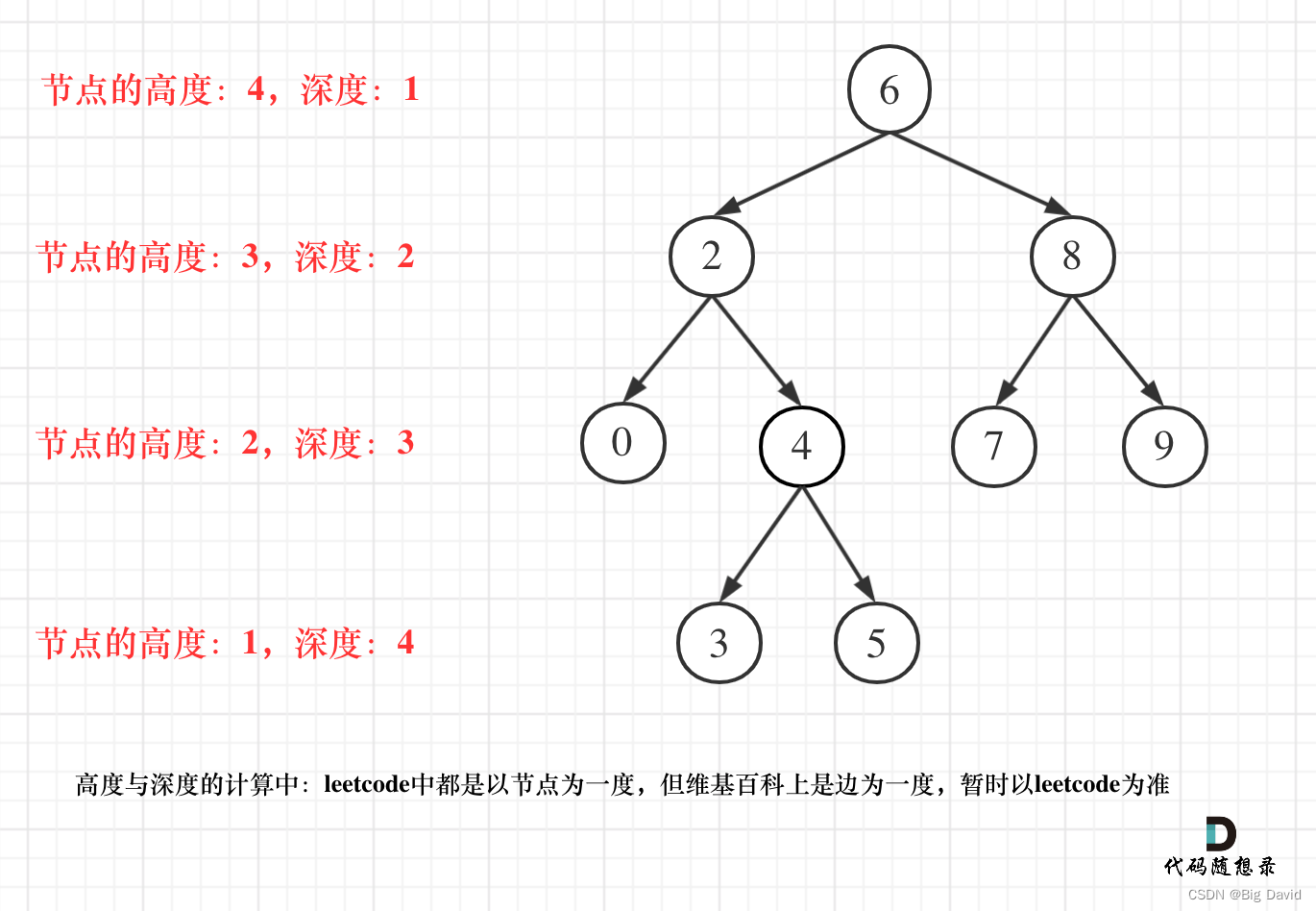
二叉树节点的深度:指从根节点到该节点的最长简单路径边的条数
二叉树节点的高度:指从该节点到叶子节点的最长简单路径边的条数
思路:
递归法
(1)明确递归函数的参数和返回值
参数:当前传入节点。 返回值:以当前传入节点为根节点的树的高度。
如果已经不是二叉平衡树了,可以返回-1 来标记已经不符合平衡树的规则了
// -1 表示已经不是平衡二叉树了,否则返回值是以该节点为根节点树的高度
int getHeight(TreeNode* node)
(2)明确终止条件:遇到空节点了为终止,返回0,表示当前节点为根节点的树高度为0
if (node == NULL) return 0;
(3)明确单层递归的逻辑
判断当前传入节点为根节点的二叉树是否是平衡二叉树?
左子树高度和其右子树高度的差值
分别求出其左右子树的高度,然后如果差值小于等于1,则返回当前二叉树的高度,否则返回-1,表示已经不是二叉平衡树了
int leftHeight = getHeight(node->left); // 左
if (leftHeight == -1) return -1;
int rightHeight = getHeight(node->right); // 右
if (rightHeight == -1) return -1;
int result;
if (abs(leftHeight - rightHeight) > 1)
{
result = -1;
}
else
{
result = 1 + max(leftHeight, rightHeight);
}
return result;
递归的函数传入节点指针,返回以该节点为根节点的二叉树的高度,如果不是二叉平衡树,则返回-1
求深度适合用前序遍历,而求高度适合用后序遍历
C++:
后序遍历
class Solution {
public:
// 返回以该节点为根节点的二叉树的高度,如果不是平衡二叉树了则返回-1
int getHeight(TreeNode* node)
{
if (node == NULL) return 0;
int leftHeight = getHeight(node->left);
if (leftHeight == -1) return -1;
int rightHeight = getHeight(node->right);
if (rightHeight == -1) return -1;
int result;
if (abs(leftHeight - rightHeight) > 1) result = -1;
else
{
result = 1 + max(leftHeight, rightHeight);
}
return result;
}
bool isBalanced(TreeNode* root) {
return getHeight(root) == -1 ? false : true;
}
};
精简版本C++:
class Solution {
public:
int getHeight(TreeNode* node)
{
if (node == NULL) return 0;
int leftHeight = getHeight(node->left);
if (leftHeight == -1) return -1;
int rightHeight = getHeight(node->right);
if (rightHeight == -1) return -1;
int result;
return abs(leftHeight - rightHeight) > 1 ? -1 : 1 + max(leftHeight, rightHeight);
}
bool isBalanced(TreeNode* root) {
return getHeight(root) == -1 ? false : true;
}
};
2 二叉树的所有路径
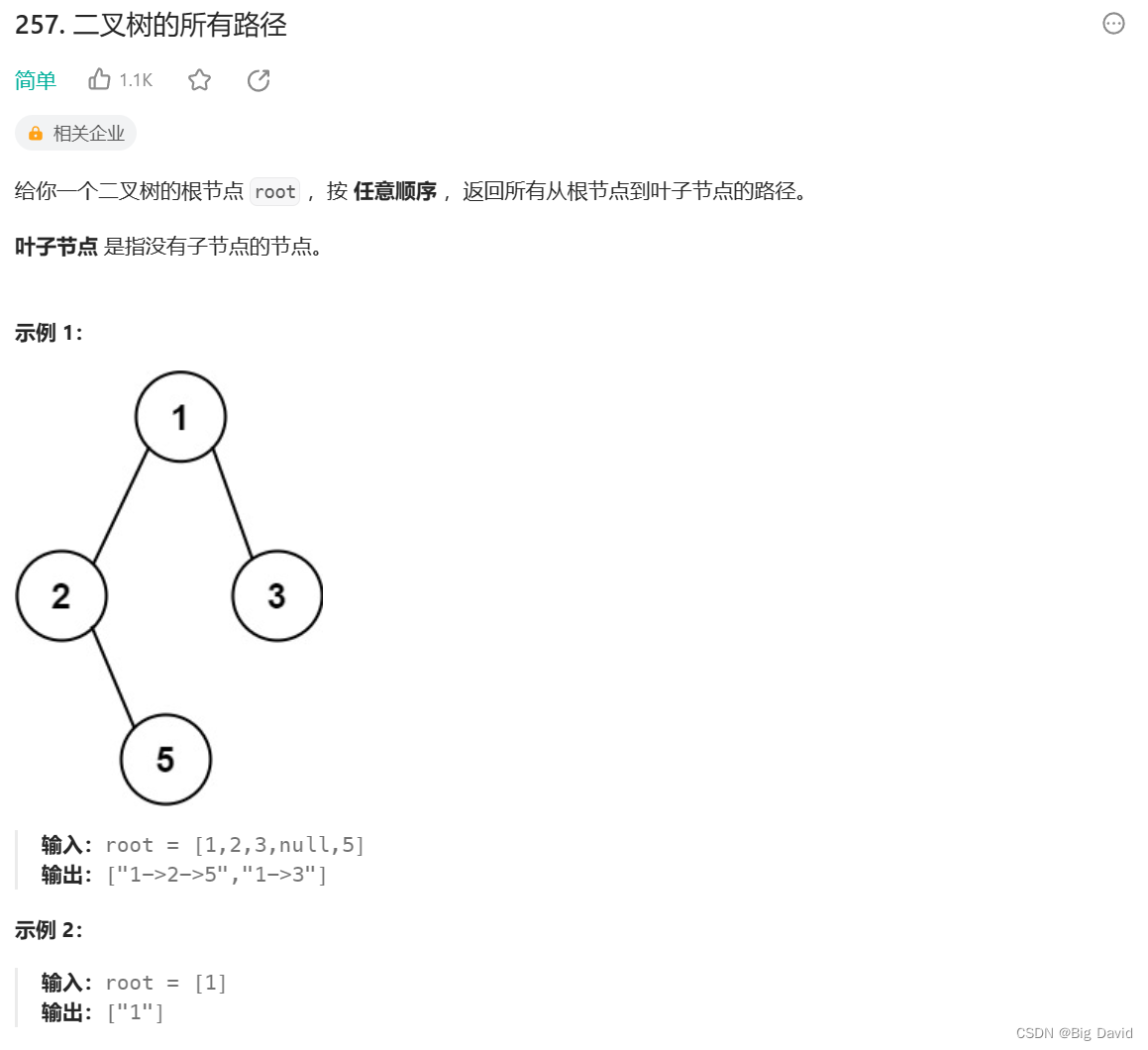
思路:
本道题要求根节点到叶子的路径,需要前序遍历,方便父节点指向孩子节点,找到对应的路径。
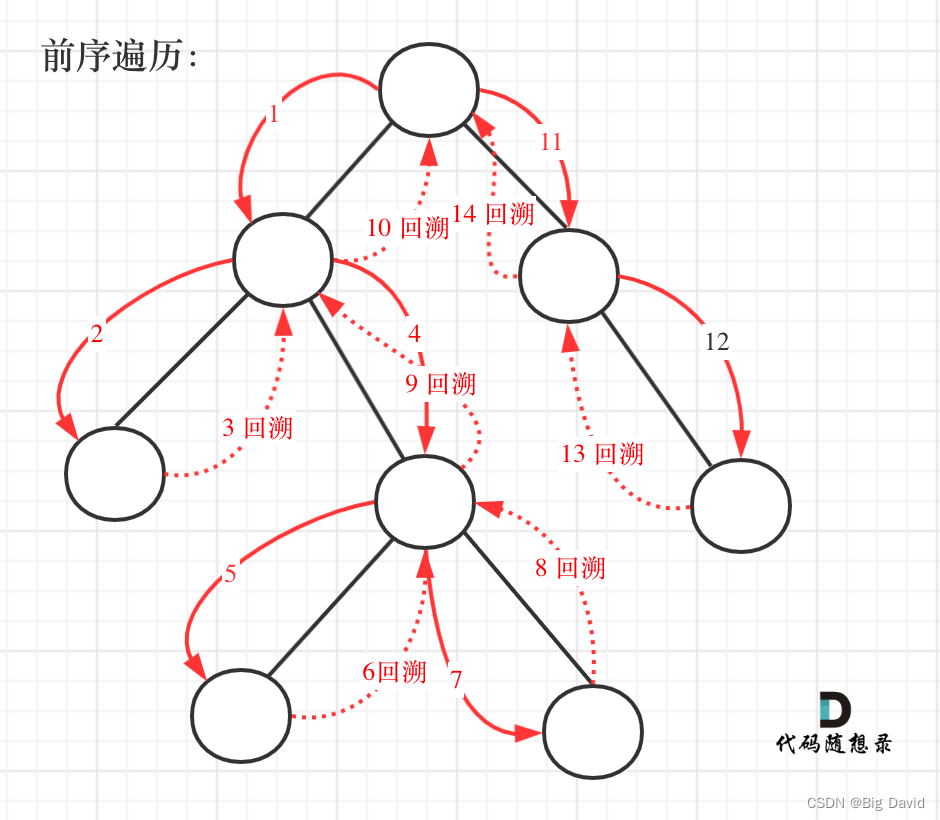
递归法:
(1)递归函数参数和返回值
参数:根节点、记录每一条路径的path、存放结果集的result。这里递归不需要返回值
void traversal(TreeNode* node, vector<int>& path, vector<string>& result)
(2)确定递归终止条件
本题要找到叶子节点,就开始结束的处理逻辑了(把路径放进result里)
找到叶子节点:当node不为空,左右孩子都为空的时候
if (node->left == NULL && node->right == NULL) {
//终止处理逻辑
}
终止处理的逻辑:
用vector 结构path来记录路径,把vector 结构的path转为string格式,再把这个string 放进 result里。
使用vector 结构来记录路径,是因为在下面处理单层递归逻辑的时候,要做回溯,使用vector方便来做回溯
// 遇到叶子节点
if (node->left == NULL && node->right == NULL) {
//终止处理逻辑
string sPath;
for (int i = 0; i < path.size() - 1; i++)// 将path里记录的路径转为string格式
{
sPath += to_string(path[i]);
sPath += "->";
}
sPath += to_string(path[path.size() - 1]);// 记录最后一个节点(叶子节点)
result.push_back(sPath);
return;
}
(3)确定单层递归逻辑
前序遍历,需要先处理中间节点,
中间节点就是要记录路径上的节点,先放进path中
然后是递归和回溯的过程,上面说过没有判断node是否为空,那么在这里递归的时候,如果为空就不进行下一层递归了。
递归完,要做回溯,因为path 不能一直加入节点,它还要删节点,然后才能加入新的节点。
回溯和递归是一一对应的,有一个递归,就要有一个回溯
if (node->left)
{
traversal(node->left, path, result);
path.pop_back();// 回溯
}
if (node->right)
{
traversal(node->right, path, result);
path.pop_back();// 回溯
}
C++:
class Solution {
public:
void traversal(TreeNode* node, vector<int>& path, vector<string>& result)
{
path.push_back(node->val);// 中 最后一个节点也要加入到path中
if (node->left == NULL && node->right == NULL)
{
string sPath;
for (int i = 0; i < path.size() - 1; i++)
{
sPath += to_string(path[i]);
sPath += "->";
}
sPath += to_string(path[path.size() - 1]);
result.push_back(sPath);
}
if (node->left)// 左
{
traversal(node->left, path, result);
path.pop_back();// 回溯
}
if (node->right)// 右
{
traversal(node->right, path, result);
path.pop_back();// 回溯
}
}
vector<string> binaryTreePaths(TreeNode* root) {
vector<int> path;
vector<string> result;
if (root == NULL) return result;
traversal(root, path, result);
return result;
}
};
精简版本C++:
class Solution {
public:
void traversal(TreeNode* node, string path, vector<string>& result)
{
path += to_string(node->val); // 中
if (node->left == NULL && node->right == NULL) {
result.push_back(path);
return;
}
if (node->left) traversal(node->left, path + "->", result); // 左
if (node->right) traversal(node->right, path + "->", result); // 右
}
vector<string> binaryTreePaths(TreeNode* root) {
vector<string> result;
string path;
if (root == NULL) return result;
traversal(root, path, result);
return result;
}
};
vector类型的path,不管 每次 路径收集的数字是几位数,总之一定是int,所以就一次 pop_back就可以
3 左叶子之和

思路:
注意是判断左叶子,不是二叉树左侧节点,所以不要上来想着层序遍历。
左叶子:节点A的左孩子不为空,且左孩子的左右孩子都为空(说明是叶子节点),那么A节点的左孩子为左叶子节点
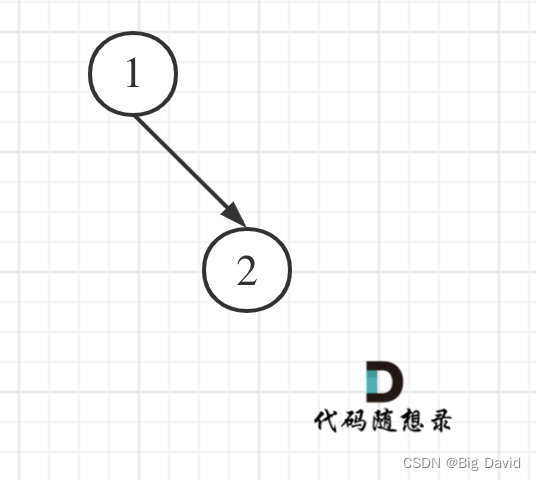
该左叶子之和为0,因为这棵树根本没有左叶子!
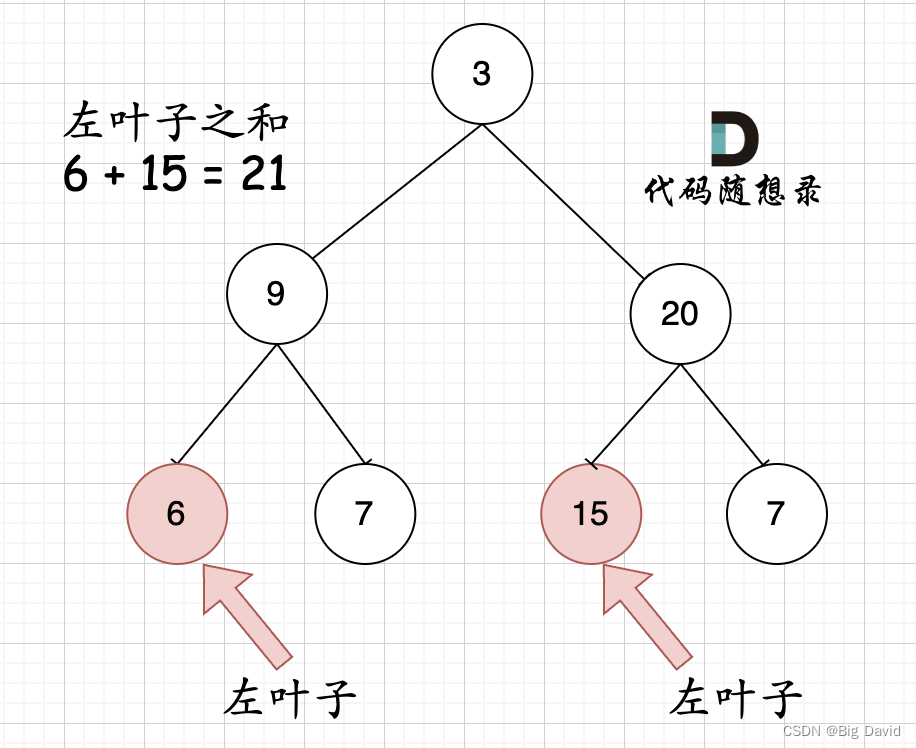
如果该节点的左节点不为空,该节点的左节点的左节点为空,该节点的左节点的右节点为空,则找到了一个左叶子
if (node->left != NULL && node->left->left == NULL && node->left->right == NULL)
{
左叶子节点处理逻辑
}
递归法:
递归的遍历顺序为后序遍历(左右中),需要通过递归函数的返回值累加求取左叶子数值之和
(1)确定递归函数的参数和返回值
判断一个树的左叶子节点之和,那么一定要传入树的根节点,递归函数的返回值为数值之和,所以为int
(2)确定终止条件
遍历到空节点,那么左叶子值一定是0
if (root == NULL) return 0;
只有当前遍历的节点是父节点,才能判断其子节点是不是左叶子。 所以如果当前遍历的节点是叶子节点,那其左叶子也必定是0
if (root == NULL) return 0;
if (root->left == NULL && root->right == NULL) return 0;
(3)确定单层递归的逻辑
当遇到左叶子节点的时候,记录数值,然后通过递归求取左子树左叶子之和,和 右子树左叶子之和,相加便是整个树的左叶子之和
int leftNum = sumOfLeftLeaves(root->left); // 左
if (root->left != NULL && root->left->left == NULL && root->left->right)
{
leftNum = root->left->val;
}
int rightNum = sumOfLeftLeaves(root->right); // 右
int sum = leftNum + rightNum;// 中
return sum;
C++:
class Solution {
public:
int sumOfLeftLeaves(TreeNode* root) {
if (root == NULL) return 0;
if (root->left == NULL && root->right == NULL) return 0;
int leftNum = sumOfLeftLeaves(root->left);// 左
if (root->left != NULL && root->left->left == NULL && root->left->right == NULL)// 左子树就是一个左叶子的情况
{
leftNum = root->left->val;
}
int rightNum = sumOfLeftLeaves(root->right);// 右
int sum = leftNum + rightNum;// 中
return sum;
}
};
精简C++:
class Solution {
public:
int sumOfLeftLeaves(TreeNode* root) {
if (root == NULL) return 0;
int leftValue = 0;
if (root->left != NULL && root->left->left == NULL && root->left->right == NULL) {
leftValue = root->left->val;
}
return leftValue + sumOfLeftLeaves(root->left) + sumOfLeftLeaves(root->right);
}
};
鼓励坚持十五天的自己😀😀😀