树形动态规划

树形动态规划一般用于处理求树上最优值的问题。大多数动态规划问题都是在一维二维这种规则的背景下的，可以解决的问题比较局限，而树作为一种特殊的图，可以描述比较复杂的关系，再加上树的递归定义，是一种非常合适进行动态规划处理的数据结构。

具体来说，在树形动态规划当中，一般先算子树再进行合并。与树的后序遍历相似，都是先遍历子树，遍历完之后将子树的值传给父亲。简单来说就是先递归访问所有子树，再在根上合并。

了解了树形动态规划的基本思想后，下面来看一个树形动态规划的例题。

经典例题

题目链接

没有上司的舞会

题目描述

某大学有 $n$ 个职员，编号为 $1\dots n$。

他们之间有从属关系，也就是说他们的关系就像一棵以校长为根的树，父结点就是子结点的直接上司。

现在有个周年庆宴会，宴会每邀请来一个职员都会增加一定的快乐指数 $h_i$，但是呢，如果某个职员的直接上司来参加舞会了，那么这个职员就无论如何也不肯来参加舞会了。

所以，请你编程计算，邀请哪些职员可以使快乐指数最大，求最大的快乐指数。

输入格式

输入的第一行是一个整数 $n$。

第 $2$ 到第 $(n+1)$ 行，每行一个整数，第 $(i+1)$ 行的整数表示 $i$ 号职员的快乐指数 $h_i$。

第 $(n+2)$ 到第 $2n$ 行，每行输入一对整数 $l,k$，代表 $k$ 是 $l$ 的直接上司。

输出格式

输出一行一个整数代表最大的快乐指数。

样例 #1

样例输入 #1

7
1
1
1
1
1
1
1
1 3
2 3
6 4
7 4
4 5
3 5

样例输出 #1

5

提示

数据规模与约定

对于 $100\%$ 的数据，保证 $1\le n\le 6\times 10^3$，$-128\le h_i\le 127$，$1\le l,k\le n$，且给出的关系一定是一棵树。

算法思想

从给出的测试样例，可以构建出这样一棵树。

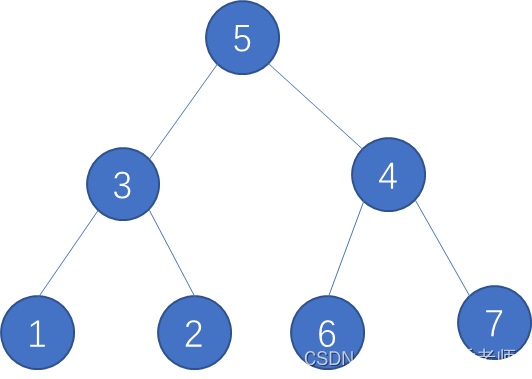
从图中可以看出，$1、2$的上司是$3$，$6、7$的上司是$4$，如果$3、4$不参加舞会的话，邀请$1、2、5、6、7$，可以使快乐指数最大为$5$。由此可见：

• 对树中每个结点有$2$种选择，邀请或者不邀请
• 结点的选择与否会影响其子结点：某个职员的直接上司来参加舞会了，那么这个职员就无论如何也不肯来参加舞会

因此，在状态表示时需要考虑树的整体收益，以及结点的状态（邀请或者不邀请）。

状态表示

• $f[i][0]$表示以$i$为根的子树，在不邀请根结点$i$时的最大快乐指数
• $f[i][1]$表示以$i$为根的子树，在邀请根结点$i$时的最大快乐指数

不妨设整棵树的根结点为$r$，那么最终答案是$f[r][0]$和$f[r][1]$的最大值。

状态计算

对于$i$为根的子树，考虑当前的根结点$i$的状态：

• 如果不邀请$i$，那么可以选择邀请或者不邀请其子结点$j$，因此可以递归计算出$f[j][0]$和$f[j][1]$，取二者的最大值进行累加，即$f[i][0]=\sum max(f[j][0],f[j][1])$，其中$j$是$i$的所有子结点。
• 如果邀请$i$，那么不能邀请其子结点$j$，因此可以递归计算出$f[j][0]$，$f[i][0]=\sum (f[j][0])$，其中$j$是$i$的所有子结点。

初始状态

$f[i][1]$表示在邀请根结点$i$时的最大快乐指数，其初始值为$h[i]$。

时间复杂度

由于在递归的过程每个点都只会算一次，所以总的时间复杂度为 $O(n)$。

代码实现

#include <iostream>
#include <vector>
using namespace std;

const int N = 6010;
int h[N]; //快乐指数
int fa[N]; //保存每个结点的父节点
//邻接表存储树
vector<int> g[N];
//f[i][0]表示以i为根的子树，在不邀请根结点i时的最大快乐指数
//f[i][1]表示以i为根的子树，在邀请根结点i时的最大快乐指数
int f[N][2];
void dfs(int i)
{
    f[i][1] = h[i]; //初始状态
    for(int j : g[i]) //遍历i的子结点
    {
        dfs(j); //递归计算以j为根的子树
        f[i][0] += max(f[j][0], f[j][1]);
        f[i][1] += f[j][0];
    }
}
int main()
{
    int n;
    cin >> n;
    //输入快乐指数
    for(int i = 1; i <= n; i ++) cin >> h[i];
    //构建树
    for(int i = 1; i < n; i ++)
    {
        int a, b;
        cin >> a >> b;
        g[b].push_back(a); //a是b的子结点
        fa[a] = b; //a的父节点是b
    }
    //确定根结点
    int r = 1;
    while(fa[r]) r = fa[r];
    dfs(r);
    cout << max(f[r][0], f[r][1]);
    return 0;
}