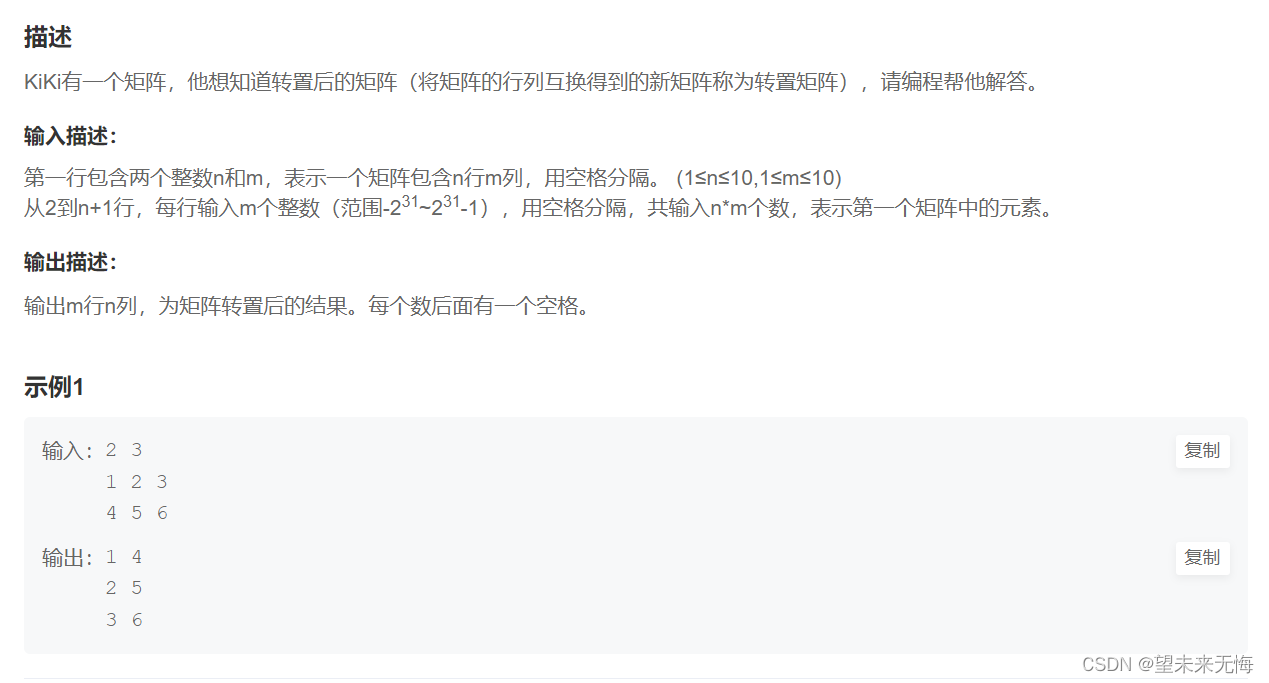
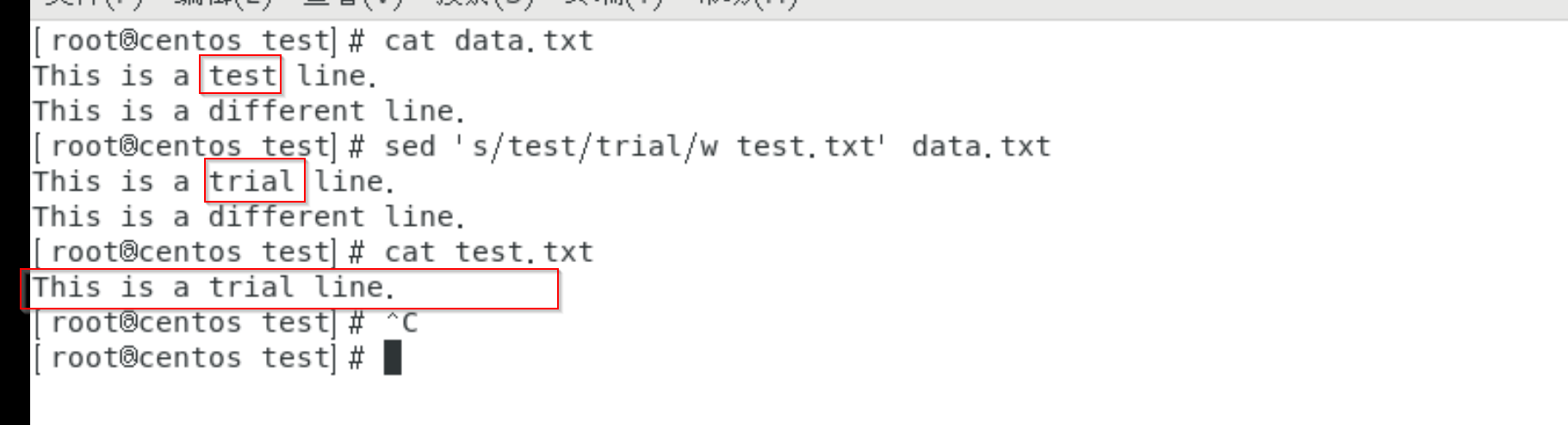
习题题目

答案
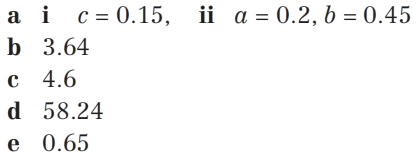
用到的概念:
概率之和等于1
E
(
x
)
=
∑
i
=
1
4
x
i
P
i
E(x)=\sum_{i=1}^4x_iP_i
E(x)=∑i=14xiPi
E
(
x
2
)
=
∑
i
=
1
4
x
i
2
P
i
E(x^2)=\sum_{i=1}^4x_i^2P_i
E(x2)=∑i=14xi2Pi
V
a
r
(
X
)
Var(X)
Var(X)
=
∑
i
=
1
4
(
x
i
−
x
‾
)
2
⋅
P
i
=\sum_{i=1}^4(x_i-\overline{x})^2·P_i
=∑i=14(xi−x)2⋅Pi
V
a
r
(
A
X
+
B
)
=
A
2
⋅
V
a
r
(
X
)
Var(AX+B)=A^2·Var(X)
Var(AX+B)=A2⋅Var(X)
习题(a)
E
(
x
)
=
−
2
a
+
0
∗
b
+
2
a
+
4
c
=
0.6
E(x)=-2a+0*b+2a+4c=0.6
E(x)=−2a+0∗b+2a+4c=0.6
c
=
0.15
c=0.15
c=0.15
E
(
x
2
)
=
4
a
+
0
b
+
4
a
+
16
c
=
4
E(x^2)=4a+0b+4a+16c=4
E(x2)=4a+0b+4a+16c=4
a
=
0.2
a=0.2
a=0.2
∵
a
+
b
+
a
+
c
=
1
∵a+b+a+c=1
∵a+b+a+c=1
∴
b
=
0.45
∴b=0.45
∴b=0.45
其中
E
(
x
)
E(x)
E(x)是总体的平均,
而
x
‾
是从总体抽取到的样本的平均
\overline{x}是从总体抽取到的样本的平均
x是从总体抽取到的样本的平均
这里
d
E
(
x
)
=
x
‾
=
0.6
dE(x)=\overline{x}=0.6
dE(x)=x=0.6
习题
(
b
)
习题(b)
习题(b)
V
a
r
(
X
)
Var(X)
Var(X)
=
∑
i
=
1
4
(
x
i
−
x
‾
)
2
⋅
P
i
=\sum_{i=1}^4(x_i-\overline{x})^2·P_i
=∑i=14(xi−x)2⋅Pi
=
∑
i
=
1
4
(
x
i
−
E
(
x
)
)
2
⋅
P
i
=\sum_{i=1}^4(x_i-E(x))^2·P_i
=∑i=14(xi−E(x))2⋅Pi
=
(
−
2
−
0.6
)
2
∗
0.2
+
(
0
−
0.6
)
2
∗
0.45
+
(
2
−
0.6
)
2
∗
0.2
+
(
4
−
0.6
)
2
∗
0.15
=(-2-0.6)^2*0.2+(0-0.6)^2*0.45+(2-0.6)^2*0.2+(4-0.6)^2*0.15
=(−2−0.6)2∗0.2+(0−0.6)2∗0.45+(2−0.6)2∗0.2+(4−0.6)2∗0.15
=
3.64
=3.64
=3.64
习题 ( c ) 习题(c) 习题(c)
E ( Y ) = E ( 7 − 4 X ) = 7 − 4 E ( x ) = 7 − 4 ∗ 0.6 = 4.6 E(Y)=E(7-4X)=7-4E(x)=7-4*0.6=4.6 E(Y)=E(7−4X)=7−4E(x)=7−4∗0.6=4.6
习题
(
d
)
习题(d)
习题(d)
V
a
r
(
Y
)
Var(Y)
Var(Y)
=
V
a
r
(
7
−
4
x
)
=Var(7-4x)
=Var(7−4x)
=
16
V
a
r
(
x
)
=16Var(x)
=16Var(x)
=
16
∗
3.64
=16*3.64
=16∗3.64
=
58.24
=58.24
=58.24
习题
(
e
)
习题(e)
习题(e)
P
(
Y
≥
0
)
P(Y≥0)
P(Y≥0)
=
P
(
7
−
4
X
≥
0
)
=P(7-4X≥0)
=P(7−4X≥0)
=
P
(
X
≤
7
4
)
=P(X≤\frac{7}{4})
=P(X≤47)
=
P
(
x
=
−
2
)
+
P
(
x
=
0
)
=P(x=-2)+P(x=0)
=P(x=−2)+P(x=0)
=
0.2
+
0.45
=
0.65
=0.2+0.45=0.65
=0.2+0.45=0.65