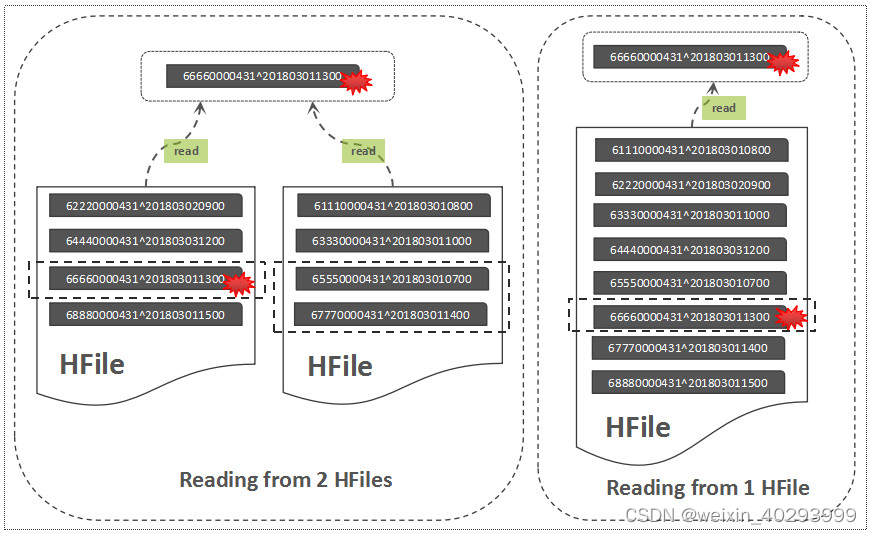
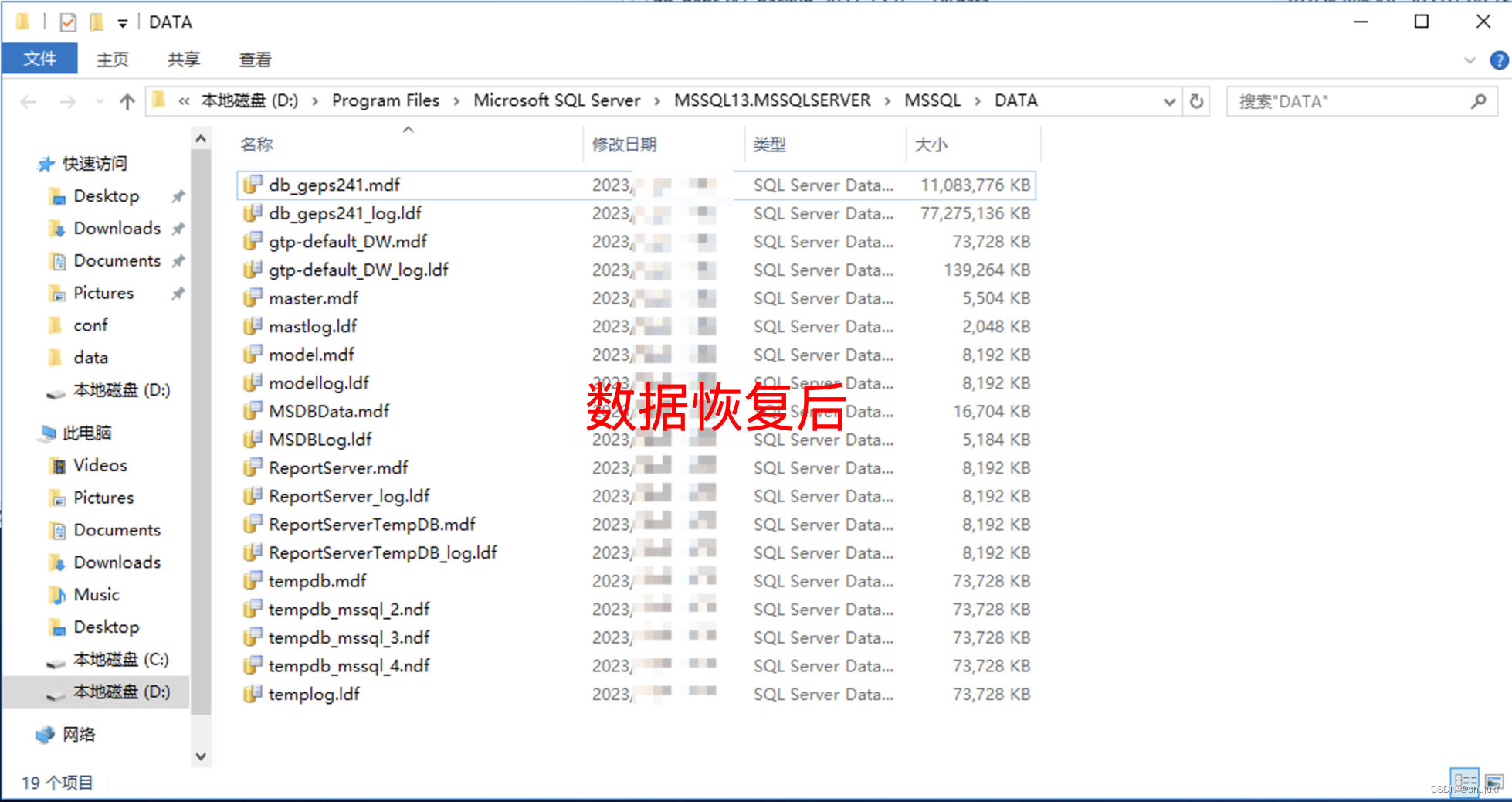
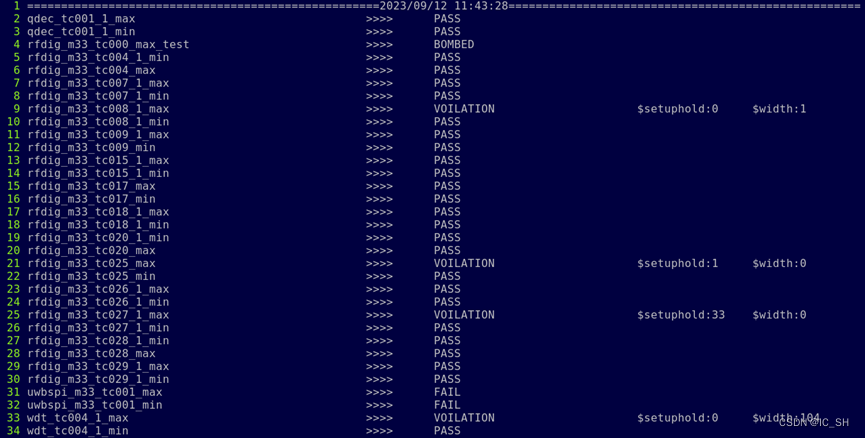
时间序列是由随时间变化的值构成,如产品销量、气温数据等等,该数据集合是个有序序列,除了数值,没有其他因素。通过对时间序列展开分析,能够回答如下问题:
- (1)被研究对象的活动特征是否有周期性(也称季节性)
- (2)被研究对象的活动特征是否有趋势性(上升或下降)
时间序列分析有多种方法,常用方法为STL(Seasonal and Trend decomposition using Loess)算法。该方法把时间序列分解为趋势项(trend component)、季节项(seasonal component)和残差项(remainder/residual component/random)的过滤过程。如下图: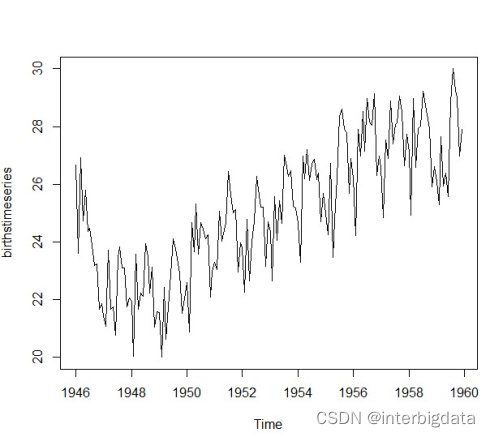

STL算法在1990年由密歇根大学的R. B. Cleveland教授以及AT&T Bell实验室的W. S. Cleveland等人研发。其特点是:
- 稳健的估计趋势项和季节项,而不会被数据中的异常行为扭曲
- 可以指定季节项的周期为采样时间间隔任意大于一的整数倍
- 可以分解有缺失值的时间序列
以下用纽约1946年1月到1959年12月的每月新生儿数作为时间序列分析人口增长的规律。代码如下:
#读入时间序列数据
import pandas as pd
X=pd.read_csv("https://robjhyndman.com/tsdldata/data/nybirths.dat",header=None,names=["birth"])
#绘制折线图
X.plot() 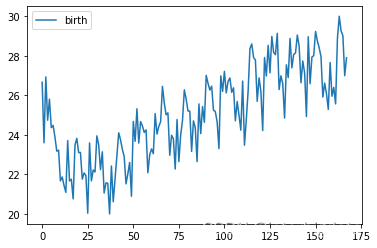
#进行时间序列分析
import statsmodels.api as sm
import matplotlib.pyplot as plt
res = sm.tsa.seasonal_decompose(X,period=12)
res.plot()
plt.xlabel("Month")
plt.show()结果如下
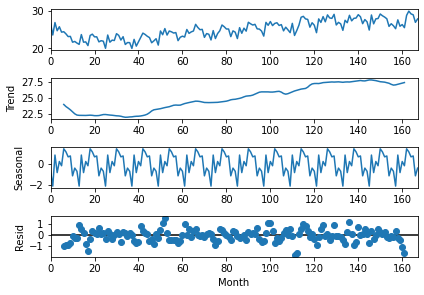
可以看人口出生在第38个月左右后出生有明显上升趋势,而且从每年3月-6期间,出生人口开始进入高峰期,从8月份左右开始出生人口急速下降,有明显季节性特征。