前言

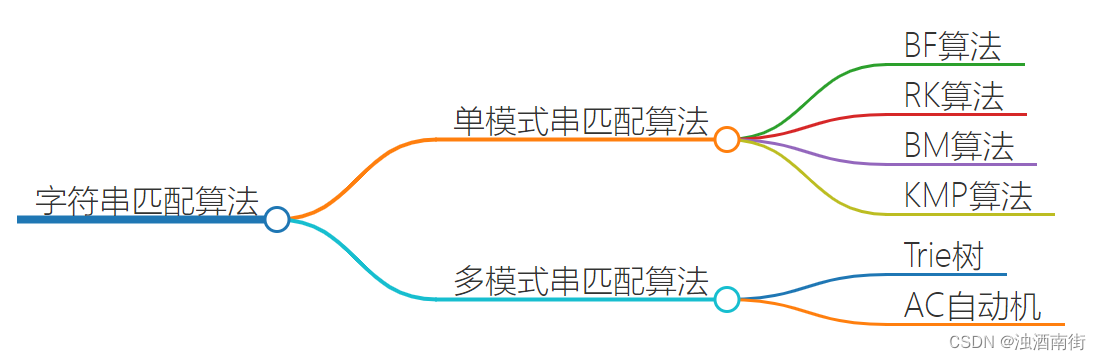
本节课程思维导图：

很多支持用户发表文本内容的网站，比如 BBS，大都会有敏感词过滤功能，用来过滤掉用户输入的一些淫秽、反动、谩骂等内容。你有没有想过，这个功能是怎么实现的呢？
实际上，这些功能最基本的原理就是字符串匹配算法，也就是通过维护一个敏感词的字典，当用户输入一段文字内容之后，通过字符串匹配算法，来查找用户输入的这段文字，是否包含敏感词。如果有，就用“***”把它替代掉。
那如何才能实现一个高性能的敏感词过滤系统呢？这就要用到今天的多模式串匹配算法。

基于单模式串和 Trie 树实现的敏感词过滤

我们前面讲的几种字符串匹配算法，有 BF 算法、RK 算法、BM 算法、KMP 算法，还有 Trie 树。前面四种算法都是单模式串匹配算法，只有 Trie 树是多模式串匹配算法。

单模式串匹配算法，是在一个模式串和一个主串之间进行匹配，也就是说，在一个主串中查找一个模式串。多模式串匹配算法，就是在多个模式串和一个主串之间做匹配，也就是说，在一个主串中查找多个模式串。

与单模式匹配算法相比，多模式匹配算法在这个问题的处理上就很高效了。它只需要扫描一遍主串，就能在主串中一次性查找多个模式串是否存在，从而大大提高匹配效率。我们知道，Trie 树就是一种多模式串匹配算法。那如何用 Trie 树实现敏感词过滤功能呢？

我们可以对敏感词字典进行预处理，构建成 Trie 树结构。这个预处理的操作只需要做一次，如果敏感词字典动态更新了，比如删除、添加了一个敏感词，那我们只需要动态更新一下 Trie 树就可以了。

当用户输入一个文本内容后，我们把用户输入的内容作为主串，从第一个字符（假设是字符 C）开始，在 Trie 树中匹配。当匹配到 Trie 树的叶子节点，或者中途遇到不匹配字符的时候，我们将主串的开始匹配位置后移一位，也就是从字符 C 的下一个字符开始，重新在 Trie 树中匹配。
借鉴单模式串的优化改进方法，能否对多模式串 Trie 树进行改进，进一步提高 Trie 树的效率呢？这就要用到 AC 自动机算法了。

经典的多模式串匹配算法：AC 自动机

AC 自动机算法，全称是 Aho-Corasick 算法。AC 自动机实际上就是在 Trie 树之上，加了类似 KMP 的 next 数组，只不过此处的 next 数组是构建在树上罢了。如果代码表示，就是下面这个样子：

public class AcNode {
  public char data; 
  public AcNode[] children = new AcNode[26]; // 字符集只包含a~z这26个字符
  public boolean isEndingChar = false; // 结尾字符为true
  public int length = -1; // 当isEndingChar=true时，记录模式串长度
  public AcNode fail; // 失败指针
  public AcNode(char data) {
    this.data = data;
  }
}

所以，AC 自动机的构建，包含两个操作：将多个模式串构建成 Trie 树；在 Trie 树上构建失败指针（相当于 KMP 中的失效函数 next 数组）。
这里我们就重点看下，构建好 Trie 树之后，如何在它之上构建失败指针？
我用一个例子给你讲解。这里有 4 个模式串，分别是 c，bc，bcd，abcd；主串是 abcd。

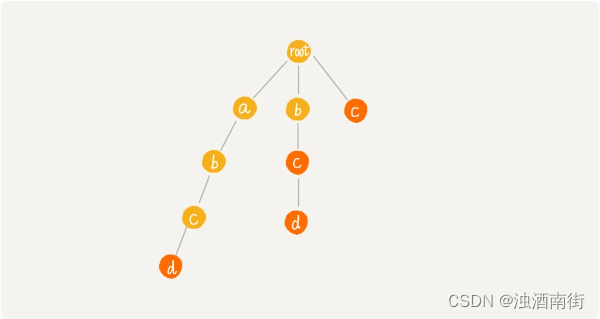
Trie 树中的每一个节点都有一个失败指针，它的作用和构建过程，跟 KMP 算法中的 next 数组极其相似。
假设我们沿 Trie 树走到 p 节点，也就是下图中的紫色节点，那 p 的失败指针就是从 root 走到紫色节点形成的字符串 abc，跟所有模式串前缀匹配的最长可匹配后缀子串，就是箭头指的 bc 模式串。
这里的最长可匹配后缀子串，我稍微解释一下。字符串 abc 的后缀子串有两个 bc，c，我们拿它们与其他模式串匹配，如果某个后缀子串可以匹配某个模式串的前缀，那我们就把这个后缀子串叫作可匹配后缀子串。
我们从可匹配后缀子串中，找出最长的一个，就是刚刚讲到的最长可匹配后缀子串。我们将 p 节点的失败指针指向那个最长匹配后缀子串对应的模式串的前缀的最后一个节点，就是下图中箭头指向的节点。

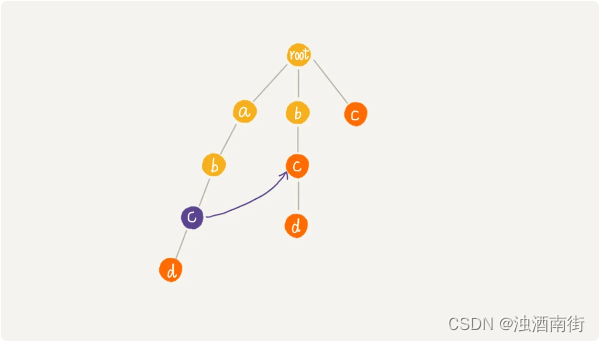
计算每个节点的失败指针这个过程看起来有些复杂。其实，如果我们把树中相同深度的节点放到同一层，那么某个节点的失败指针只有可能出现在它所在层的上一层。
当我们要求某个节点的失败指针的时候，我们通过已经求得的、深度更小的那些节点的失败指针来推导。也就是说，我们可以逐层依次来求解每个节点的失败指针。所以，失败指针的构建过程，是一个按层遍历树的过程。

首先 root 的失败指针为 NULL，也就是指向自己。当我们已经求得某个节点 p 的失败指针之后，如何寻找它的子节点的失败指针呢？我们假设节点 p 的失败指针指向节点 q，我们看节点 p 的子节点 pc 对应的字符，是否也可以在节点 q 的子节点中找到。如果找到了节点 q 的一个子节点 qc，对应的字符跟节点 pc 对应的字符相同，则将节点 pc 的失败指针指向节点 qc。

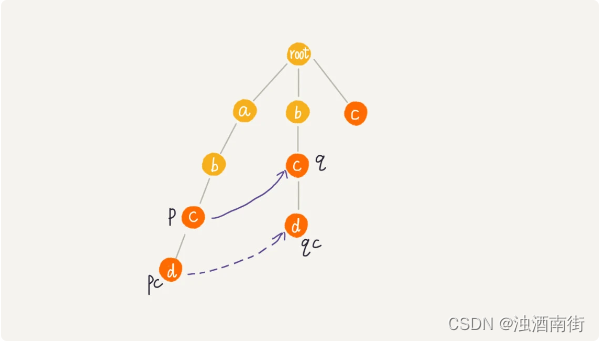
如果节点 q 中没有子节点的字符等于节点 pc 包含的字符，则令 q=q->fail（fail 表示失败指针，这里有没有很像 KMP 算法里求 next 的过程？），继续上面的查找，直到 q 是 root 为止，如果还没有找到相同字符的子节点，就让节点 pc 的失败指针指向 root。

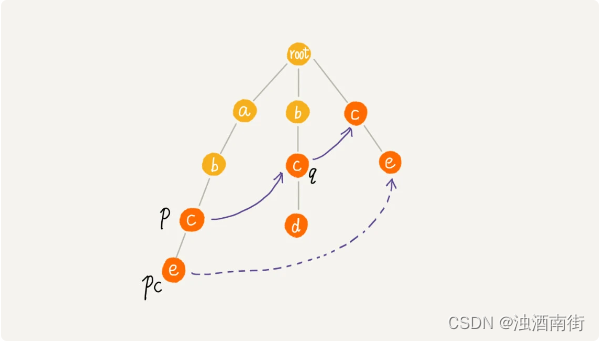
public void buildFailurePointer() {
  Queue<AcNode> queue = new LinkedList<>();
  root.fail = null;
  queue.add(root);
  while (!queue.isEmpty()) {
    AcNode p = queue.remove();
    for (int i = 0; i < 26; ++i) {
      AcNode pc = p.children[i];
      if (pc == null) continue;
      if (p == root) {
        pc.fail = root;
      } else {
        AcNode q = p.fail;
        while (q != null) {
          AcNode qc = q.children[pc.data - 'a'];
          if (qc != null) {
            pc.fail = qc;
            break;
          }
          q = q.fail;
        }
        if (q == null) {
          pc.fail = root;
        }
      }
      queue.add(pc);
    }
  }
}

通过按层来计算每个节点的子节点的失效指针，刚刚举的那个例子，最后构建完成之后的 AC 自动机就是下面这个样子：

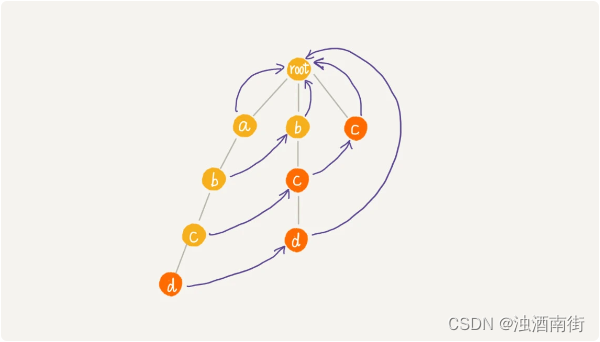
AC 自动机到此就构建完成了。我们现在来看下，如何在 AC 自动机上匹配主串？
我们还是拿之前的例子来讲解。在匹配过程中，主串从 i=0 开始，AC 自动机从指针 p=root 开始，假设模式串是 b，主串是 a。
如果 p 指向的节点有一个等于 b[i]的子节点 x，我们就更新 p 指向 x，这个时候我们需要通过失败指针，检测一系列失败指针为结尾的路径是否是模式串。这一句不好理解，你可以结合代码看。处理完之后，我们将 i 加一，继续这两个过程；如果 p 指向的节点没有等于 b[i]的子节点，那失败指针就派上用场了，我们让 p=p->fail，然后继续这 2 个过程。

public void match(char[] text) { // text是主串
  int n = text.length;
  AcNode p = root;
  for (int i = 0; i < n; ++i) {
    int idx = text[i] - 'a';
    while (p.children[idx] == null && p != root) {
      p = p.fail; // 失败指针发挥作用的地方
    }
    p = p.children[idx];
    if (p == null) p = root; // 如果没有匹配的，从root开始重新匹配
    AcNode tmp = p;
    while (tmp != root) { // 打印出可以匹配的模式串
      if (tmp.isEndingChar == true) {
        int pos = i-tmp.length+1;
        System.out.println("匹配起始下标" + pos + "; 长度" + tmp.length);
      }
      tmp = tmp.fail;
    }
  }
}

解答开篇

我这里着重讲一下，AC 自动机实现的敏感词过滤系统，是否比单模式串匹配方法更高效呢？
首先，我们需要将敏感词构建成 AC 自动机，包括构建 Trie 树以及构建失败指针。
Trie 树构建的时间复杂度是 O(mlen)，其中 len 表示敏感词的平均长度，m 表示敏感词的个数。那构建失败指针的时间复杂度是多少呢？我这里给出一个不是很紧确的上界。
假设 Trie 树中总的节点个数是 k，每个节点构建失败指针的时候，（你可以看下代码）最耗时的环节是 while 循环中的 q=q->fail，每运行一次这个语句，q 指向节点的深度都会减少 1，而树的高度最高也不会超过 len，所以每个节点构建失败指针的时间复杂度是 O(len)。整个失败指针的构建过程就是 O(klen)。
我们再来看下，用 AC 自动机做匹配的时间复杂度是多少？
跟刚刚构建失败指针的分析类似，for 循环依次遍历主串中的每个字符，for 循环内部最耗时的部分也是 while 循环，而这一部分的时间复杂度也是 O(len)，所以总的匹配的时间复杂度就是 O(n*len)。因为敏感词并不会很长，而且这个时间复杂度只是一个非常宽泛的上限，实际情况下，可能近似于 O(n)，所以 AC 自动机做敏感词过滤，性能非常高。
实际上，因为失效指针可能大部分情况下都指向 root 节点，所以绝大部分情况下，在 AC 自动机上做匹配的效率要远高于刚刚计算出的比较宽泛的时间复杂度。只有在极端情况下，如图所示，AC 自动机的性能才会退化的跟 Trie 树一样。

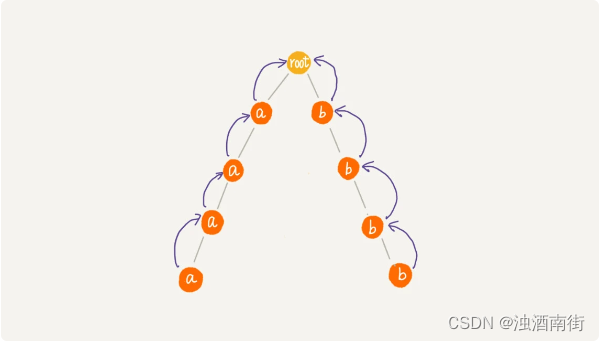
内容小结

今天我们讲了多模式串匹配算法，AC 自动机。单模式串匹配算法是为了快速在主串中查找一个模式串，而多模式串匹配算法是为了快速在主串中查找多个模式串。

AC 自动机是基于 Trie 树的一种改进算法，它跟 Trie 树的关系，就像单模式串中，KMP 算法与 BF 算法的关系一样。KMP 算法中有一个非常关键的 next 数组，类比到 AC 自动机中就是失败指针。而且，AC 自动机失败指针的构建过程，跟 KMP 算法中计算 next 数组极其相似。所以，要理解 AC 自动机，最好先掌握 KMP 算法，因为 AC 自动机其实就是 KMP 算法在多模式串上的改造。

整个 AC 自动机算法包含两个部分，第一部分是将多个模式串构建成 AC 自动机，第二部分是在 AC 自动机中匹配主串。第一部分又分为两个小的步骤，一个是将模式串构建成 Trie 树，另一个是在 Trie 树上构建失败指针。