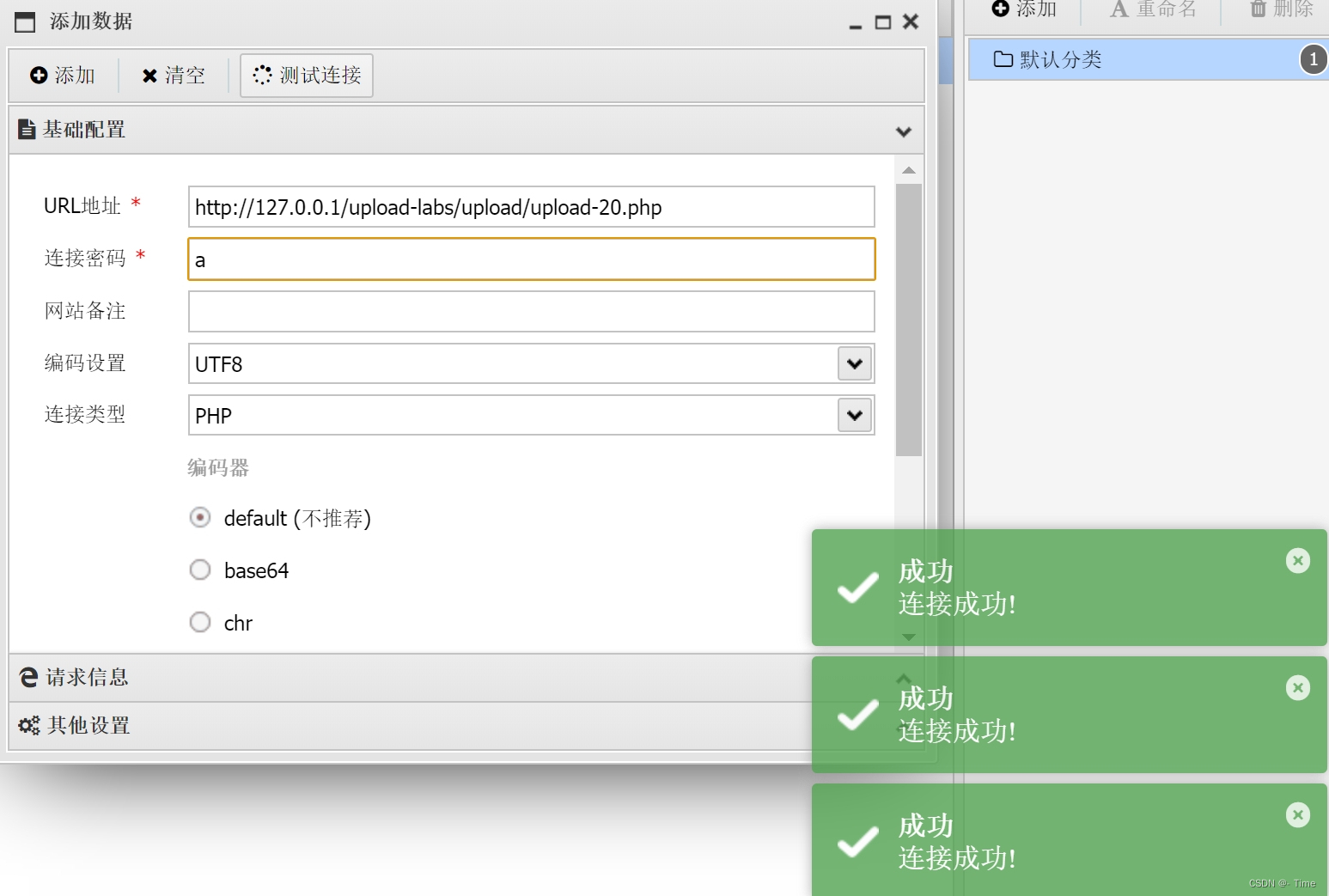
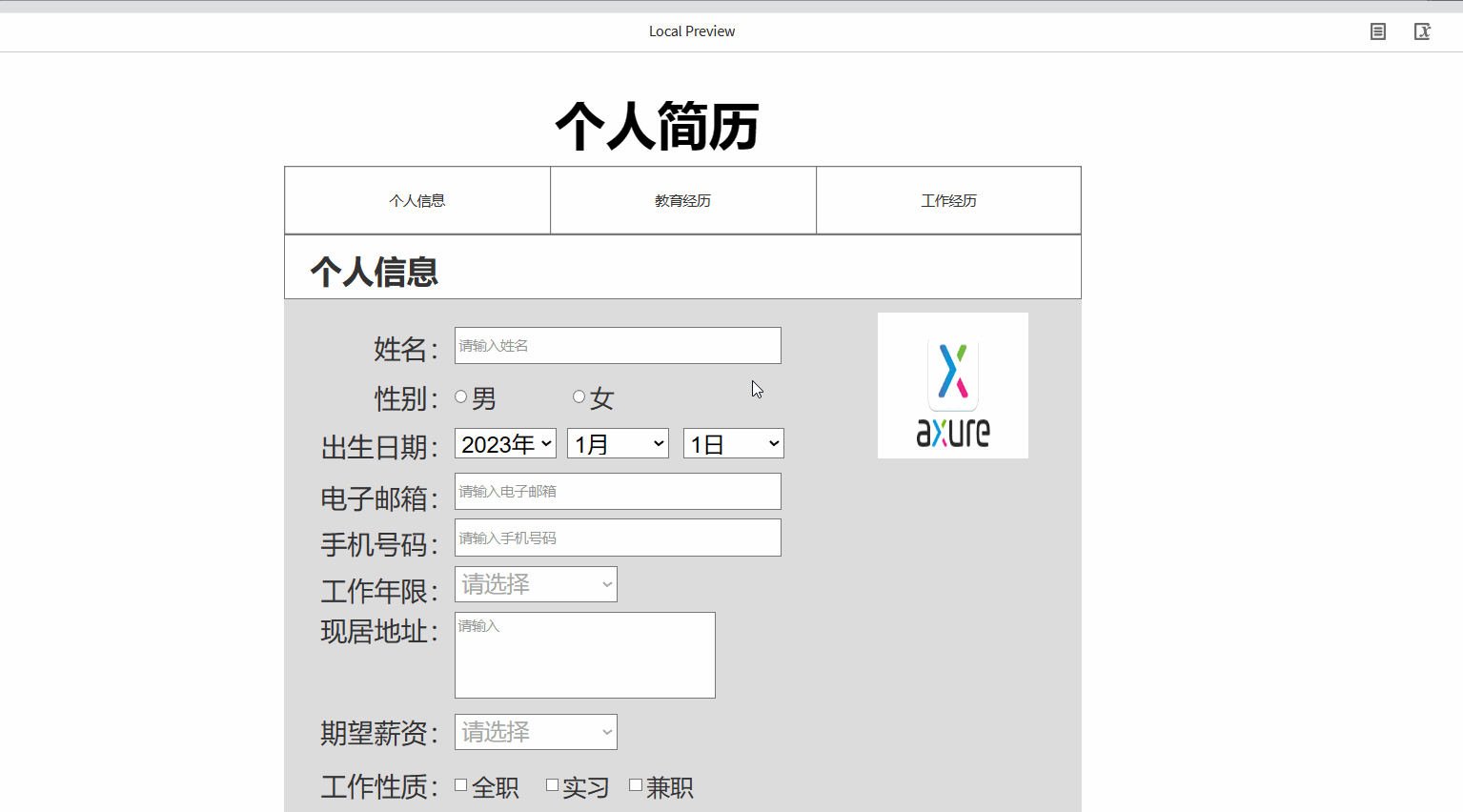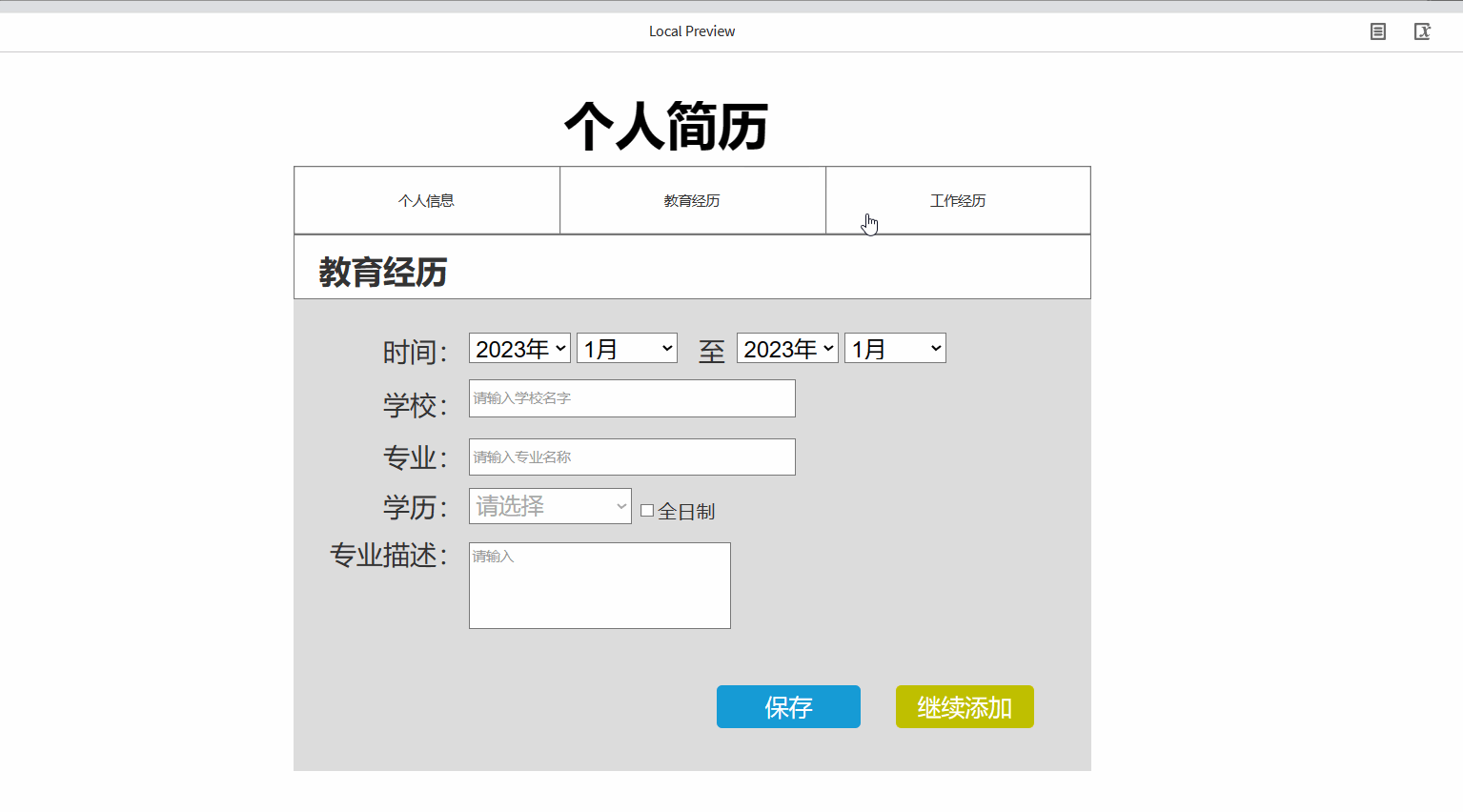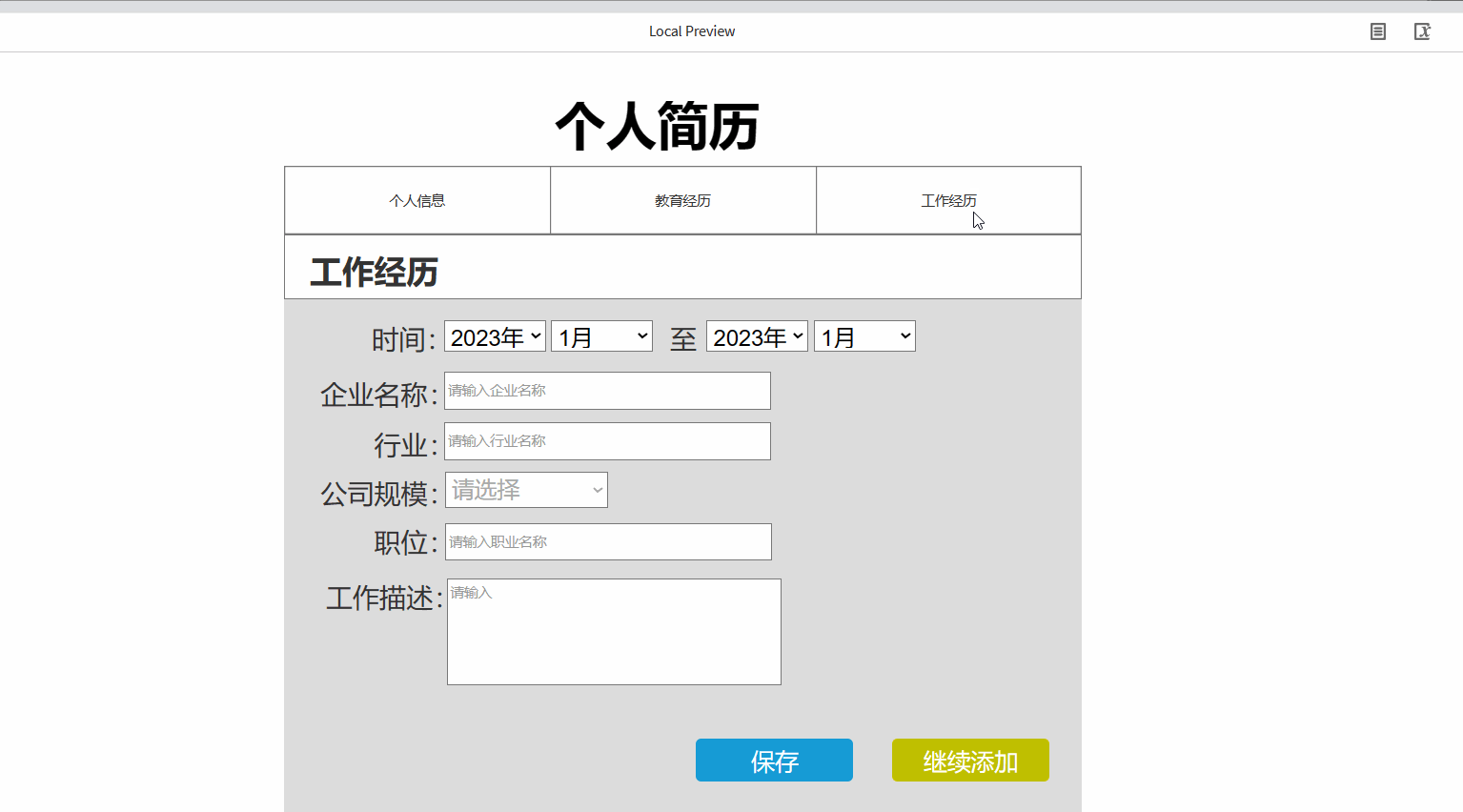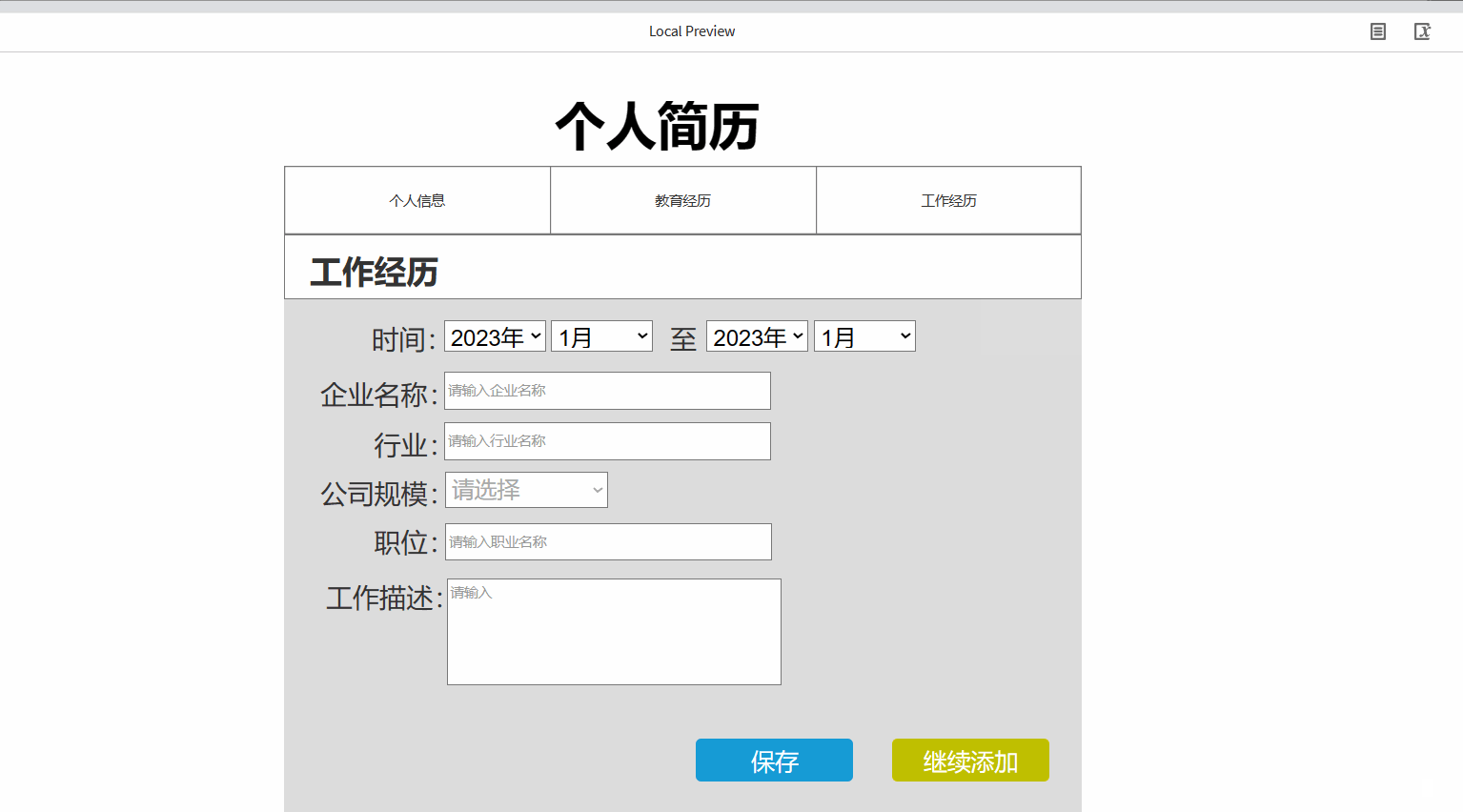
0x21 树与图的遍历

树与图最常见的储存方式就是使用一个邻接表保存它们的边集。邻接表以head数组为表头，使用ver和edge数组分别存储边的终点和权值，使用next数组模拟链表指针（就像我们在0x13节中讲解邻接表所给出的代码那样）。

1.树与图的深度优先遍历，树的DFS序、深度和重心

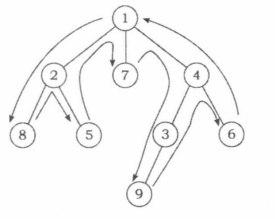
深度优先遍历，就是在每个点$x$上面对多条分支时，任意选一条边走下去，执行递归，直至回溯到点$x$后，再考虑走向其他的边，如下图所示。根据上面提到的存储方式，我们可以采用下面的代码，调用$dfs(1)$，对一张图进行深度优先遍历。

void dfs(int x)
{
    v[x]=1; //记录点x被访问过，v是visit的缩写
    for(int i=head[x];i;i=next[i])
    {
        int y=ver[i];
        if(v[y]) continue; //点y已经被访问过了
        dfs(y);
    }
}

这段代码访问每个点和每条边恰好一次（如果是无向边，正反个各访问一次），其时间复杂度为$O(N+M)$，其中$M$为边数。以这段代码为框架，我们可以统计许多关于树和图的基本信息。

时间戳

按照上述深度优先遍历的过程，以每个节点第一次被访问（$v[x]$被赋值为1时）的顺序，依次给予这$N$个节点$1\sim N$的整数标记，该标记就被称为时间戳，记为$dfn$。

例如，在上图中，$dfn[1]=1,dfn[2]=2,dfn[8]=3,dfn[5]=4,dfn[7]=5,dfn[4]=6,dfn[3]=7,dfn[9]=8,dfn[6]=9$。

树的DFS​序

一般来说，我们在对树进行深度优先遍历时，对于每个节点，在刚入递归后以及即将回溯前各记录一次该点的编号，最后产生的长度为$2N$的节点序列就称为树的$DFS$序。

树的DFS可以不使用$v$数组去记录每个点是否被访问过，而在DFS中加入这个节点的父节点，只要不遍历回父节点，就会一直向子节点遍历（利用了树每一个节点只有一个父节点）。

void dfs(int x)
{
    a[++m]=x; //a数组存储DFS序
    v[x]=1; //记录点x被访问过
    for(int i=head[x];i;i=next[i])
    {
        int y=ver[i];
        if(v[y]) continue;
        dfs(y);
	}
    a[++m]=x;
}

$DFS$序的特点是：每个节点$x$的编号在序列中恰好出现两次。设这两次出现的位置为$L[x]$和$R[x]$，那么闭区间$[L[x],R[x]]$就是以$x$为根的子树的$DFS$序。这使我们在很多树相关的问题中，可以通过$DFS$序把子树统计转化为序列上的区间统计。

另外，二叉树的先序、中序与后序遍历序列，也就是通过深度优先遍历产生的，大多数程序设计入门级的书籍上都有详细讲解，在此就不再赘述。读者应该掌握这几种遍历，以及它们之间的联系与转化。

树的深度（自顶而下统计）

树中各个节点的深度是一种自顶而下的统计信息。起初，我们已知根节点的深度为0。若节点$x$的深度为$d[x]$，则它的子节点$y$的深度就是$d[y]=d[x]+1$。在深度优先遍历的过程中结合自顶而下的递推，就可以求出每个节点的深度$d$。

void dfs(int x)
{
    v[x]=1;
    for(int i=head[x];i;i=next[i])
    {
        int y=ver[i];
        if(v[y]) continue;
        d[y]=d[x]+1;
        dfs(y);
    }
}

树的重心（自底而上统计）

当然，也有很多信息是自底而上进行统计的，比如以每个节点$x$为根的子树大小$size[x]$。对于叶子节点，我们已知“以它为根的子树”大小为1。若节点$x$有$k$个子节点$y_1\sim y_k$，并且以$y_1\sim y_k$为根的子树大小分别是$size[y_1],size[y_2],...,size[y_k]$，则以$x$为根的子树的大小就是$size[x]=size[y_1]+size[y_2]+...+size[y_k]+1$。

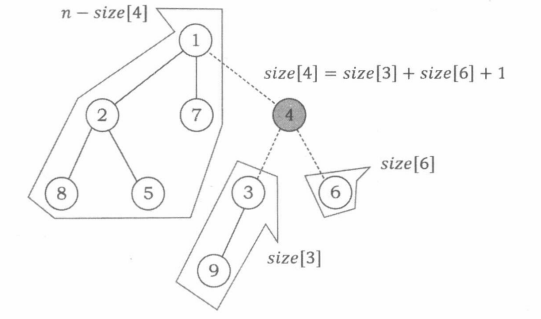
对于一个节点$x$，如果我们把它从树中删除，那么原来的一棵树可能就会分成若干个不相连的的部分，其中每一部分都是一棵子树。设$max\_part(x)$表示在删除节点$x$后产生的子树中，最大的一棵的大小。使$max\_part$函数取到最小值的节点$p$就被称为整棵树的重心。例如上图数的重心应该是节点1。通过下面的代码，我们可以统计出$size$数组，并求出树的重心。

void dfs(int x)
{
    v[x]=1;size[x]=1; //子树的大小
    int max_part=0;   //删掉x后分成的最大子树的大小
    for(int i=head[x];i;i=next[i])
    {
        int y=ver[i];
        if(v[y]) continue;
        dfs(y);
        size[x]+=size[y]; //从子节点向父节点递推
        max_part=max(max_part,size[y]);
    }
    max_part=max(max_part,n-size[x]); //n为整棵树的节点数目
    if(max_part<ans)
    {
        ans=max_part; //全局变量ans记录重心对应的max_part值
        pos=x;        //全局变量pos记录重心
    }    
}

图的连通块划分

上面的代码每从$x$开始一次遍历，就会访问$x$能够到达的所有的点与边。因此，通过多次深度优先遍历，可以划分出一张无向图中的各个连通块。同理，对于一个森林进行深度优先遍历，可以划分出森林中的每棵树。如下面的代码所示，$cnt$就是无向图包含的连通块的个数，$v$数组标记了每个点属于哪个连通块。

void dfs(int x)
{
    v[x]=cnt;
    for(int i=head[x];i;i=next[i])
    {
        int y=ver[i];
        if(v[y]) continue;
        dfs(y);
    }
}
for(int i=1;i<=n;++i) //在int main()中
{
    if(!v[i])
    {
        cnt++;
        dfs(i);
    }
}

2.树与图的广度优先遍历，拓扑排序

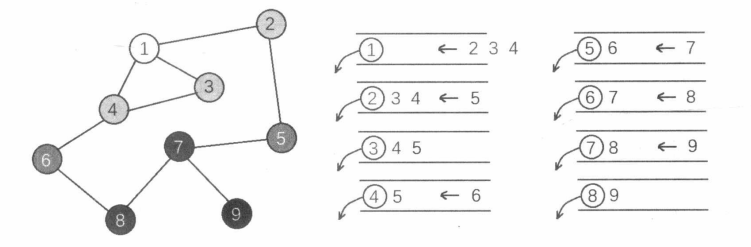
树与图的广度优先遍历需要使用一个队列来实现。起初，队列中仅包含一个起点（例如1号节点）。在广度优先遍历的过程中，我们不断从队头取出一个节点$x$，对于$x$面对的多条分支，把沿着每条分支到达的下一个节点（如果尚未访问过）插入队尾。重复执行上述过程直到队列为空。

我们可以采用下面的代码对一张图进行广度优先遍历（关于代码中的$STLqueue$，参见0x71节）。

void bfs()
{
    memset(d,0,sizeof(d));
    queue<int> q;
    q.push(1);
    d[1]=1;
    while(!q.empty())
    {
        int x=q.front();
        q.pop();
        for(int i=head[x];i;i=next[i])
        {
            int y=ver[i];
            if(d[y]) continue;
            d[y]=d[x]+1;
            q.push(y);
        }
    }
}

在上面的代码中，我们在广度优先遍历的过程中顺便求出了一个$d$数组。对于一棵树来讲，$d[x]$就是点$x$在树中的深度。对于一张图来讲，$d[x]$被称为点$x$的层次（从起点1走到点$x$需要经过的最少点数）。从代码和示意图中我们可以发现，广度优先遍历是一种按照层次顺序进行访问的方法，它具有如下两个重要性质：

1.在访问完所有的第$i$层节点后，才会开始访问第$i+1$层节点。

2.任意时刻，队列中至多有两个层次的节点。若其中一部分节点属于第$i$层，则另一部分节点属于$i+1$层，并且所有第$i$层节点排在第$i+1$层节点之前。也就是说，广度优先遍历队列中的元素关于层次满足“两段性”和“单调性”。

这两条性质是所有广度优先思想的基础。我们在0x26节的“广搜变形”中会再次提及并探讨。与深度优先遍历一样，上面这段代码的时间复杂度也是$O(N+M)$。

拓扑排序

给定一张有向无环图，若一个由图中所有点构成的序列$A$满足：对于图中的每条边$(x,y)$，$x$在$A$中都出现在$y$之前，则称$A$是该有向无环图定点的一个拓扑序。求解序列$A$的过程就称为拓扑排序。

拓扑排序过程的思想非常简单，我们只需要不断选择图中入度为0的节点$x$，然后把$x$连向的点的入度减1。我们可以结合广度优先遍历的框架来高效地实现这个过程：

1.建立空的拓扑序列$A$。

2.预处理出所有点的入度$deg[i]$，起初把所有入度为0的点入队。

3.取出队头节点$x$，把$x$加入拓扑排序的$A$的末尾。

4.对于从$x$出发的每条边$(x,y)$，把$deg[y]$减1。若被减为0，则把$y$入队。

5.重复第$3\sim 4$步知道队列为空，此时$A$即为所求。

拓扑排序可以判定有向图中是否存在环。我们可以对任意有向图执行上述过程，在完成后检查$A$序列的长度。若$A$序列的长度小于图中点的数量，则说明某些节点未被遍历，进而说明图中有环。读者可以参考下面的程序，画图模拟拓扑排序算法。

void add(int x,int y)
{
    ver[++tot]=y,next[tot]=head[x],head[x]=tot;
    deg[y]++;
}
void topsort()
{
    queue<int> q;
    for(int i=1;i<=n;++i)
        if(deg[i]==0) q.push(i);
   	while(!q.empty())
    {
        int x=q.front();
        q.pop();
        a[++cnt]=x;
        for(int i=head[x];i;i=next[i])
        {
            int y=ver[i];
            if(--deg[y]==0) q.push(y);
		}
    }
}
int main()
{
    cin>>n>>m;
    for(int i=1;i<=m;++i)
    {
        int x,y;
        scanf("%d%d",&x,&y);
        add(x,y);
	}
    topsort();
    for(int i=1;i<=cnt;++i)
        printf("%d ",a[i]);
   	cout<<endl;
}