文章目录
- 一、强化学习问题
- 1、交互的对象
- 2、强化学习的基本要素
- 3、策略(Policy)
- 4、马尔可夫决策过程
- 5、强化学习的目标函数
- 6、值函数
- 1. 状态值函数(State Value Function)
- a. 状态值函数的定义
- b. 贝尔曼方程(Bellman Equation)
- 2. 状态-动作值函数(State-Action Value Function)
- 3. 值函数的作用
- a. 评估策略
- b. 优化策略
- c. 改进策略
- d. 探索与利用的平衡
一、强化学习问题
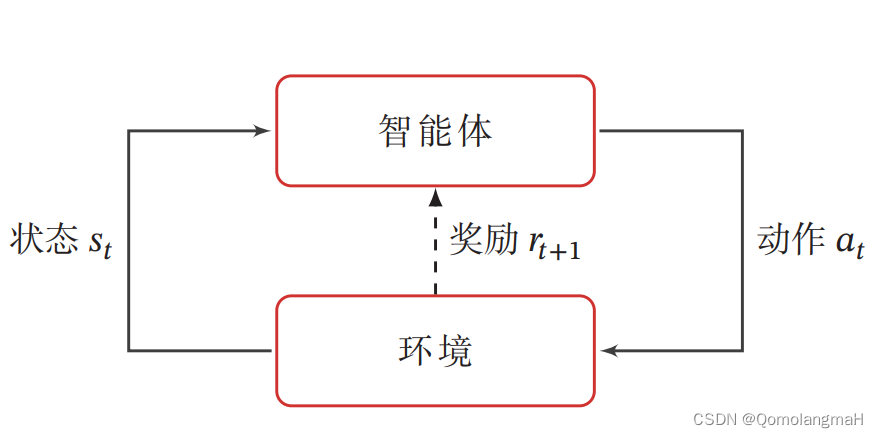
强化学习的基本任务是通过智能体与环境的交互学习一个策略,使得智能体能够在不同的状态下做出最优的动作,以最大化累积奖励。这种学习过程涉及到智能体根据当前状态选择动作,环境根据智能体的动作转移状态,并提供即时奖励的循环过程。
1、交互的对象
在强化学习中,有两个可以进行交互的对象:智能体和环境
-
智能体(Agent):能感知外部环境的状态(State)和获得的奖励(Reward),并做出决策(Action)。智能体的决策和学习功能使其能够根据状态选择不同的动作,学习通过获得的奖励来调整策略。
-
环境(Environment):是智能体外部的所有事物,对智能体的动作做出响应,改变状态,并反馈相应的奖励。
2、强化学习的基本要素
强化学习涉及到智能体与环境的交互,其基本要素包括状态、动作、策略、状态转移概率和即时奖励。
-
状态(State):对环境的描述,可能是离散或连续的。
-
动作(Action):智能体的行为,也可以是离散或连续的。
-
策略(Policy):智能体根据当前状态选择动作的概率分布。
-
状态转移概率(State Transition Probability):在给定状态和动作的情况下,环境转移到下一个状态的概率。
-
即时奖励(Immediate Reward):智能体在执行动作后,环境反馈的奖励。
3、策略(Policy)
策略(Policy)就是智能体如何根据环境状态 𝑠 来决定下一步的动作 𝑎(智能体在特定状态下选择动作的规则或分布)。
- 确定性策略(Deterministic Policy) 直接指定智能体应该采取的具体动作
- 随机性策略(Stochastic Policy) 则考虑了动作的概率分布,增加了对不同动作的探索。
上述概念可详细参照:【深度学习】强化学习(一)强化学习定义
4、马尔可夫决策过程
为了简化描述,将智能体与环境的交互看作离散的时间序列。智能体从感知到的初始环境 s 0 s_0 s0 开始,然后决定做一个相应的动作 a 0 a_0 a0,环境相应地发生改变到新的状态 s 1 s_1 s1,并反馈给智能体一个即时奖励 r 1 r_1 r1,然后智能体又根据状态 s 1 s_1 s1做一个动作 a 1 a_1 a1,环境相应改变为 s 2 s_2 s2,并反馈奖励 r 2 r_2 r2。这样的交互可以一直进行下去: s 0 , a 0 , s 1 , r 1 , a 1 , … , s t − 1 , r t − 1 , a t − 1 , s t , r t , … , s_0, a_0, s_1, r_1, a_1, \ldots, s_{t-1}, r_{t-1}, a_{t-1}, s_t, r_t, \ldots, s0,a0,s1,r1,a1,…,st−1,rt−1,at−1,st,rt,…,其中 r t = r ( s t − 1 , a t − 1 , s t ) r_t = r(s_{t-1}, a_{t-1}, s_t) rt=r(st−1,at−1,st) 是第 t t t 时刻的即时奖励。这个交互过程可以被视为一个马尔可夫决策过程(Markov Decision Process,MDP)。
关于马尔可夫决策过程可详细参照:【深度学习】强化学习(二)马尔可夫决策过程
5、强化学习的目标函数
强化学习的目标是通过学习一个良好的策略来使智能体在与环境的交互中获得尽可能多的平均回报。强化学习的目标函数 J ( θ ) J(\theta) J(θ) 定义如下: J ( θ ) = E τ ∼ p θ ( τ ) [ G ( τ ) ] = E τ ∼ p θ ( τ ) [ ∑ t = 0 T − 1 γ t r t + 1 ] J(\theta) = \mathbb{E}_{\tau \sim p_{\theta}(\tau)}[G(\tau)] = \mathbb{E}_{\tau \sim p_{\theta}(\tau)}\left[\sum_{t=0}^{T-1} \gamma^t r_{t+1}\right] J(θ)=Eτ∼pθ(τ)[G(τ)]=Eτ∼pθ(τ)[t=0∑T−1γtrt+1]其中, θ \theta θ 表示策略函数的参数, τ \tau τ 表示强化学习的轨迹, γ \gamma γ 是折扣率……
- 这个目标函数表达的是在策略 π θ \pi_{\theta} πθ 下,智能体与环境交互得到的总回报的期望。(这个期望是对所有可能的轨迹进行的)
- 总回报(Total Return)是对一个轨迹的累积奖励,引入折扣率(Discount Factor)来平衡短期和长期回报。
- 总回报:对于一次交互过程的轨迹,总回报是累积奖励的和。
- 折扣回报:引入折扣率,考虑未来奖励的权重。
关于目标函数可详细参照:【深度学习】强化学习(三)强化学习的目标函数
6、值函数
在强化学习中,为了评估策略 π \pi π 的期望回报,引入了值函数的概念,包括状态值函数和状态-动作值函数。
1. 状态值函数(State Value Function)
a. 状态值函数的定义
状态值函数表示从某个状态开始,按照特定策略执行后获得的期望总回报。
- 状态值函数的定义:
V π ( s ) = E τ ∼ p ( τ ) [ ∑ t = 0 T − 1 γ t r t + 1 ∣ τ s 0 = s ] V^\pi(s) = \mathbb{E}_{\tau \sim p(\tau)} \left[ \sum_{t=0}^{T-1} \gamma^t r_{t+1} \bigg| \tau_{s_0} = s \right] Vπ(s)=Eτ∼p(τ)[t=0∑T−1γtrt+1 τs0=s]
其中, τ \tau τ 表示强化学习的轨迹, γ \gamma γ 是折扣因子, s s s 是状态。状态值函数 V π ( s ) V^\pi(s) Vπ(s) 表示从状态 s s s 开始,执行策略 π \pi π 后获得的期望总回报。
b. 贝尔曼方程(Bellman Equation)
进一步,我们可以使用贝尔曼方程来表示状态值函数的计算:
V π ( s ) = E a ∼ π ( a ∣ s ) [ E s ′ ∼ p ( s ′ ∣ s , a ) [ r ( s , a , s ′ ) + γ V π ( s ′ ) ] ] V^\pi(s) = \mathbb{E}_{a \sim \pi(a|s)} \left[ \mathbb{E}_{s' \sim p(s'|s,a)} \left[ r(s, a, s') + \gamma V^\pi(s') \right] \right] Vπ(s)=Ea∼π(a∣s)[Es′∼p(s′∣s,a)[r(s,a,s′)+γVπ(s′)]]
-
推导过程

-
贝尔曼方程表明,当前状态的值函数可以通过下一个状态的值函数来计算,这是强化学习中常用的迭代计算方法之一。在实际应用中,通过不断更新状态值函数,智能体可以逐步优化其策略,从而在环境中获得更好的回报。
2. 状态-动作值函数(State-Action Value Function)
状态-动作值函数(Q函数或Q值)是另一种重要的值函数,它衡量在给定状态 s s s 下,采取特定动作 a a a 并按照某一策略执行后所获得的期望总回报。
-
状态-动作值函数的定义:
Q π ( s , a ) = E s ′ ∼ p ( s ′ ∣ s , a ) [ r ( s , a , s ′ ) + γ V π ( s ′ ) ] Q^\pi(s, a) = \mathbb{E}_{s' \sim p(s'|s,a)} \left[ r(s, a, s') + \gamma V^\pi(s') \right] Qπ(s,a)=Es′∼p(s′∣s,a)[r(s,a,s′)+γVπ(s′)]其中, Q π ( s , a ) Q^\pi(s, a) Qπ(s,a) 表示在状态 s s s 下采取动作 a a a 后,按照策略 π \pi π 执行的期望总回报。 -
这个定义使用了之前介绍的状态值函数 V π ( s ) V^\pi(s) Vπ(s),表示了当前状态-动作对的价值。
-
状态值函数和状态-动作值函数之间的关系可以通过以下方程表示: V π ( s ) = E a ∼ π ( a ∣ s ) [ Q π ( s , a ) ] V^\pi(s) = \mathbb{E}_{a \sim \pi(a|s)} \left[ Q^\pi(s, a) \right] Vπ(s)=Ea∼π(a∣s)[Qπ(s,a)]
- 这说明状态值函数是关于动作的期望值,而状态-动作值函数则提供了每个动作在给定状态下的具体估计值。
-
状态-动作值函数满足贝尔曼方程,表示为:
Q π ( s , a ) = E s ′ ∼ p ( s ′ ∣ s , a ) [ r ( s , a , s ′ ) + γ E a ′ ∼ π ( a ′ ∣ s ′ ) [ Q π ( s ′ , a ′ ) ] ] Q^\pi(s, a) = \mathbb{E}_{s' \sim p(s'|s,a)} \left[ r(s, a, s') + \gamma \mathbb{E}_{a' \sim \pi(a'|s')} \left[ Q^\pi(s', a') \right] \right] Qπ(s,a)=Es′∼p(s′∣s,a)[r(s,a,s′)+γEa′∼π(a′∣s′)[Qπ(s′,a′)]] -
Q函数的不断迭代计算可以帮助智能体更好地理解状态和动作的关联,从而制定更优化的策略。在深度强化学习中,Q函数的使用更为普遍,特别是在处理复杂、连续状态和动作空间的问题时。
3. 值函数的作用
值函数的引入为强化学习提供了一种有效的手段,使得我们可以通过对值函数的优化来改进策略,从而使智能体更好地在环境中行动。
-
状态值函数 V π ( s ) V^{\pi}(s) Vπ(s)
- 评估在状态 s s s 下采用策略 π \pi π 的效果,即从状态 s s s 出发,执行策略 π \pi π 所获得的期望总回报。
- 可以用来比较不同状态的价值,帮助智能体决策。
-
状态-动作值函数 Q π ( s , a ) Q^{\pi}(s, a) Qπ(s,a):
- 评估在状态 s s s 下采取动作 a a a 并执行策略 π \pi π 的效果,即获得的期望总回报。
- 可以用来指导智能体在给定状态下选择最优动作。
a. 评估策略
值函数可以用于评估给定策略的好坏:比如,状态值函数
V
π
(
s
)
V^\pi(s)
Vπ(s) 表示在策略
π
\pi
π 下,从状态
s
s
s 开始执行策略的期望总回报,通过评估状态值函数,我们可以了解在不同状态下策略的性能,并比较不同策略之间的优劣。
V
π
(
s
)
=
E
τ
∼
π
[
G
(
τ
)
∣
τ
0
=
s
]
V^\pi(s) = \mathbb{E}_{\tau \sim \pi} \left[ G(\tau) \mid \tau_0 = s \right]
Vπ(s)=Eτ∼π[G(τ)∣τ0=s]
b. 优化策略
基于值函数,我们可以通过优化策略来提高智能体的性能:当我们在某个状态 s s s 发现一个动作 a ∗ a^* a∗ 使得 Q π ( s , a ∗ ) > V π ( s ) Q^\pi(s, a^*) > V^\pi(s) Qπ(s,a∗)>Vπ(s),即执行动作 a ∗ a^* a∗ 的回报比当前策略的状态值更高,我们可以调整策略的参数,增加在状态 s s s 选择动作 a ∗ a^* a∗ 的概率,从而优化策略。
π
′
(
a
∣
s
)
=
{
π
(
a
∣
s
)
+
ϵ
if
a
=
a
∗
π
(
a
∣
s
)
−
ϵ
if
a
≠
a
∗
\pi'(a|s) = \begin{cases} \pi(a|s) + \epsilon & \text{if } a = a^* \\ \pi(a|s) - \epsilon & \text{if } a \neq a^* \end{cases}
π′(a∣s)={π(a∣s)+ϵπ(a∣s)−ϵif a=a∗if a=a∗
这个过程可以通过各种优化算法实现,例如梯度上升法(Policy Gradient Methods)。
c. 改进策略
通过值函数的指导,我们可以设计更智能的策略,不仅考虑当前状态的回报,还能充分考虑长期的影响。
d. 探索与利用的平衡
通过对值函数的估计,智能体可以更好地判断哪些动作可能导致更高的回报,从而在探索新动作和利用已知好动作之间找到平衡。
值函数在强化学习中起到了桥梁的作用,连接了策略、状态和动作的关系。它们是智能体学习和改进的核心工具,使其能够在未知环境中获得最大的累积奖励。在深度强化学习中,利用深度神经网络逼近值函数,使其能够应对更复杂的状态和动作空间。