论文：Linformer: Self-Attention with Linear Complexity
作者：Sinong Wang, Belinda Z. Li, Madian Khabsa, Han Fang, Hao Ma
时间：2020

模型结构较于简单，证明有点难，有时间可以做一下文章的证明分析；

一、完整代码

这里我们使用python代码进行实现

# 完整代码在这里
# 模型结构较于简单，有时间再弄

二、论文解读

2.1 介绍

这是一篇介绍transformer的优化模型的论文，其对普通的transformer模型进行了优化，把时间复杂度和空间复杂度都从$O(n^2)$降低为了$O(n)$；论文推出的模型叫Linformer，其主要思想利用到了两个思想，一个是the distributional Johnson–Lindenstrauss lemma, the Eckart–Young–Mirsky Theorem；这两个思想一同证实了利用降维去构造一个低秩矩阵来降低复杂度的可行性；

为什么要改进transformer模型：计算量太大，价格昂贵，操作复杂度为$O(n^2)$；部署困难，并不容易进行推理；

目前的其他降维方法：Sparse transformer利用Sparse matrix；Reformer利用locally-sensitive hashing (LSH)，并且只有序列长度大于2048的时候才有用；

不同模型架构方法对比如下：

相比于图中的模型，Linformer在复杂度和操作上是最佳的；

在这里提一下Transformer的自注意力机制，这都是非常基础了；

提高transformer的效率有很多种办法，下面简单介绍几种：

Mixed Precision：使用半精度或混合精度表示，即采用量化的方式加快计算；

Knowledge Distillation：和DistillBERT一样，利用学生模型去学习教师模型的分布预测；

Sparse Attention：只计算对角线部分的注意力权重；

该技术通过在上下文映射矩阵P中添加稀疏性来提高自我注意的效率。例如，sparse transformer只计算矩阵P的对角线附近的Pij（而不是所有的Pij）。同时，block-wise self-attention将P划分为多个块，只计算所选块内的Pij。然而，这些技术也遭受了很大的性能下降，同时只有有限的额外加速，即下降2%，加速20%。

LSH Attention：操作复杂，有效果但是有限制；

Locally-sensitive hashing（LSH）注意在计算点积注意时采用了多轮哈希方案，在理论上将自注意复杂度降低到O（n log(n)）。然而，在实践中，它们的复杂度项有一个很大的常数1282，并且只有当序列长度非常长时，它才比普通的变压器更有效。

Improving Optimizer Efficiency：没注意过，不出名；

Microbatching将一批分成小的微批（可以放入内存），然后通过梯度积累分别向前和向后运行。Gradient checkpointing仅通过缓存一个图层子集的激活来节省内存。在从最新的检查点进行反向传播期间，将重新计算未缓存的激活。这两种技术都可以利用时间来换取内存，而且都不能加快推理的速度。

2.2 Self-Attention is Low Rank

如标题，这节主要证明了self-attention其实是一个低秩矩阵；

作者使用了两个预训练的transformer模型，RoBERTa-base和RoBERTa-large，前者是12层的模型，后者是24层的模型；

作者通过对每一层的特征值进行分解，然后做图如下，纵坐标代表归一化的累积特征值，由于序列长度是512维的，所以一个有512个特征值；

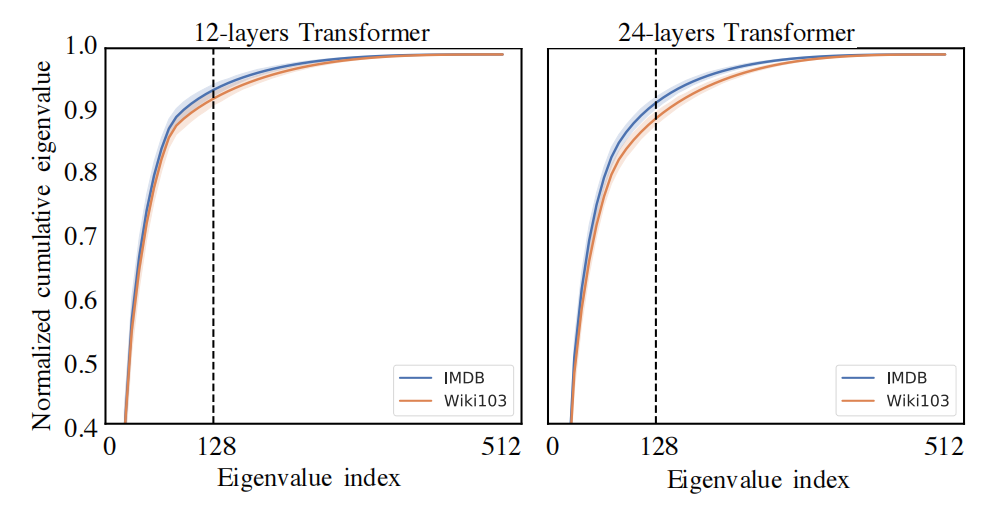
通过观察发现，当取前面128个较大的特征值时，累积特征值已经到达了95%，通过主成分可以直到，前面128个较大的特征值可以表示整体的95%的信息，所以我们可以对其使用奇异值分解的方式降低维度从而达到降低复杂度的目的；

下图是不同层次的累积贡献度的谱分布，如下：

从上图中我们可以发现：高层的谱分布比下层更倾斜，这意味着在高层，更多的信息集中在最大奇异值，导致了P的秩相较于底层较低；

这里利用两个思想，一个是the distributional Johnson–Lindenstrauss lemma, the Eckart–Young–Mirsky Theorem；前者证明出现高维矩阵是低秩矩阵这种现象是正常的，后者表示奇异值分解在相同的维度下获得低秩矩阵的绝大部分信息；而奇异值分解是相当需要计算量的，高维矩阵分解操作起来很复杂，这里论文中使用投影的方式解决了这一问题；

2.3 模型架构

直接看下面这张图，就知道作者做了什么处理：

在Linear层得到了$Q,K,V$后，为了降低$K,V$的维度，其使用了投影到低维的方式，具体公式如下：

之前$QW,KW,VW$都是一个n·d_model的矩阵，在这里有$E_i,F_i$都是一个k·n的矩阵，有前面的softmax变成了一个 n·k的矩阵，后者是一个k·d的矩阵，这里的空间复杂度为$O(kn+2kd)$，把平方项降低为一次项；如果我们可以选择一个非常小的投影维数k，即kn，那么我们就可以显著地减少内存和空间消耗；

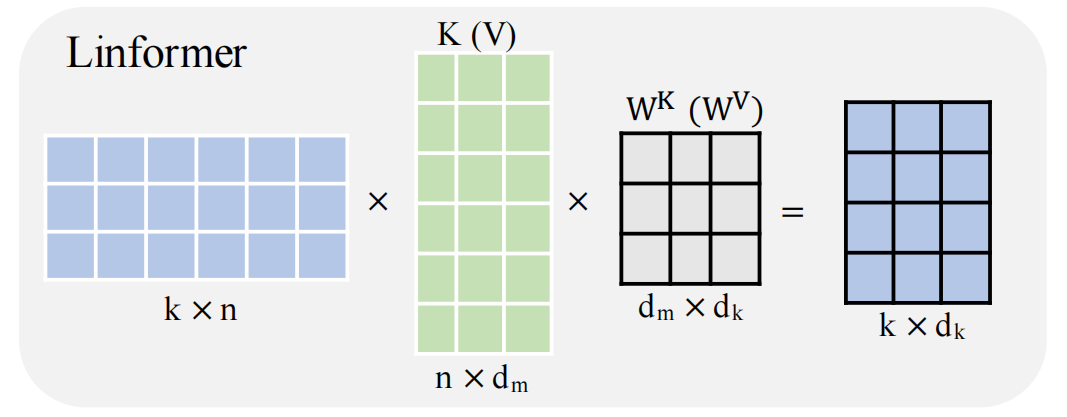
从下图，我们可以发现设置的k越小，推理速度越快；

这和预期一致；

继续优化可以采用方法：

Parameter sharing between projections:即共享投影层的参数，

• 头之间共享：在每一层中的投影矩阵$E,F$中，我们共享两个投影矩阵$E_i$和$F_i$，确保在每一个头$i$中，有$E_i=E,F_i=F$；
• $K,V$之间共享：在每一层中的投影矩阵$E,F$中，我们共享两个投影矩阵$E_i$和$F_i$并化为一个矩阵，确保在每一个头$i$中，有$E_i=F_i=E$；
• 层与层之间共享：在所有的层中，对于所有的头部，对于所有的键和值，都使用一个投影矩阵$E$；

Nonuniform projected dimension:不均匀投影，意思是结合不同层的低秩矩阵的秩，如上文我们可以得到高层的秩要比底层的秩要小，所以我们可以在高层设置较小的k在低层设置较大的k；

General projections: 我们可以采用其他的机制来缩小维度，而不是利用一个简单的投影的方式，例如均值池化，最大池化，卷积等等方式来缩小维度代替简单投影；

2.4 结果

论文中的结果可视化如下：

接下来对结果做一些解释：

a,b两图作者做了ppl曲线来判断模型的效果，在$n=512$时，随着k的增加，模型越来越贴近standard transformer曲线，有的模型甚至超过了；在$n=1024$时，表现了相同的趋势，但是同时可以发现，效果是非常贴近于标准模型的；

c图中，使用了三种参数共享策略来检验模型结果，可以发现参数共享并不会产生较大的影响，所以我们可以在模型中使用参数贡献，在保存相同的效果下，减少模型的参数；

d图中随着序列长度的增加，投影维数保持不变，收敛后的最终ppl仍然保持大致相同。而且不同曲线之间的间隔大小似乎相等，说明这是线性的；

下游任务模型效果，可以发现模型效果有些甚至超过了BERT和DistillBERT；

从模型$n=1024，k=256$和模型$n=512，k=256$效果一致可以看出来，模型的效果由预测维度k而不是比率n/k决定；

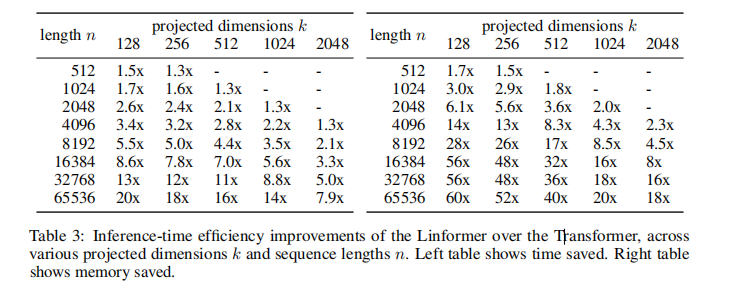
这是推理时间效果和空间复杂度效果的对比，可以看到Linformer可以在保持效果的情况下，大大优化时间和空间复杂度；

三、整体总结

这是一篇介绍transformer的优化模型的论文，其对普通的transformer模型进行了优化，把时间复杂度和空间复杂度都从$O(n^2)$降低为了$O(n)$；论文推出的模型叫Linformer，其主要思想利用到了两个思想，一个是the distributional Johnson–Lindenstrauss lemma, the Eckart–Young–Mirsky Theorem；这两个思想一同证实了利用降维去构造一个低秩矩阵来降低复杂度的可行性；