最小范数法是一种全局算法，其主要思想是寻求接近于真实相位分布的解包裹相位，使解包裹相位的局部微分尽可能与测量相位微分相一致。这个过程在数学上等价于下列 P 阶方程组

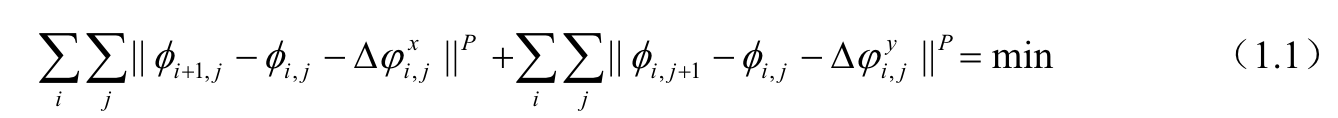
到目前为止，最小范数法中应用最多，最成功的主要是最小二乘算法(P=2)。Ghiglia和Romero[4]提出了二维相位解包裹的最小二乘算法。最小二乘解包裹算法是一种广泛使用的优化方法。这类算法基于包裹相位的离散偏微分与解包裹相位的离散偏微分之差最小的准则。基于最小二乘算法的二维相位解包裹分为加权和无加权两种形式。理论证明,无论是加权还是无加权的最小二乘相位解包裹都可以转化为一个求解离散泊松方程的过程

1、无加权的最小二乘相位解包裹算法 对于无加权最小二乘法所得到的泊松方程，任何可以有效地求解泊松方程的算法都可以用作相位解包裹,在无加权的情况下，基于快速傅立叶变换(FFT)[5]和离散余弦变换(DCT)[6]的方法得到广泛的应用。这两种方法通过计算离散域的变换可以快速得到所求的解，对一般表面的处理均可得到较好的结果，是较为实用的算法。

其中的一种经典算法是Gauss-Seidel松弛迭代法[7]，该算法首先将解空间初始化为0，然后通过迭代的形式进行计算，直到收敛为止。Gauss-Seidel迭代算法是一种典型的局域平滑算子,它可以迅速地去除信号中的高频成分,但对低频成分的滤除速度却非常慢,因此导致它很难收敛。为了提高运算效率,可采用多重网格技术[8]。多重网格方法的核心思想就是将低频成分转化为高频成分,加速Gauss-Seidel迭代算法的处理速度。这种由低频到高频的转换是通过网格重采样实现的。多重网格算法是一种经典的在较大网格上解决偏微分方程的快速算法, 在更粗、更小的网格上进行Gauss-Seidel迭代计算。一般地,对解决N×N网格上离散偏微分方程问题,多重网格算法与基于FFT的算法速度一样快。多重网格法可以解决更多的问题,包括非线性偏微分方程问题,并且多重网格算法对网格大小没有限制。

无权重的最小二乘算法具有算法简单、稳健的优点，尽管算法运算速度快,对内存要求小,但原始相位图中的坏数据或不一致区域会使最后的解包裹结果存

在误差，尤其是会对邻近区域的有效数据产生较大影响，产生与真实相位值偏差较大的解包裹相位，这可以通过引入相位数据的权重得以克服。 2、加权最小二乘去包裹算法 在无加权的最小二乘去包裹中，会在干涉图中的零幅值点、噪声点、低调制度点处及其周围点引起较大误差。为了消除或减少这些误差，可以采用加权最小二乘法。加权是最小二乘方法消除坡度低估效应、提高精度的必需选择。 加权最小二乘算法[6]是以非加权最小二乘法作为基础，其数学模型是较为复杂的泊松方程，只能通过采用迭代的方法无限逼近真解。求解加权最小二乘解的Picard迭代法[6]和共轭梯度法[9]通过加权矩阵可以实现对无效数据区域或不一致区域的屏蔽，消除坏数据对邻近区域数据的影响，算法的最大特点是稳健性好。Picard算法虽然收敛速度较慢，但其收敛准确度较高，实际中应用较多的是共轭梯度算法。 共轭梯度算法通过权系数的引进克服了无加权的最小二乘法的局限性，权系数使用经过二值化的质量图，它们的目的是对干涉相位图中由于残余点的存在而破坏的区域赋予零权，阻止它们对相位展开的破坏，共轭梯度算法首先使用无加权的最小二乘法作为预处理来加速收敛，之后采用共轭梯度算法迭代获得相位展开的结果。而预条件共轭梯度法[6]巧妙地将离散余弦变换和求解大型稀疏线性方程组的方法结合起来，可以实现有保证的、超线性的迭代收敛，因而收敛速度快。加权多重网格算法同样也是一种加权最小二乘去包裹算法，它引入多层次网格技术加快Gauss-Seidel迭代算法的执行速度,但与无加权算法有所不同。较预条件共轭梯度算法有更快的收敛速度，加权多网格算法在实际应用中的一个优点是运算速度快，算法较健壮，也是非常实用的算法。加权多重网格算法和共轭梯度方法在质量图较好的情况下能够得到较好的解[7]。 一般来说，如果权重引入适当，加权最小二乘法会对相位展开结果有所改善。但到目前为止，如何生成更适合相位解包裹的相位质量图仍没得到有效的解决，加权最小二乘法对解包裹相位质量的改善是有限的。而且加权最小二乘法不容易使用快速计算方法，计算速度慢，

最小二乘法是最小范数法中的一种，总体来说最小范数法解包裹的过程是一个曲面拟合的过程，选取不同的范数就确定了在保证解包裹相位梯度与包裹相位梯度之差最小的条件下，这种相位梯度之差的空间分布情况。当P≥2时，实际上人为的将相位曲面光滑化，必然造成解包裹相位误差，范数P越大则这种解包裹误差也越大。特别的，当P=0时，为最小0L范数法，这时解包裹相位梯度将与包裹相位梯度精确地保持一致，意味着寻求的是解包裹相位差与包裹相位差不相符的点数最少，这实际上与着眼于局部的路径跟踪算法的思想是一致的，算法的实质是对相位梯度进行拟合的过程。由于最小0L范数不会引入曲面拟合误差，因此在保持解包裹相位精确性方面是最优的，但是实现起来比较复杂，费时太多，对于一些特殊的干涉图可以作为一种选择。寻求全局最优的最小0L范数相位解包裹算法一直是该领域研究的方向之一