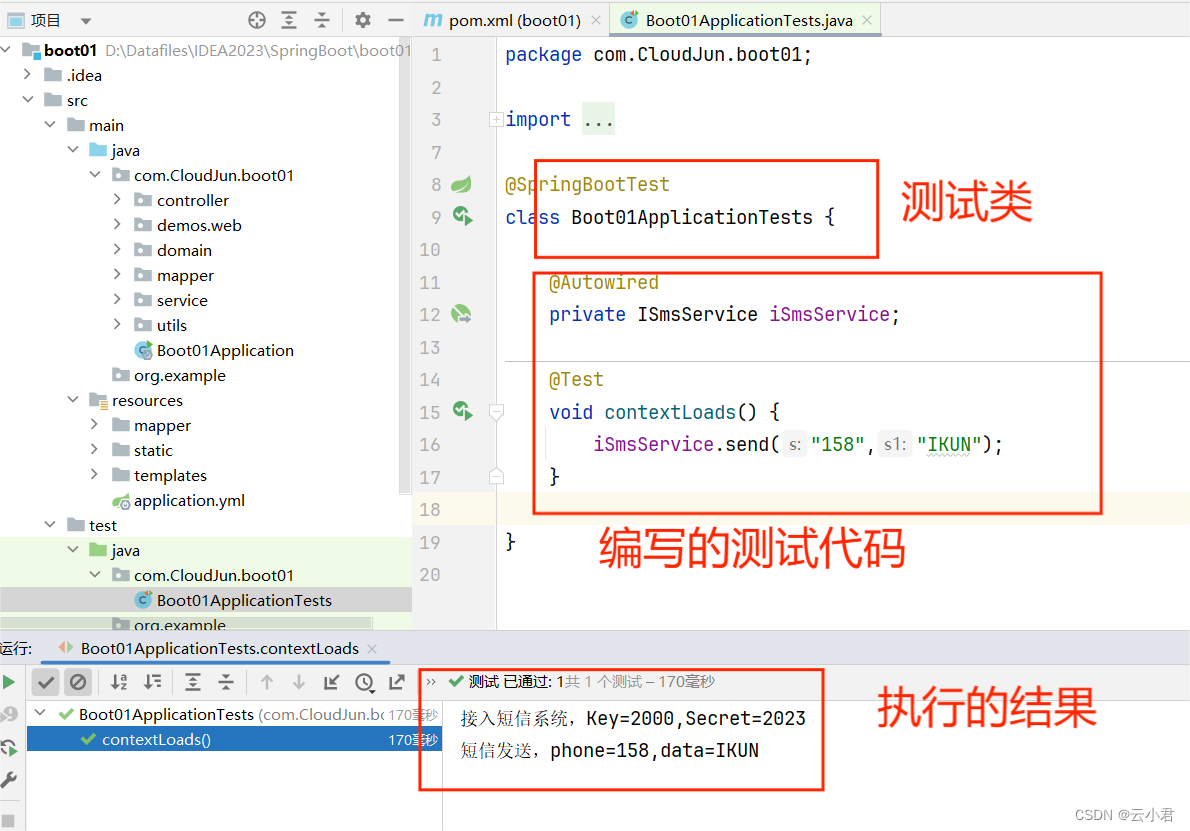
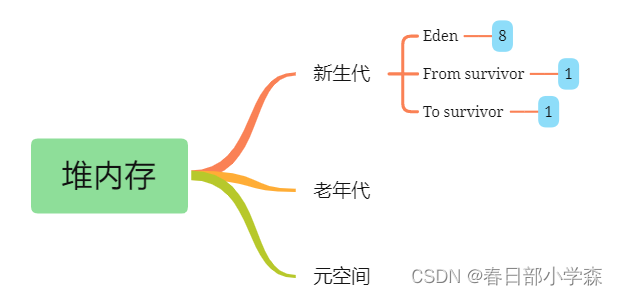
| 关卡名 | 回溯热门问题 | 我会了✔️ |
| 内容 | 1.组合总和问题 | ✔️ |
| 2.分割回文串问题 | ✔️ | |
| 3.子集问题 | ✔️ | |
| 4.排列问题 | ✔️ | |
| 5.字母全排列问题 | ✔️ | |
| 6.单词搜索 | ✔️ |
1. 组合总和问题
LeetCode39题目要求：给你一个无重复元素的整数数组candidates和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的 所有不同组合 ，并以列表形式返回。你可以按任意顺序返回这些组合。
candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同，则两种组合是不同的。 数组中的元素满足1 <= candidates[i] <= 200。例子：
输入：candidates = [2,3,6,7], target = 7
输出：[[2,2,3],[7]]
解释：
2 和 3 可以形成一组候选，2 + 2 + 3 = 7 。注意2可以使用多次。
7 也是一个候选， 7 = 7 ，仅有这两种组合。
如果不考虑重复，本题与LeetCode113题就是一个题，如果可以重复，那是否会无限制取下去呢？也不会，因为题目给了说明，每个元素最小为1，因此最多也就target个1。
我们画图看该怎么做，对于序列{2,3,6,7}，target=7。很显然我们可以先选择一个2，然后剩下的target就是7-2=5。再选一个2，剩余5-2=3。之后再选一个2，剩余3-2=1。已经小于2了，我们不能继续向下了，要返回一下。看看有没有3。OK，序列中有3，那么就得到了第一个结果{2,2,3}。
之后我们继续回退到只选了一个2的时候，这时候不能再取2了，而是从{3,6,7}中选择，如下图所示，没有符合要求的！
依次类推，后面尝试从3、6和7开始选择。
所以我们最终得到的结果就是{2,2,3}和{2,5}。为了方便，我们可以先对元素做个排序，然后将上面的过程画成这个一个树形图：
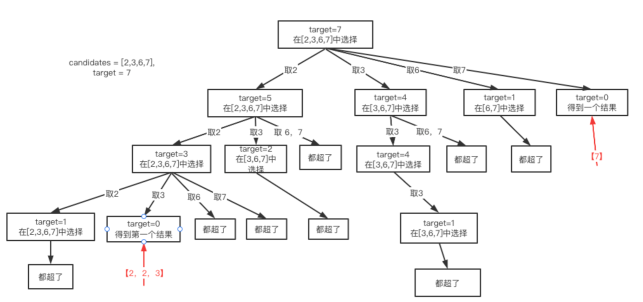
这个图横向是针对每个元素的暴力枚举，纵向是递归，也是一个纵横问题，实现代码也不复杂：
class CombinationSum {
List<List<Integer>> res = new ArrayList<>(); //记录答案
List<Integer> path = new ArrayList<>(); //记录当前正在访问的路径
public List<List<Integer>> combinationSum(int[] candidates, int target) {
dfs(candidates,0, target);
return res;
}
public void dfs(int[] c, int u, int target) {
if(target < 0){
return ;
}
if(target == 0)
{
res.add(new ArrayList(path));
return ;
}
for(int i = u; i < c.length; i++){
if( c[i] <= target)
{
path.add(c[i]);
//当前层将target减掉了一部分，也就是子结构只要找是否有满足(target - c[i])就可以了
dfs(c,i,target - c[i]); // 因为可以重复使用，所以还是i
path.remove(path.size()-1); //回溯
}
}
}
}2.分割回文串
分割问题也是回溯要解决的典型问题之一，常见的题目有分割回文串、分割IP地址，以及分割字符串等。
LeetCode131 分割回文串，给你一个字符串s，请你将s分割成一些子串，使每个子串都是回文串 ，返回s所有可能的分割方案。
回文串是正着读和反着读都一样的字符串。
示例1：
输入：s = "aab"
输出：[["a","a","b"],["aa","b"]]
字符串如何判断回文本身就是一个道算法题，本题在其之上还要再解决一个问题：如何切割？如果暴力切割，是非常困难的，如果从回溯的角度来思考就清晰很多：
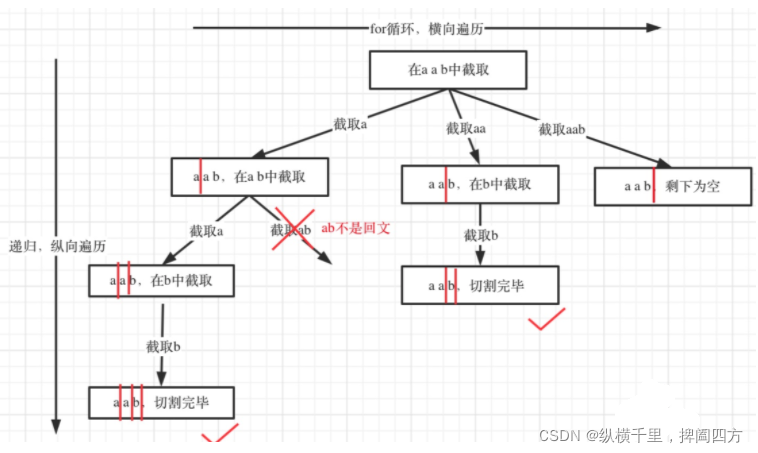我们说回溯本身仍然会进行枚举，这里的也一样。切割线（就是图中的红线）切割到字符串的结尾位置，说明找到了一个切割方法。这里就是先试一试,第一次切'a',第二次切'aa',第三次切'aab'。这对应的就是回溯里的for循环，也就是横向方面。
我们还说回溯仍然会进行递归，这里也是一样的，第一次切了'a',剩下的就是'ab'。递归就是再将其再切一个回文下来，也就是第二个'a',剩下的'b'再交给递归进一步切割。这就是纵向方面要干的事情，其他以此类推。
至于回溯操作与前面是一样的道理，不再赘述。通过代码就可以发现，切割问题的回溯搜索的过程和组合问题的回溯搜索的过程是差不多的。
class Partition {
List<List<String>> lists = new ArrayList<>();
Deque<String> deque = new LinkedList<>();
public List<List<String>> partition(String s) {
backTracking(s,0);
return lists;
}
private void backTracking(String s, int startIndex) {
//如果起始位置大于s的大小，说明找到了一组分割方案
if(startIndex>=s.length){
lists.add(new ArrayList(deque));
return;
}
for(int i=startIndex;i<s.length;i++){
//如果是回文子串，则记录
if(isPalindrome(s,startIndex,i)){
String str = s.substring(startIndex, i + 1);
deque.addLast(str);
} else {
continue;
}
//起始位置后移，保证不重复
backTracking(s,i+1);
deque.removeLast();
}
}
//判断是否是回文串
private boolean isPalindrome(String s, int startIndex, int end) {
for(int i=startIndex,j=end;i<j;i++,j--){
if(s.charAt(i)!=s.charAt(j)){
return false;
}
}
return true;
}
}3 子集问题
子集问题也是回溯的经典使用场景。回溯可以画成一种树状结构，子集、组合、分割问题都可以抽象为一棵树，但是子集问题与其他的类型有个明显的区别，组合问题一般找到满足要求的结果即可，而集合则要找出所有的情况。
LeetCode78，给你一个整数数组nums，数组中的元素互不相同。返回该数组所有可能的子集（幂集）。解集不能包含重复的子集。你可以按任意顺序返回解集。
示例1：
输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
看上面的例子nums = [1,2,3]，将子集抽象为树型结构如下：
从图中红线部分，可以看出遍历这个树的时候，把所有节点都记录下来，就是要求的子集集合。
这里什么时候要停下来呢？其实可以不加终止条件，因为startIndex >= nums.size()，本层for循环本来也结束了。
而且求取子集问题，不需要任何剪枝！因为子集就是要遍历整棵树。这样实现起来也比较容易。
class Subsets {
// 存放符合条件结果的集合
List<List<Integer>> result = new ArrayList<>();
// 用来存放符合条件结果
LinkedList<Integer> path = new LinkedList<>();
public List<List<Integer>> subsets(int[] nums) {
//空集合也是一个子集
if(nums.length==0){
result.add(new ArrayList<>());
return result;
}
subsetsHelper(nums,0);
return result;
}
private void subsetsHelper(int[] nums, int startIndex){
//「遍历这个树的时候，把所有节点都记录下来，就是要求的子集集合」。
result.add(new ArrayList<>(path));
if(startIndex>=nums.length){
return;
}
for(int i=startIndex;i<nums.length;i++){
path.add(nums[i]);
subsetsHelper(nums,i+1);
path.removeLast();
}
}
}上面代码里定义了全局变量result和path，这样整体比较简洁。这里可以转换成方法参数的形式，只是看起来比较复杂一些。
4 排列问题
LeetCode46.给定一个没有重复数字的序列，返回其所有可能的全排列。例如：
输入: [1,2,3]
输出: [ [1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1] ]
排列问题是典型的小学生都会，但是难道众人的问题。这个问题与前面组合等问题的一个区别是使用过的后面还要再用，例如1，在开始使用了，但是到了2 和3的时候仍然要再使用一次。这本质上是因为 [1,2] 和 [2,1] 从集合的角度看是一个，但从排列的角度看是两个。
元素1在[1,2]中已经使用过了，但是在[2,1]中还要再使用一次，所以就不能使用startIndex了，为此可以使用一个used数组来标记已经选择的元素，完整过程如图所示:
这里的终止条件怎么判断呢？从上图可以看出叶子节点就是结果。那什么时候是到达叶子节点呢？
当收集元素的数组path的大小达到和nums数组一样大的时候，说明找到了一个全排列，也表示到达了叶子节点。
class Permute {
List<List<Integer>> result = new ArrayList<>();
LinkedList<Integer> path = new LinkedList<>();
boolean[] used;
public List<List<Integer>> permute(int[] nums) {
if(nums.length==0){
return result;
}
used = new boolean(nums.length);
permuteHelper(nums);
return result;
}
private void permuteHelper(int[] nums){
if(path.size()==nums.length){
result.add(new ArrayList<>(path));
return;
}
for (int i = 0; i < nums.length; i++){
if (used[i]){
continue;
}
used[i] = true;
path.add(nums[i]);
permuteHelper(nums);
path.removeLast();
used[i] = false;
}
}
}5 字母大小写全排列
LeetCode784. 字母大小写全排列：给定一个字符串 s ，通过将字符串 s 中的每个字母转变大小写，我们可以获得一个新的字符串。返回所有可能得到的字符串集合。以任意顺序返回输出。
示例1：输入：s = "a1b2"
输出：["a1b2", "a1B2", "A1b2", "A1B2"]
如果本题去掉数字，只告诉你两个字母ab，让你每个字母变化大小写，那就是ab、Ab、aB、AB四种情况，题目比2.6电话号码问题还简单，这里的数字就是干扰项，我们需要做的是过滤掉数字， 只处理字母。另外还要添加个大小写转换的问题。如下图所示：
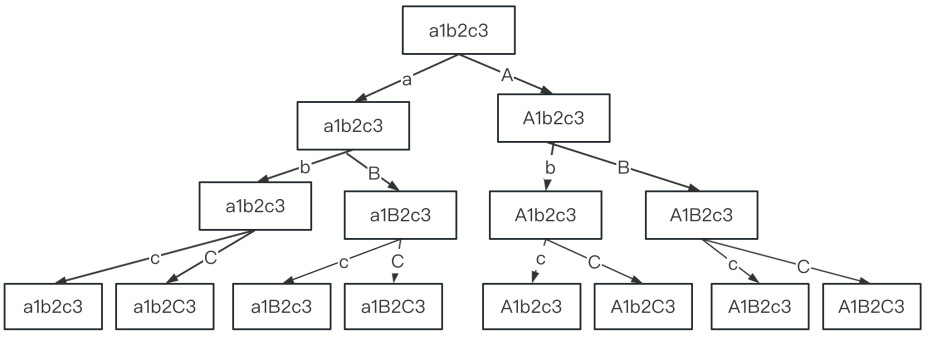
class LetterCasePermutation {
public List<String> letterCasePermutation(String s) {
List<String> ans = new ArrayList<String>();
dfs(s.toCharArray(), 0, ans);
return ans;
}
public void dfs(char[] arr, int pos, List<String> res) {
while (pos < arr.length && Character.isDigit(arr[pos])) {
pos++;
}
if (pos == arr.length) {
res.add(new String(arr));
return;
}
arr[pos] ^= 32;
dfs(arr, pos + 1, res);
arr[pos] ^= 32;
dfs(arr, pos + 1, res);
}
}6 单词搜索
LeetCode79.给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中，返回 true ；否则，返回 false 。
单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。
示例1：
输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
输出：true
思路：从上到下，左到右遍历网格，每个坐标递归调用dfs方法，方法里的i,j表示网格坐标，k表示word的第k个字符。
回溯最重要的是两个工作，一个是确定递归方法的终止条件，一个是确定递推公式，这两个是相辅相成的。
递归停止的场景我们来明确一下：
如果要返回 false ，则满足下面任何一种情况就可以，
- 行或列索引越界
- 当前矩阵元素与目标字符不同
- 当前矩阵元素已访问过。
如果要返回true，则应该k = len(word) - 1 ，即字符串 word 已全部匹配。
递推公式分析：
- 标记当前矩阵元素： 将 board[i][j] 修改为 空字符 '' ，代表此元素已访问过，防止之后搜索时重复访问。
- 搜索下一单元格： 朝当前元素的 上、下、左、右 四个方向开启下层递归，使用或连接 （代表只需找到一条可行路径就直接返回，不再做后续 DFS ），并记录结果至 res 。
- 还原当前矩阵元素： 将 board[i][j] 元素还原至初始值，即 word[k] 。
返回值： 返回布尔量 res ，代表是否搜索到目标字符串。
这样，看似高大上，实际并不复杂的实现就出来了：
class Exist {
public boolean exist(char[][] board, String word) {
char[] words = word.toCharArray();
for(int i = 0; i < board.length; i++) {
for(int j = 0; j < board[0].length; j++) {
if (dfs(board, words, i, j, 0)) return true;
}
}
return false;
}
boolean dfs(char[][] board, char[] word, int i, int j, int k) {
if (i >= board.length || i < 0 || j >= board[0].length || j < 0 || board[i][j] != word[k]) return false;
if (k == word.length - 1) return true;
board[i][j] = '\0';
boolean res = dfs(board, word, i + 1, j, k + 1) || dfs(board, word, i - 1, j, k + 1) ||
dfs(board, word, i, j + 1, k + 1) || dfs(board, word, i , j - 1, k + 1);
board[i][j] = word[k];
return res;
}
}
