Problem - C - Codeforces

题目大意：有一个n*m的网格，要求从(1,1)走到(n,m)，同时要求路径的长度必须为k+1，然后给每个两点之间的路径染成红色或蓝色，要求任意两个相邻线段颜色不能相同，求涂色的方案

3<=n,m<=16；1<=k<=1e9

思路：首先如果要从(1,1)走到(n,m)，最短路径上的线段数len=n-1+m+1，如果k<len，就没有构造方案，其他情况下，这个最短路上的颜色直接一个红一个蓝即可，接下来考虑我们还要走的k-len条线段，

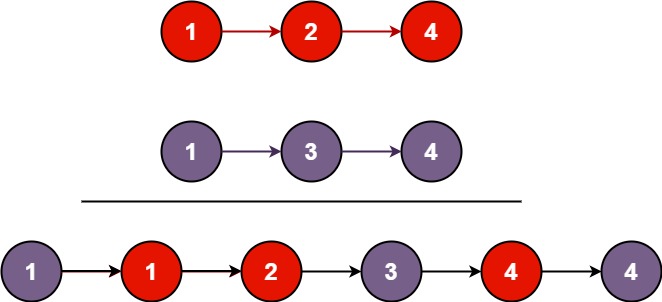
        在到达终点后，我们可以在终点所在的那个小正方形里绕圈，这样就能满足所有的k=len+4x，如下图中被圈起来的部分：

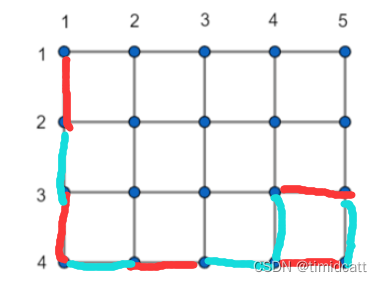
然后考虑其他的k能否被走出来，我们发现，如果在到终点前，在右下角的小三角上面绕一下，就可以走len+2步，然后因为n>=3，所以可以在右下再上面一个小正方形里绕圈，这样就得到了所有的k=len+2+4x，如下图：

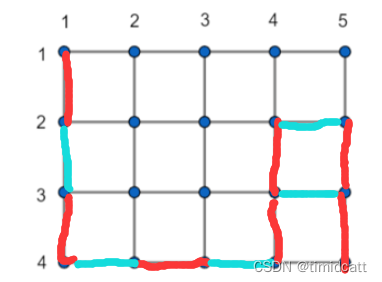
这样的话所有的偶数k-len就能都能找到一种合法的走法，然后发现如果k-len是奇数，无论如何都找不到一种走法，所以根据k和冷的关系分类讨论即可

#include<bits/stdc++.h>
//#include<__msvc_all_public_headers.hpp>
using namespace std;
typedef long long ll;
const int N = 2e5 + 5;
const ll MOD = 1e9 + 7;
int n;
int m;
ll a[N];
char ma1[20][20],ma2[20][20];
void init()
{
    for (int i = 1; i <= n; i++)
    {//先都初始化成任意颜色
        for (int j = 1; j <= m; j++)
        {
            ma1[i][j] = 'R';
            ma2[i][j] = 'R';
        }
    }
}
void solve()
{
    cin >> n;
    cin >> m;
    init();
    ll k;
    cin >> k;
    ll len = n - 1 + m - 1;
    if (k < len || (k - len) % 2 == 1)
    {//k<最短路或k-最短路是奇数，就没有合法路线
        cout << "NO\n";
        return;
    }
    cout << "YES\n";
    if ((k - len) % 4 == 0)
    {//k-len是4的倍数，就要去右下角的正方形绕圈
        for (int i = 1; i <= n-1; i++)
        {涂最左一列的最短路
            if (i & 1)
                ma1[i][1] = 'R';
            else
                ma1[i][1] = 'B';
        }
        if (ma1[n - 1][1] == 'R')
            ma2[n][1] = 'B';//涂最下面一行最短路
        else
        {
            ma2[n][1] = 'R';
        }
        for (int i = 2; i <= m-1; i++)
        {
            if (ma2[n][i-1] == 'R')
                ma2[n][i] = 'B';
            else
                ma2[n][i] = 'R';
        }
        if (ma2[n][m - 1] == 'R')//涂右下角的小正方形
            ma1[n - 1][m] = ma1[n - 1][m - 1] = 'B';
        else
            ma1[n - 1][m] = ma1[n - 1][m - 1] = 'R';
        ma2[n - 1][m - 1] = ma2[n][m - 1];
        for (int i = 1; i <= n; i++)
        {
            for (int j = 1; j <= m - 1; j++)
            {
                cout << ma2[i][j] << " ";
            }
            cout << '\n';
        }
        for (int i = 1; i <= n - 1; i++)
        {
            for (int j = 1; j <= m; j++)
            {
                cout << ma1[i][j] << " ";
            }
            cout << '\n';
        }
        return;
    }
    if ((k - len - 2) % 4 == 0)
    {//k-len-2是4的倍数，最后一个小正方形往上绕
        for (int i = 1; i <= n - 1; i++)
        {//涂最左一列
            if (i & 1)
                ma1[i][1] = 'R';
            else
                ma1[i][1] = 'B';
        }
        if (ma1[n - 1][1] == 'R')
            ma2[n][1] = 'B';//涂最下面一行
        else
        {
            ma2[n][1] = 'R';
        }
        for (int i = 2; i <= m - 1; i++)
        {
            if (ma2[n][i - 1] == 'R')
                ma2[n][i] = 'B';
            else
                ma2[n][i] = 'R';
        }
        if (ma2[n][m - 2] == 'R')//涂右下角小正方形
            ma1[n - 1][m] = ma1[n - 1][m - 1] = 'B';
        else
            ma1[n - 1][m] = ma1[n - 1][m - 1] = 'R';
        ma2[n - 1][m - 1] = ma2[n][m - 2];//涂右下角上面一个小正方形
        if (ma2[n - 1][m - 1] == 'R')
        {
            ma1[n - 2][m] = ma1[n - 2][m - 1] = 'B';
        }
        else
        {
            ma1[n - 2][m] = ma1[n - 2][m - 1] = 'R';
        }
        ma2[n - 2][m - 1] = ma2[n - 1][m - 1];
        for (int i = 1; i <= n; i++)
        {
            for (int j = 1; j <= m - 1; j++)
            {
                cout << ma2[i][j] << " ";
            }
            cout << '\n';
        }
        for (int i = 1; i <= n - 1; i++)
        {
            for (int j = 1; j <= m; j++)
            {
                cout << ma1[i][j] << " ";
            }
            cout << '\n';
        }
    }
    cout << '\n';
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    int t;
    cin >> t;
    while (t--)
    {
        solve();
    }
    return 0;
}