本篇总结的是最小生成树算法

生成树

连通图中的每一棵生成树，都是原图的一个极大无环子图，即：从其中删去任何一条边，生成树就不在连通；反之，在其中引入任何一条新边，都会形成一条回路。若连通图由n个顶点组成，则其生成树必含n个顶点和n-1条边。因此构造最小生成树的准则有三条：

1. 只能使用图中的边来构造最小生成树
2. 只能使用恰好n-1条边来连接图中的n个顶点
3. 选用的n-1条边不能构成回路
   构造最小生成树的方法：Kruskal算法和Prim算法。这两个算法都采用了逐步求解的贪心策略
   贪心算法：是指在问题求解时，总是做出当前看起来最好的选择。也就是说贪心算法做出的不是整体
   最优的的选择，而是某种意义上的局部最优解。贪心算法不是对所有的问题都能得到整体最优解

Kruskal算法

任给一个有n个顶点的连通网络N={V,E}

首先构造一个由这n个顶点组成、不含任何边的图G={V,NULL}，其中每个顶点自成一个连通分量，其次不断从E中取出权值最小的一条边(若有多条任取其一)，若该边的两个顶点来自不同的连通分量，则将此边加入到G中。如此重复，直到所有顶点在同一个连通分量上为止

核心：每次迭代时，选出一条具有最小权值，且两端点不在同一连通分量上的边，加入生成树

以下面这个图为例，模拟一次最小生成树的过程

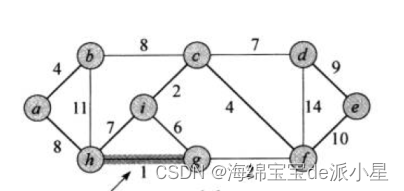
下面进行这个生成树的代码实现逻辑

整体来说就是最小生成树的逻辑，那么基于这个逻辑就可以完成代码的编写了

// 利用Kruskal算法求最小生成树
W Kruskal(Self& mintree)
{
	mintree._matrix.resize(_matrix.size());
	for (auto& e : mintree._matrix)
		e.resize(_matrix[0].size());
	mintree._vertexs = _vertexs;
	mintree._vIndexMap = _vIndexMap;
	// 顶点之间的连通性可以用并查集来表示，选点可以用优先级队列来选
	UnionFindSet ufs(_vertexs.size());
	priority_queue < Edge, vector<Edge>, greater<Edge>> minheap;
	// 把顶点的信息存储到优先级队列中
	for (size_t i = 0; i < _matrix.size(); i++)
		for (size_t j = 0; j < _matrix[i].size(); j++)
			minheap.push(Edge(i, j, _matrix[i][j]));
	W maxW = W();
	while (!minheap.empty())
	{
		Edge cur = minheap.top();
		minheap.pop();
		// 如果当前边对应的两个顶点不连同，那么就可以作为最小边
		if (!ufs.IsSame(cur._dsti, cur._srci))
		{
			ufs.merge(cur._dsti, cur._srci);
			mintree._AddEdge(cur._srci, cur._dsti, cur._w);
			maxW += cur._w;
		}
	}
	return maxW;
}

Prim算法

以上面的步骤为例，完整的进行一次Prim算法的实现过程

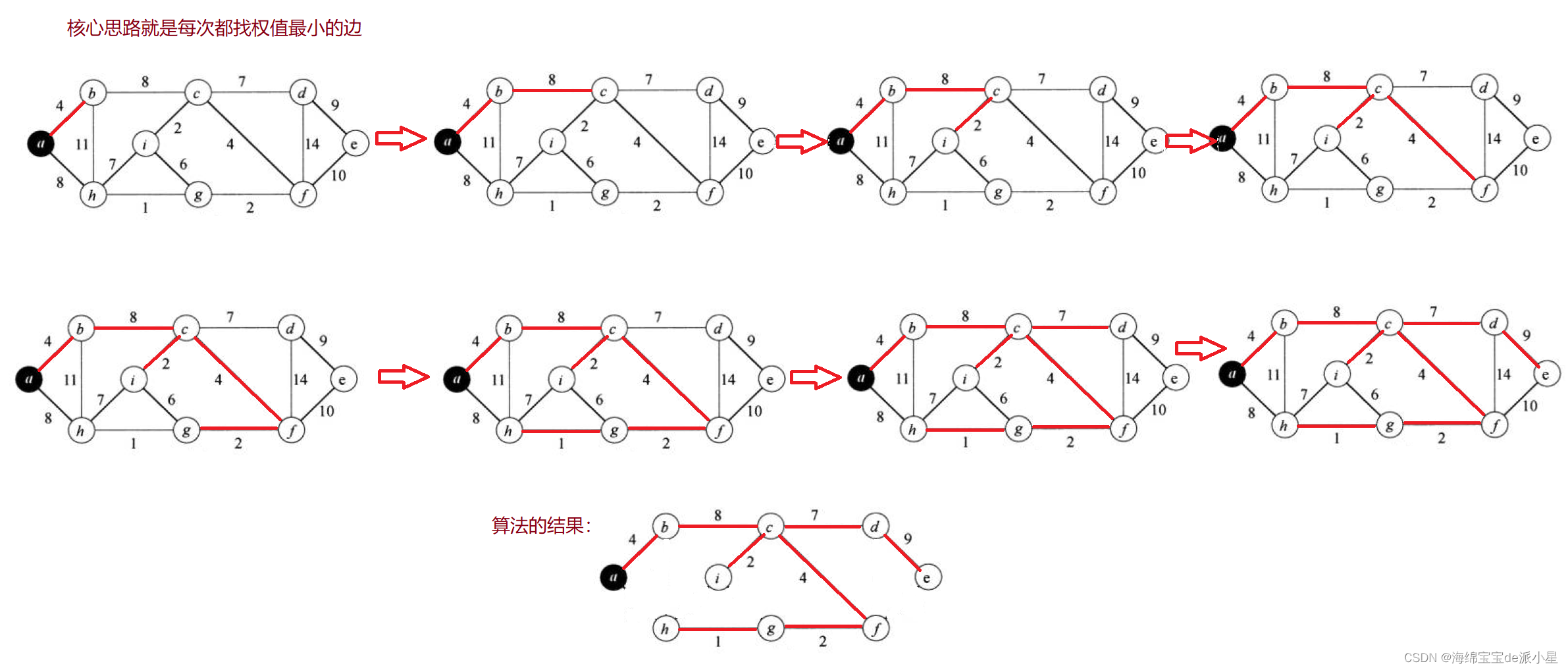
下面用代码来实现一下Prim算法

		// 利用Prim算法求最小生成树
		W Prim(const V& Vertex, Self& mintree)
		{
			// 进行初始化
			mintree._matrix.resize(_matrix.size());
			for (auto& e : mintree._matrix)
				e.resize(_matrix[0].size(), W_MAX);
			mintree._vertexs = _vertexs;
			mintree._vIndexMap = _vIndexMap;
			// 用一个set集合存储的是已经使用过的顶点信息
			set<size_t> inset;
			priority_queue<Edge, vector<Edge>, greater<Edge>> minheap;
			size_t srci = GetVertexsIndex(Vertex);
			inset.insert(srci);
			// 把和这个顶点相连的边的信息都存储起来
			for (size_t i = 0; i < _matrix[srci].size(); i++)
				if (_matrix[srci][i] != W_MAX)
					minheap.push(Edge(srci, i, _matrix[srci][i]));
			W totalw = W();
			while (inset.size() < _vertexs.size() && !minheap.empty())
			{
				// 把最小权值的边取出来
				Edge minEdge = minheap.top();
				minheap.pop();
				// 如果这个边的两个顶点有一个不在集合中，那么就可以构成一个不会变成环的树
				if (inset.find(minEdge._dsti) == inset.end() || inset.find(minEdge._srci) == inset.end())
				{
					// 那么这个边就可以被使用
					//cout << _vertexs[minEdge._srci] << "->" << _vertexs[minEdge._dsti]<<" " << minEdge._w << endl;
					mintree._AddEdge(minEdge._srci, minEdge._dsti, minEdge._w);
					totalw += minEdge._w;
					// 再把和这个边相邻的边都加到队列中，供下一次寻找使用
					for(size_t i = 0; i < _matrix[minEdge._dsti].size(); i++)
						if (_matrix[minEdge._dsti][i] != W_MAX && inset.find(i) == inset.end())
							minheap.push(Edge(minEdge._dsti, i, _matrix[minEdge._dsti][i]));
					inset.insert(minEdge._dsti);
				}
			}
			if (inset.size() == _vertexs.size()) 
				return totalw;
			else
				return W();
		}