1.了解数据结构和算法
1.1 二分查找
二分查找(Binary Search)是一种在有序数组中查找特定元素的搜索算法。它的基本思想是将数组分成两半,然后比较目标值与中间元素的大小关系,从而确定应该在左半部分还是右半部分继续查找。这个过程不断重复,直到找到目标值或确定它不存在于数组中。
1.1.1 二分查找的实现
(1)循环条件使用 "i <= j" 而不是 "i < j" 是因为,在二分查找的过程中,我们需要同时更新 i 和 j 的值。当 i 和 j 相等时,说明当前搜索范围只剩下一个元素,我们需要检查这个元素是否是我们要找的目标值。如果这个元素不是我们要找的目标值,那么我们可以确定目标值不存在于数组中。
如果我们将循环条件设置为 "i < j",那么当 i 和 j 相等时,我们就无法进入循环来检查这个唯一的元素,这会导致我们无法准确地判断目标值是否存在。
因此,在二分查找的循环条件中,我们应该使用 "i <= j",以确保我们在搜索范围内包含所有可能的元素。
(2)如果你使用 "i + j / 2" 来计算二分查找的中间值,可能会遇到整数溢出的问题。这是因为在 Java 中,整数除法(/)对整数操作时会向下取整,结果仍然是一个整数。例如,如果
i和j都是很大的数,且它们相加结果大于Integer.MAX_VALUE(即 2^31 - 1),那么直接将它们相加再除以 2 就会导致溢出,因为中间结果已经超出了int类型的最大值(会变成负数)。public static void main(String[] args) { int[]arr={1,22,33,55,88,99,117,366,445,999}; System.out.println(binarySearch( arr,1));//结果:0 System.out.println(binarySearch( arr,22));//结果:1 System.out.println(binarySearch( arr,33));//结果:2 System.out.println(binarySearch( arr,55));//结果:3 System.out.println(binarySearch( arr,88));//结果:4 System.out.println(binarySearch( arr,99));//结果:5 System.out.println(binarySearch( arr,117));//结果:6 System.out.println(binarySearch( arr,366));//结果:7 System.out.println(binarySearch( arr,445));//结果:8 System.out.println(binarySearch( arr,999));//结果:9 System.out.println(binarySearch( arr,1111));//结果:-1 System.out.println(binarySearch( arr,-1));//结果:-1 } /** * @Description * @Author LY * @Param [arr, target] 待查找升序数组,查找的值 * @return int 找到返回索引,找不到返回-1 * @Date 2023/12/8 16:38 **/ public static int binarySearch(int[] arr, int target){ //设置 i跟j 初始值 int i=0; int j= arr.length-1; //如果i>j,则表示并未找到该值 while (i<=j){ int m=(i+j)>>>1; // int m=(i+j)/2; if (target<arr[m]){ //目标在左侧 j=m-1; }else if(target>arr[m]){ //目标在右侧 i=m+1; }else{ //相等 return m; } } return -1; }
1.1.2 二分查找改动版
方法
binarySearchAdvanced是一个优化版本的二分查找算法。它将数组范围从 0 到arr.length进行划分(改动1),并且在循环条件中使用i < j而不是i <= j(改动2)。这种修改使得当目标值不存在于数组中时,可以更快地结束搜索。此外,在向左移动右边界时,只需将其设置为中间索引m而不是m - 1(改动3)。这些改动使
binarySearchAdvanced在某些情况下可能比标准二分查找更快。然而,在实际应用中,这些差异通常很小,因为二分查找本身的复杂度已经很低(O(log n))。/** * @return int 找到返回索引,找不到返回-1 * @Description 二分查找改动版 * @Author LY * @Param [arr, target] 待查找升序数组,查找的值 * @Date 2023/12/8 16:38 **/ public static int binarySearchAdvanced(int[] arr, int target) { int i = 0; // int j= arr.length-1; int j = arr.length;//改动1 // while (i<=j){ while (i < j) {//改动2 int m = (i + j) >>> 1; if (target < arr[m]) { // j = m - 1; j = m; //改动3 } else if (arr[m] < target) { i = m + 1; } else { return m; } } return -1; }
1.2 线性查找
线性查找(Linear Search)是一种简单的搜索算法,用于在无序数组或列表中查找特定元素。它的基本思想是从数组的第一个元素开始,逐一比较每个元素与目标值的大小关系,直到找到目标值或遍历完整个数组。
(1)初始化一个变量 index 为 -1,表示尚未找到目标值。
(2)从数组的第一个元素开始,使用循环依次访问每个元素:
(3)如果当前元素等于目标值,则将 index 设置为当前索引,并结束循环。(4)返回 index。(如果找到了目标值返回其索引;否则返回 -1 表示未找到目标值)
/** * @return int 找到返回索引,找不到返回-1 * @Description 线性查找 * @Author LY * @Param [arr, target] 待查找数组(可以不是升序),查找的值 * @Date 2023/12/8 16:38 **/ public static int LinearSearch(int[] arr, int target) { int index=-1; for (int i = 0; i < arr.length; i++) { if(arr[i]==target){ index=i; break; } } return index; }
1.3 衡量算法第一因素
时间复杂度:算法在最坏情况下所需的基本操作次数与问题规模之间的关系。
1.3.1 对比
假设每行代码执行时间都为t,数据为n个,且是最差的执行情况(执行最多次):
二分查找:
二分查找执行时间为: 5L+4:
既5*floor(log_2(x)+1)+4执行语句 执行次数 int i=0; 1 int j=arr.length-1; 1 return -1; 1 循环次数为:floor(log_2(n))+1,之后使用L代替 i<=j; L+1 int m= (i+j)>>>1; L artget<arr[m] L arr[m]<artget L i=m+1; L 线性查找:
线性查找执行时间为: 3x+3 执行语句 执行次数 int i=0; 1 i<a.length; x+1 i++; x arr[i]==target x return -1; 1 对比工具:Desmos | 图形计算器
对比结果:
随着数据规模增加,线性查找执行时间会逐渐超过二分查找。
1.3.2 时间复杂度
计算机科学中,时间复杂度是用来衡量一个算法的执行,随着数据规模增大,而增长的时间成本(不依赖与环境因素)。
时间复杂度的标识:
假设要出炉的数据规模是n,代码总执行行数用f(n)来表示:
线性查找算法的函数:f(n)=3*n+3。
二分查找算法函数::f(n)=5*floor(log_2(x)+1)+4。
为了简化f(n),应当抓住主要矛盾,找到一个变化趋势与之相近的表示法。
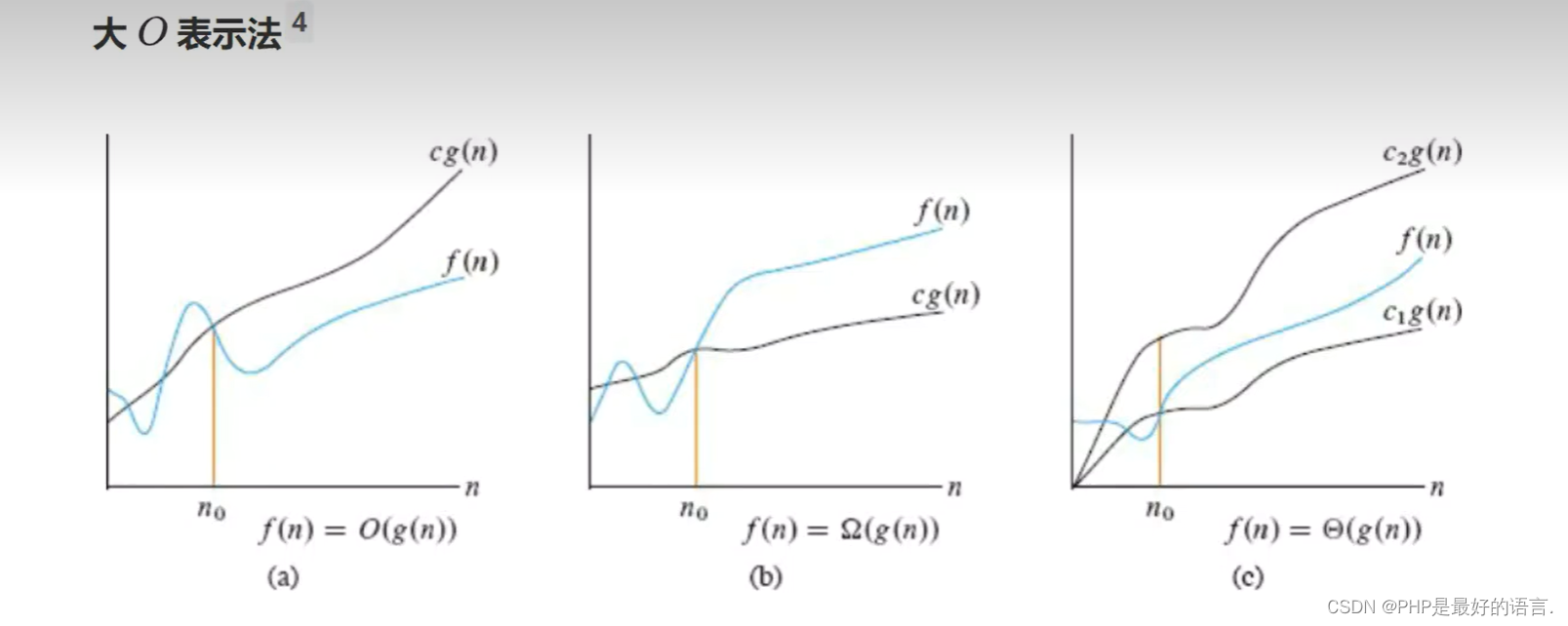
1.3.3 渐进上界
渐进上界代表算法执行的最差情况:
以线性查找法为例:
f(n)=3*n+3
g(n)=n
取c=4,在n0=3后,g(n)可以作为f(n)的渐进上界,因此大O表示法写作O(n)
以二分查找为例:
5*floor(log_2(n)+1)+4===》5*floor(log_2(n))+9
g(n)=log_2(n)
O(log_2(n))
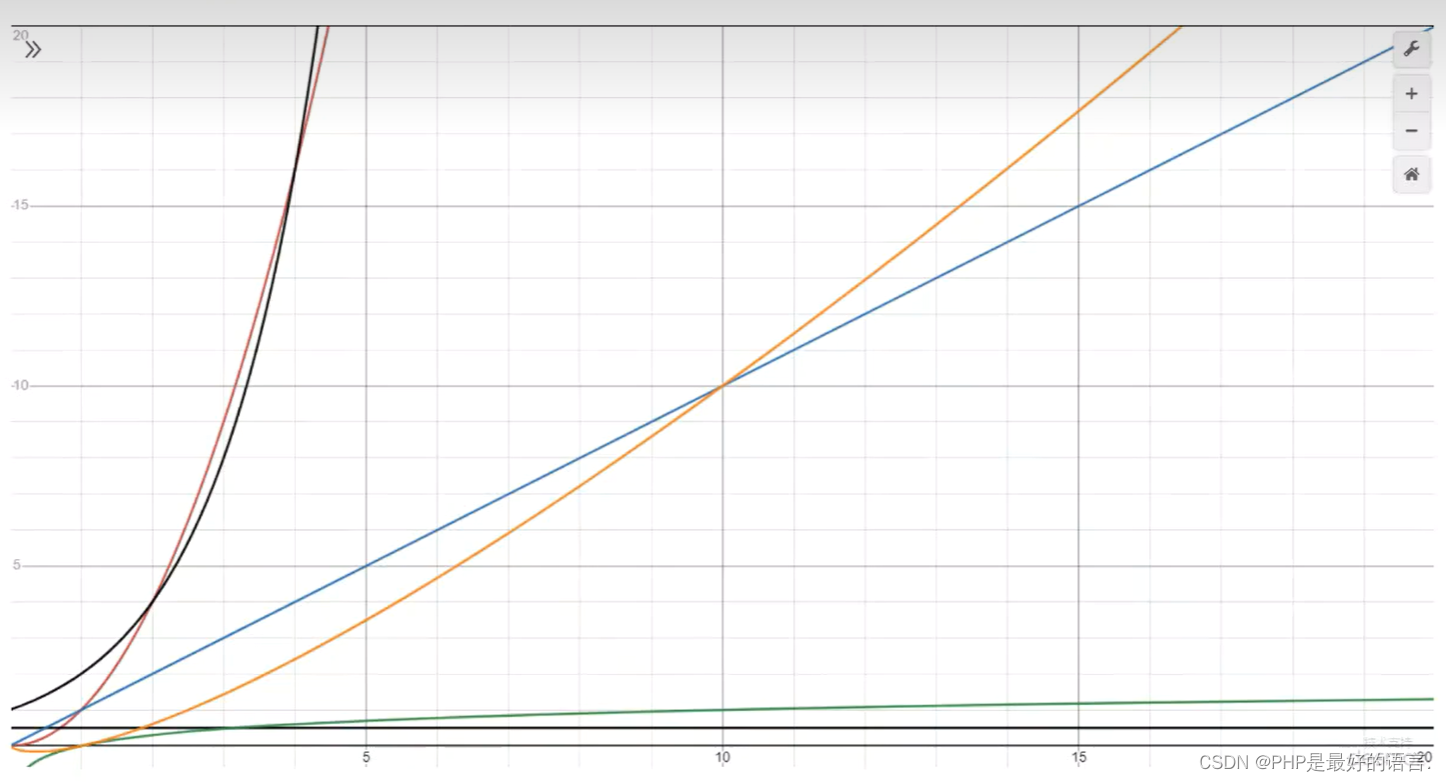
1.3.4 常见大O表示法
按时间复杂度,从低到高:
(1)黑色横线O(1):常量时间复杂度,意味着算法时间并不随数据规模而变化。
(2)绿色O(log(n)):对数时间复杂度。
(3)蓝色O(n):线性时间复杂度,算法时间与规模与数据规模成正比。
(4)橙色O(n*log(n)):拟线性时间复杂度。
(5)红色O(n^2):平方时间复杂度。
(6)黑色向上O(2^n):指数时间复杂度。
(7)O(n!):这种时间复杂度非常大,通常意味着随着输入规模 n 的增加,算法所需的时间会呈指数级增长。因此,具有 O(n!) 时间复杂度的算法在实际应用中往往是不可行的,因为它们需要耗费大量的计算资源和时间。
1.4 衡量算法第二因素
空间复杂度:与时间复杂度类似,一般也用O衡量,一个算法随着数据规模增大,而增长的额外空间成本。
1.3.1 对比
以二分查找为例:
二分查找占用空间为: 4字节 执行语句 执行次数 int i=0; 4字节 int j=arr.length-1; 4字节 int m= (i+j)>>>1; 4字节 二分查找占用空间复杂度为: O(1) 性能分析:
时间复杂度:
最坏情况:O(log(n))。
最好情况:待查找元素在数组中央,O(1)。
空间复杂度:需要常熟个数指针:i,j,m,额外占用空间是O(1)。
1.5 二分查找改进
在之前的二分查找算法中,如果数据在数组的最左侧,只需要执行L次 if 就可以了,但是如果数组在最右侧,那么需要执行L次 if 以及L次 else if,所以二分查找向左寻找元素,比向右寻找元素效率要高。
(1)左闭右开的区间,i指向的可能是目标,而j指向的不是目标。
(2)不在循环内找出,等范围内只剩下i时,退出循环,再循环外比较arr[i]与target。
(3)优点:循环内的平均比较次数减少了。
(4)缺点:时间复杂度:θ(log(n))。
1.6 二分查找相同元素
1.6.1 返回最左侧
当有两个数据相同时,上方的二分查找只会返回中间的元素,而我们想得到最左侧元素就需要对算法进行改进。(Leftmost)
public static void main(String[] args) { int[] arr = {1, 22, 33, 55, 99, 99, 99, 366, 445, 999}; System.out.println(binarySearchLeftMost1(arr, 99));//结果:4 System.out.println(binarySearchLeftMost1(arr, 999));//结果:9 System.out.println(binarySearchLeftMost1(arr, 998));//结果:-1 } /** * @return int 找到相同元素返回返回最左侧查找元素索引,找不到返回-1 * @Description 二分查找LeftMost * @Author LY * @Param [arr, target] 待查找升序数组,查找的值 * @Date 2023/12/8 16:38 **/ public static int binarySearchLeftMost1(int[] arr, int target) { int i = 0; int j = arr.length - 1; int candidate = -1; while (i <= j) { int m = (i + j) >>> 1; if (target < arr[m]) { j = m - 1; } else if (arr[m] < target) { i = m + 1; } else { // return m; 查找到之后记录下来 candidate=m; j=m-1; } } return candidate; }
1.6.2 返回最右侧
当有两个数据相同时,上方的二分查找只会返回中间的元素,而我们想得到最右侧元素就需要对算法进行改进。(Rightmost)
public static void main(String[] args) { int[] arr = {1, 22, 33, 55, 99, 99, 99, 366, 445, 999}; System.out.println(binarySearchRightMost1(arr, 99));//结果:6 System.out.println(binarySearchRightMost1(arr, 999));//结果:9 System.out.println(binarySearchRightMost1(arr, 998));//结果:-1 } /** * @return int 找到相同元素返回返回最右侧侧查找元素索引,找不到返回-1 * @Description 二分查找RightMost * @Author LY * @Param [arr, target] 待查找升序数组,查找的值 * @Date 2023/12/8 16:38 **/ public static int binarySearchRightMost1(int[] arr, int target) { int i = 0; int j = arr.length - 1; int candidate = -1; while (i <= j) { int m = (i + j) >>> 1; if (target < arr[m]) { j = m - 1; } else if (arr[m] < target) { i = m + 1; } else { // return m; 查找到之后记录下来 candidate=m; i = m + 1; } } return candidate; }
1.6.3 优化
将leftMost优化后,可以在未找到目标值的情况下,返回大于等于目标值最靠左的一个索引。
/** * @return int 找到相同元素返回返回最左侧查找元素索引,找不到返回i * @Description 二分查找LeftMost * @Author LY * @Param [arr, target] 待查找升序数组,查找的值 * @Date 2023/12/8 16:38 **/ public static int binarySearchLeftMost2(int[] arr, int target) { int i = 0; int j = arr.length - 1; while (i <= j) { int m = (i + j) >>> 1; if (target <= arr[m]) { j = m - 1; } else { i = m + 1; } } return i; }将rightMost优化后,可以在未找到目标值的情况下,返回小于等于目标值最靠右的一个索引。
1.6.4 应用场景
1.6.4.1 查排名
(1)查找排名:
在执行二分查找时,除了返回目标值是否存在于数组中,还可以记录查找过程中遇到的目标值的位置。如果找到了目标值,则直接返回该位置作为排名;如果没有找到目标值,但知道它应该插入到哪个位置才能保持数组有序,则可以返回这个位置作为排名。leftMost(target)+1
(2)查找前任(前驱):
如果目标值在数组中存在,并且不是数组的第一个元素,那么其前任就是目标值左边的一个元素。我们可以在找到目标值之后,再调用一次二分查找函数,这次查找的目标值设置为比当前目标值小一点的数。这样就可以找到目标值左侧最接近它的元素,即前任。leftMost(target)-1
(3)查找后任(后继):
如果目标值在数组中存在,并且不是数组的最后一个元素,那么其后任就是目标值右边的一个元素。类似地,我们可以在找到目标值之后,再调用一次二分查找函数,这次查找的目标值设置为比当前目标值大一点的数。这样就可以找到目标值右侧最接近它的元素,即后任。rightMost(target)+1
(3)最近邻居:
前任和后任中,最接近目标值的一个元素。
1.6.4.2 条件查找元素
(1)小于某个值:0 ~ leftMost(target)-1
(2)小于等于某个值:0 ~ rightMost(target)
(3)大于某个值:rightMost(target)+1 ~ 无穷大
(4)大于等于某个值:leftMost(4) ~ 无穷大
(5)他们可以组合使用。
2. 基础数据结构-数组
2.1 概念
数组是一种数据结构,它是一个由相同类型元素组成的有序集合。在编程中,数组的定义是创建一个具有特定大小和类型的存储区域来存放多个值。数组可以是一维、二维或多维的。每个元素至少有一个索引或键来标识。
2.2 数组特点
(1)固定大小:数组的大小在创建时就被确定下来,并且不能在后续操作中更改。这意味着一旦创建了数组,就不能添加或删除元素(除非使用新的数组来替换旧的数组)。
(2)相同数据类型:数组中的所有元素必须是同一数据类型的。例如,一个整数数组只能存储整数,而不能混杂着字符串或其他类型的数据。
(3)连续内存空间:数组中的元素在内存中是连续存放的。
(4)索引访问:数组元素是通过索引来访问的,索引通常从0开始。因此,第一个元素的索引是0,第二个元素的索引是1,以此类推。
(5)高效的随机访问:由于数组元素在内存中是连续存放的,所以可以快速地通过索引访问到任何一个元素,时间复杂度为O(1)。
(6)有序性:虽然数组本身并没有规定其元素必须按照特定顺序排列,但通常在编程中会把数组看作是有序的数据结构,因为它的元素是按索引顺序存储的。
(7)可变性:数组中元素值是可改变的,只要该元素的数据类型与数组元素类型兼容即可。
(8)一维、二维或多维:数组可以是一维的(即线性的),也可以是二维或多维的。多维数组通常用于表示表格数据或其他复杂的网格结构。这些特性使得数组在许多场景下非常有用,尤其是在需要对大量同类型数据进行高效访问和处理的时候。
2.3 数组特点(扩展)
2.3.1 数组的存储
因为数组中的元素在内存中是连续存放的。这意味着可以通过计算每个元素相对于数组开始位置的偏移量来访问它们,从而提高访问速度。 数组起始地址为BaseAddress,可以使用公式BaseAddress+ i *size,计算出索引 i 元素的地址,i 即是索引,java和C等语言中,都是从0开始。size是每个元素占用的字节,例如int占用4字节,double占用8字节。
因此,数组的随机访问和数据规模无关,时间复杂度为O(1)。
2.3.2 空间占用
JAVA的数组结构包含:markword(8字节),class指针(4字节),数组大小(4字节)。
(1)数组本身是一个对象。每个Java对象都有一个对象头(Object Header),其中包含了类指针和Mark Word等信息。。Mark Word是HotSpot虚拟机设计的一种数据结构,用于存储对象的运行时元数据。
(2)Mark Word的作用主要包括:
(2.1)对象的锁状态:Mark Word中的部分内容会根据对象是否被锁定而改变。例如,如果数组正在被synchronized同步块或方法保护,那么这部分内容将包含有关锁的信息,如线程ID、锁状态等。
(2.2)垃圾收集信息:Mark Word还存储了与垃圾收集相关的信息,如对象的分代年龄和类型指针等。这对于垃圾收集器跟踪和回收对象非常关键。
其他标志位:除此之外,Mark Word可能还包括一些其他的标志位,如偏向锁标志、轻量级锁标志等。
(2.3)需要注意的是,由于Mark Word是为整个对象服务的,所以它并不直接针对数组元素。数组元素的数据是存储在对象头之后的实例数据区域中。Mark Word主要是为了支持JVM进行各种操作,比如内存管理和并发控制等。(3)类指针:类指针指向的是该对象所属的类元数据(Class Metadata)。这个指针对于运行时的动态绑定、方法调用以及反射操作非常重要。它存储了关于对象类型的所有信息,包括类名、父类、接口、字段、方法、常量池等。在64位JVM上,类指针通常占用8字节。而在32位JVM上,类指针占用4字节。
(4)数组大小:数组大小为4字节,因此决定了数组最大容量为2^32,数组元素+字节对齐(JAVA中所有对象的大小都是8字节的整数倍,不足的要用对齐字节补足)
例如:
int [] arr={1,2,3,4,5}该数组包含内容包括:
单位(字节)
markword(8) class指针(4) 数组大小(4) 1(4) 2(4) 3(4) 4(4) 5(4) 字节对齐(4) 大小为:8+4+4+4*4+4+4=40字节
2.3.3 动态数组
因为数组的大小是固定的,所以数组中的元素并不能随意地添加和删除。这种数组称之为静态数组。
JAVA中的ArrayList是已经创建好的动态数组。
插入或者删除性能时间复杂度:
头部位置:O(n)
中间位置:O(n)
尾部位置:O(1) 均摊来说
package org.alogorithm; import java.util.Arrays; import java.util.Iterator; import java.util.function.Consumer; import java.util.stream.IntStream; public class Main02 { public static void main(String[] args) { MyArray myArray = new MyArray(); myArray.addLast(1); myArray.addLast(2); myArray.addLast(3); myArray.addLast(4); myArray.addLast(5); myArray.addLast(7); myArray.addLast(8); myArray.addLast(9); myArray.addLast(10); myArray.addLast(11); /*for (int i = 0; i < myArray.size; i++) { System.out.println(myArray.array[i]); }*/ myArray.foreach((e) -> { //具体操作由调用方界定 System.out.println(e + "Consumer"); }); myArray.add(2, 6); for (Integer integer : myArray) { System.out.println(integer + "Iterable"); } System.out.println(myArray.remove(4)+"元素被删除"); myArray.stream().forEach(e -> { System.out.println(e + "stream"); }); } static class MyArray implements Iterable<Integer> { private int size = 0;//逻辑大小 private int capacity = 8;//容量 private int[] array = {}; public void addLast(int value) { /*array[size] = value; size++;*/ add(size, value); } public void add(int index, int value) { //容量不够扩容 checkAndGrow(); /* * param1 :要copy的数组 * param1 :copy的起始位置 * param1 :要存放数组 * param1 :要copy的个数 * 这个方法表示要将array从index开始copy到index+1的位置, * copy的个数是数组的大小-index(index向后的元素) * */ if (index >= 0 && index <= size) { System.arraycopy(array, index, array, index + 1, size - index); } //合并add方法 array[index] = value; size++; } private void checkAndGrow() { if (size==0){ array=new int[capacity]; }else if (size == capacity) { capacity+=capacity>>1; int[] newArray = new int[capacity]; //赋值数组 System.arraycopy(array,0,newArray,0,size); array=newArray; } } //查询元素 public int get(int index) { return array[index]; } //遍历数组 1 //查询元素 public void foreach(Consumer<Integer> consumer) { for (int i = 0; i < size; i++) { //System.out.println(array[i]); //提供array[i],不需要返回值 consumer.accept(array[i]); } } //遍历数组2 迭代器模式 @Override public Iterator<Integer> iterator() { //匿名内部类 return new Iterator<Integer>() { int i = 0; @Override public boolean hasNext() { //有没有下一个元素 return i < size; } @Override public Integer next() { //返回当前元素,并将指针移向下一个元素 return array[i++]; } }; } //遍历数组3 数据流 public IntStream stream() { return IntStream.of(Arrays.copyOfRange(array, 0, size)); } public int remove(int index) { int removeed = array[index]; System.arraycopy(array, index + 1, array, index, size - index - 1); size--; return removeed; } } }
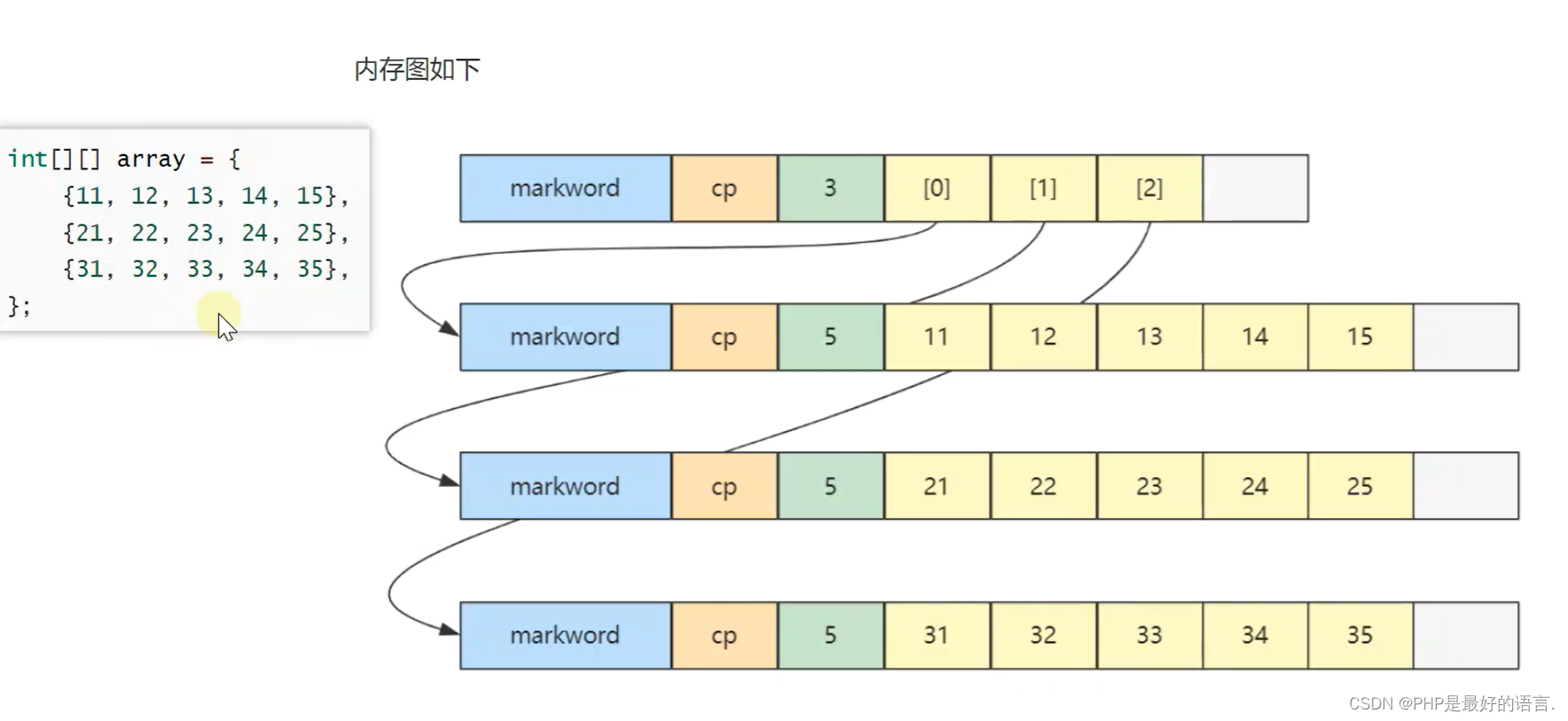
2.4 二维数组
(1)二维数组占32个字节,其中array[0],array[1],array[2]元素分别保存了指向三个一维数组的引用。
(2)三个一维数组各占40个字节。
(3)他们在内存布局上是连续的。
package org.alogorithm.array; public class Main03 { public static void main(String[] args) { int rows = 1_000_000; int columns = 14; int[][] arr = new int[rows][columns]; long ijStar = System.currentTimeMillis(); ij(arr, rows, columns); long ijEnd = System.currentTimeMillis(); System.out.println("ij执行时间为:"+(ijEnd-ijStar));//ij执行时间为:10 long jiStar = System.currentTimeMillis(); ji(arr, rows, columns); long jiEnd = System.currentTimeMillis(); System.out.println("ji执行时间为:"+(jiEnd-jiStar));//ji执行时间为:47 } public static void ji(int[][] arr, int rows, int columns) { int sum = 0; for (int j = 0; j < columns; j++) { for (int i = 0; i < rows; i++) { sum += arr[i][j]; } } System.out.println(sum+"ji"); } public static void ij(int[][] arr, int rows, int columns) { int sum = 0; for (int i = 0; i < rows; i++) { for (int j = 0; j < columns; j++) { sum += arr[i][j]; } } System.out.println(sum+"ij"); } }在计算机中,内存是分块存储的。每个内存块称为一个页(page)。当程序访问数组时,CPU会从内存中加载包含该元素所在的整个页面到高速缓存(cache)中。
在这个例子中,ij和ji两个方法的主要区别在于它们遍历数组的方式:
ij按行遍历数组:它首先遍历所有的行,然后在同一行内遍历列。
ji按列遍历数组:它先遍历所有的列,然后在同一列内遍历行。
由于现代计算机体系结构的设计特点,ij比ji更快的原因有以下几点:(1)缓存局部性(Cache Locality):按行遍历数组时,相邻的元素在物理内存中彼此靠近,这使得CPU可以高效地利用缓存来加速数据访问。这是因为通常情况下,一次内存读取操作将加载一整块数据(通常是64字节),如果这一块数据中的多个元素被连续使用,那么这些元素很可能都在同一块缓存中,从而减少了对主内存的访问次数。
(2)预取(Prefetching):一些现代处理器具有预取机制,可以预测接下来可能需要的数据并提前将其加载到缓存中。按照行顺序遍历数组时,这种机制更有可能发挥作用,因为相邻的元素更可能在未来被访问。
综上所述,ij的遍历方式更适合计算机硬件的工作原理,因此执行速度更快。
完。。