文章目录
- 一、归并排序
- 1、概念
- 2、过程
- 3、代码实现
- 4、复杂度
- 5、稳定性
- 二、 计数排序
- 1、思路
- 2、代码实现
- 3、复杂度:
- 4、稳定性
一、归并排序
1、概念
是建立在归并操作上的一种有效,稳定的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
2、过程
假设前提:
左半区间 ->有序
右半区间 ->有序
怎么使左右排序呢?
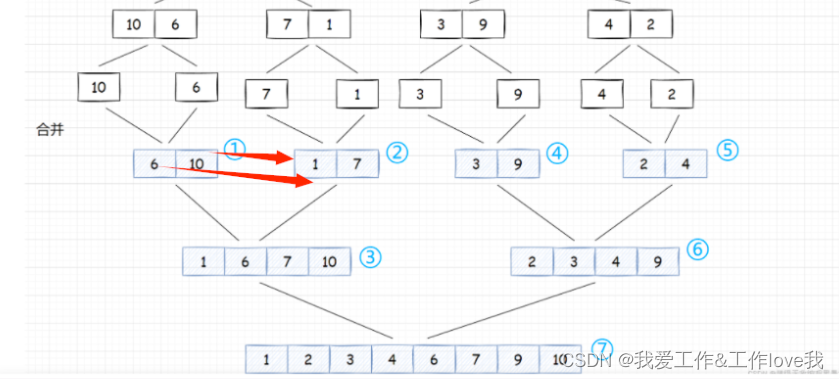
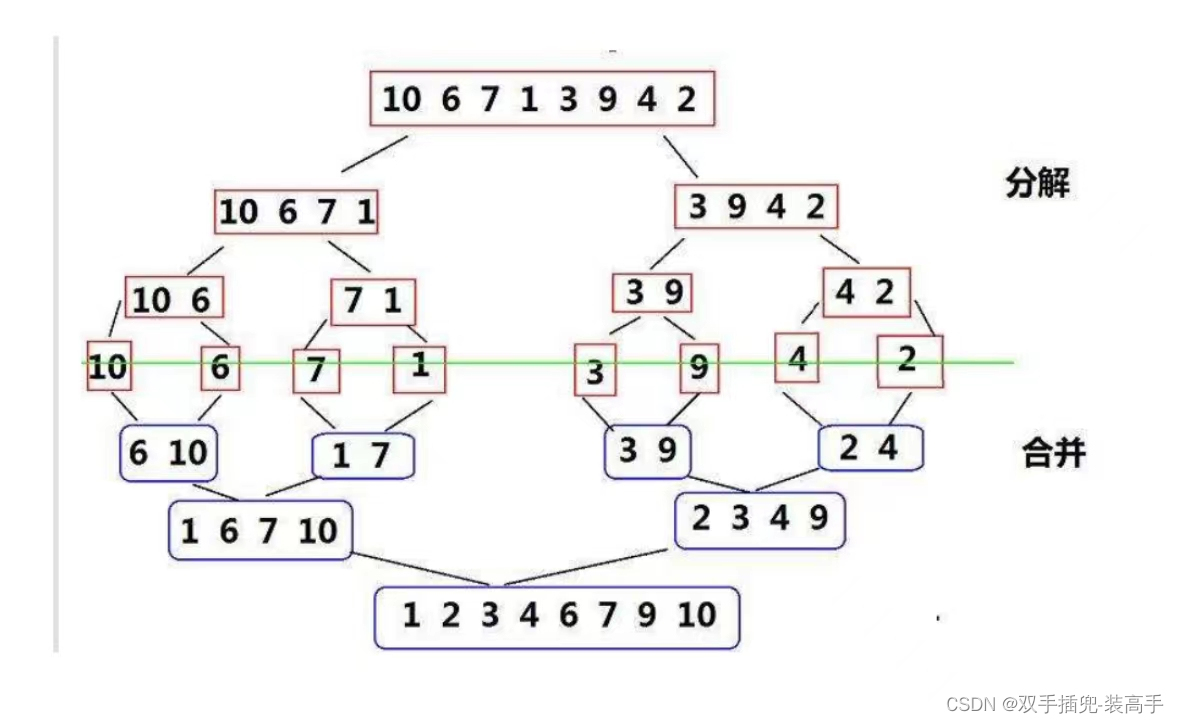
当只剩下一个元素时我们可以默认其为有序的,所以我们可以利用递归将数组中的元素划分为一个,再两组两组合并,以此类推。
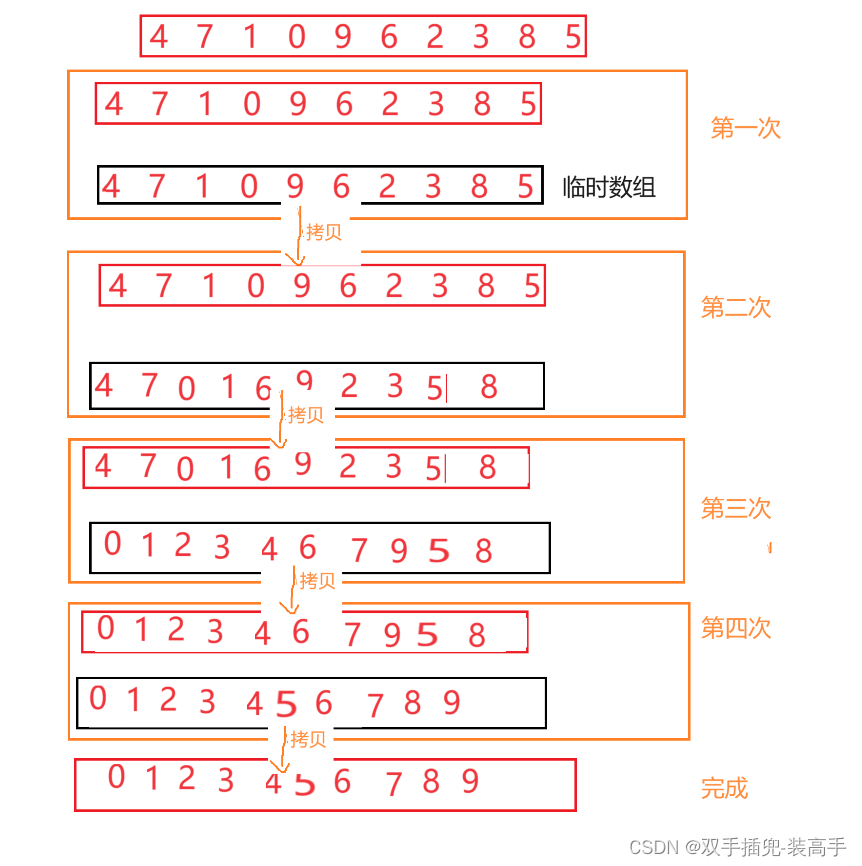
归并,依次对比取小的放到新到临时数组中,完成排序后再将临时数组的数据拷贝回原来的数组
过程图:
3、代码实现
递归:
void Print(int* arr, int n) {
for (int i = 0; i < n; i++)
printf("%d ", arr[i]);
}
//递归
void _MergeSort(int *a,int *t,int left,int right) {
//结束条件
if (left >= right)
return;
int mid = (left + right) >> 1;//取中间数,划分区间
//[left mid] [mid+1 right]
//递归
_MergeSort(a, t, left, mid);
_MergeSort(a, t, mid + 1, right);
//回归
int begin1 = left, end1 = mid;//左区间
int begin2 = mid + 1 , end2 = right;//右区间
//临时数组下标->对应的是数组a的下标
int index = left;
//当左区间或者右区间,遍历完了就结束了
while (begin1 <= end1 && begin2 <= end2) {
//选择小的放进临时数组
if (a[begin1] < a[begin2])
t[index++] = a[begin1++];
else
t[index++] = a[begin2++];
}
//判断左右两边是否都空了,不为空将后面补上
while (begin1 <= end1)
t[index++] = a[begin1++];
while (begin2 <= end2)
t[index++] = a[begin2++];
//最后拷贝回去
for (int i = left; i <= right; ++i)
a[i] = t[i];
}
void MergeSort(int* a, int n) {
int* t = (int*)malloc(sizeof(int) * n);
_MergeSort(a, t, 0, n - 1);
free(t);
}
int main() {
int a[] = { 3,7,1,0,9,6,2,3,8,5 };
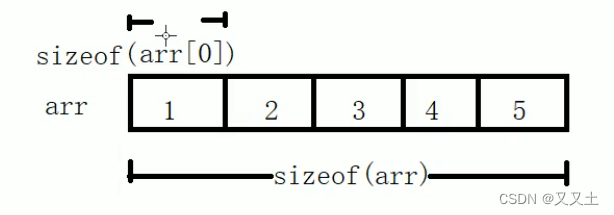
MergeSort(a, sizeof(a) / sizeof(a[0]));
Print(a, sizeof(a) / sizeof(a[0]));
return 0;
}
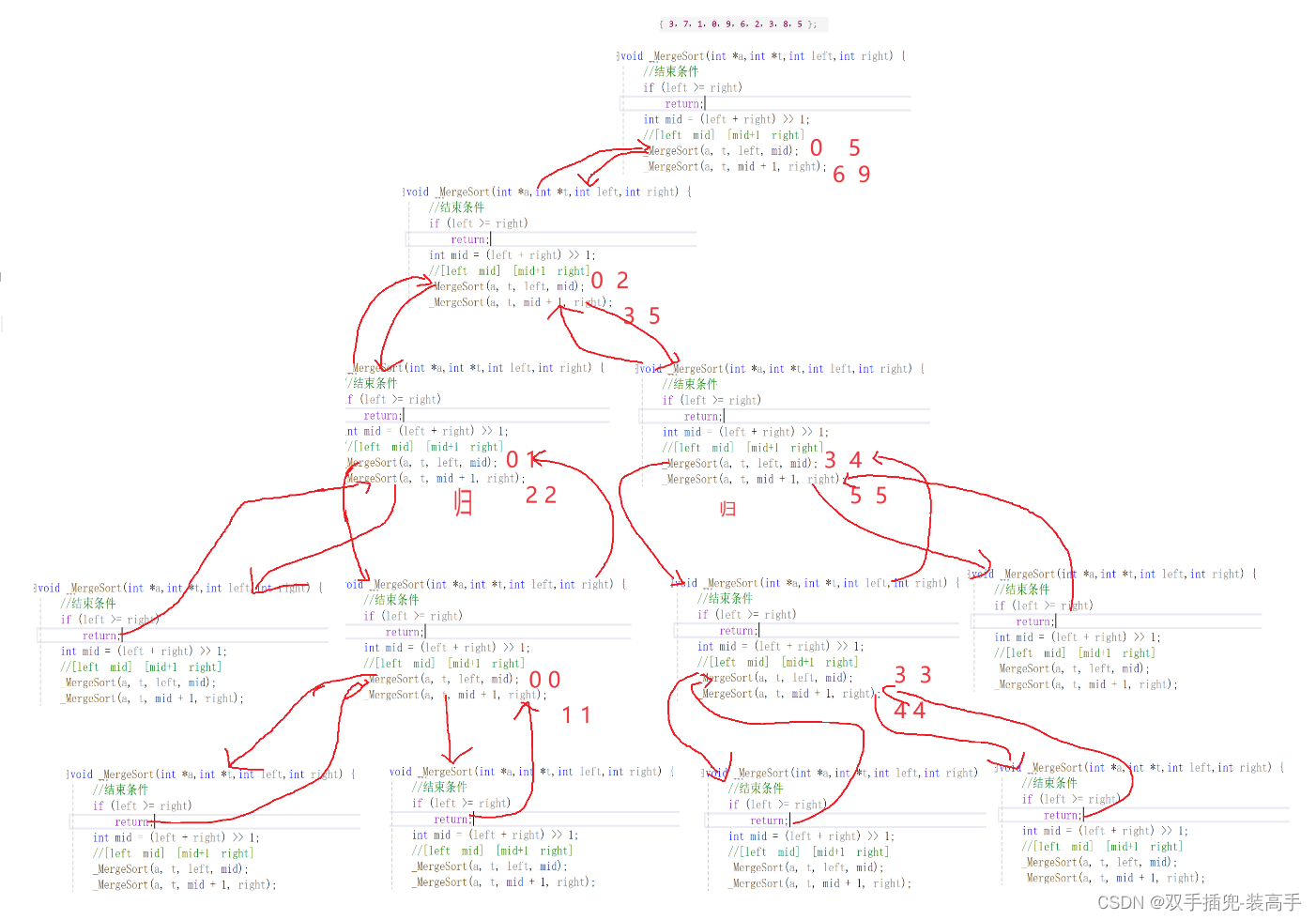
递归图(左边,先递后归):
非递归:
我们通过循环来实现非递归
(1)设置一个gap来划分归并个数,先设置gap=1,这样控制第一次是两个数合并,gap再乘2,来递增,当 gap>n(数组大小)时结束
(2)在合并的过程中可能出现两种情况
a.合并过程中右边没元素
如:

解决办法:因为已经排好了,直接打破循环即可
b,右边有元素但是不够
如:
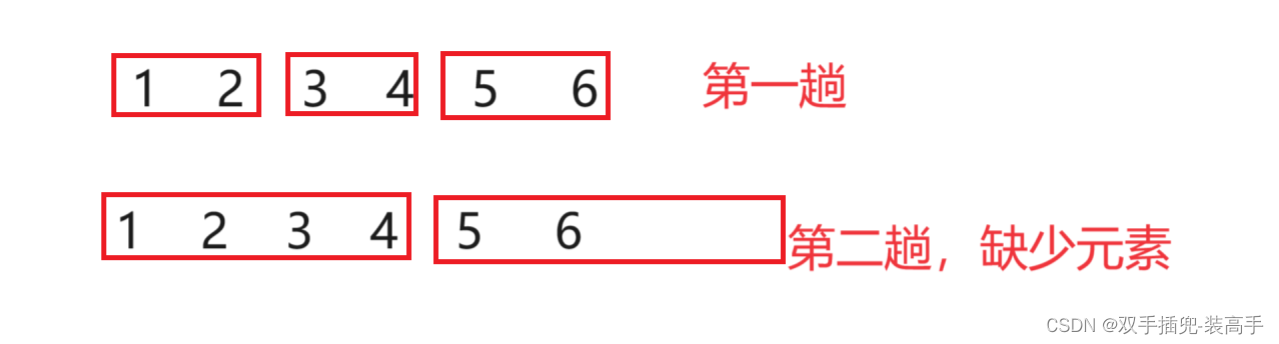
解决办法:进行纠正,将右端的下标改为 n-1(数组大小-1)
代码实现:
//非递归
void MergeSortNonR(int* a, int* t,int n) {
int gap= 1;//划分一次归并多少个元素
//结束条件
while (gap<n) {
for (int i = 0; i < n; i += 2*gap) {
//通过gap划分区间
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + gap * 2 - 1;
//情况a,此时直接打破即可
if (begin2 >= n)
break;
//情况b,进行纠正
if (end2 >= n)
end2 = n - 1;
int index = i;//从控制的区间最小的位置开始
//下面过程与递归过程一样
while (begin1 <= end1 && begin2 <= end2) {
if (a[begin1] < a[begin2])
t[index++] = a[begin1++];
else
t[index++] = a[begin2++];
}
while (begin1 <= end1)
t[index++] = a[begin1++];
while (begin2 <= end2)
t[index++] = a[begin2++];
for (int j = i; j <= end2; j++)
a[j] = t[j];
}
gap *= 2;//每次加倍
}
}
void MergeSort(int* a, int n) {
int* t = (int*)malloc(sizeof(int) * n);
MergeSortNonR(a, t, n);
free(t);
}
int main() {
int a[] = { 6,3,7,1,9,5,2,8,0,4 };
MergeSort(a, sizeof(a) / sizeof(a[0]));
Print(a, sizeof(a) / sizeof(a[0]));
return 0;
}
4、复杂度
时间复杂度:
(1)循环部分:N
(2)递归部分:因为每次都减半所以就是logN(以2为底)
所以时间复杂度为:O(N*logN)
空间复杂度:
因为要重新开辟一个数组,所以空间复杂度为O(N)
5、稳定性
在归并过程中相同的元素的顺序不会发生改变,所以是稳定的
二、 计数排序
1、思路
通过映射统计每个数出现的次数,再使用次数排序
如:

上述是以最大数去创建空间
但是如果遇到一个很大的数的话就需要我们创建空间时就会很浪费
如:
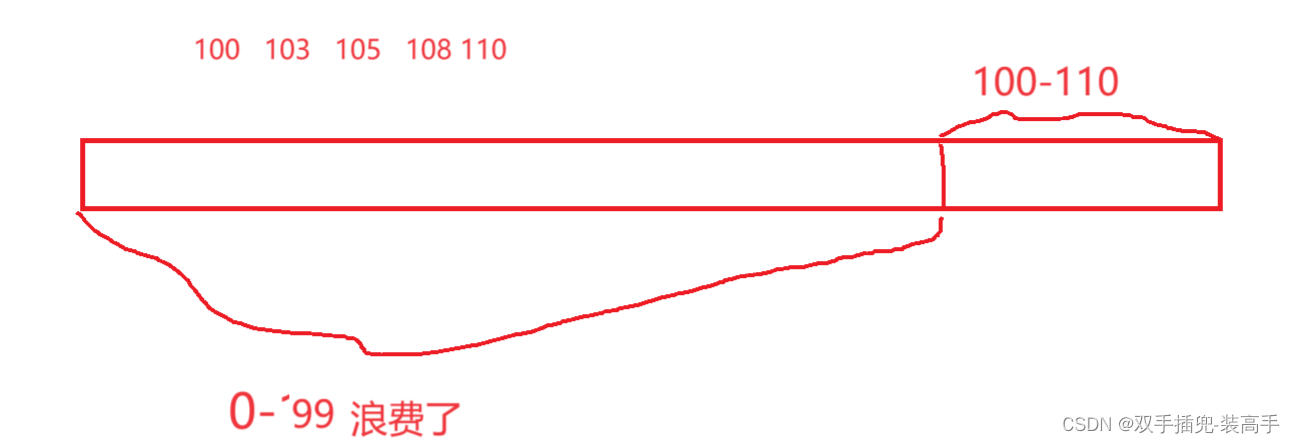
解决:找到范围,使用范围+1去创建临时空间
2、代码实现
//计数排序
void CountSort(int* a, int n) {
int max = a[0];
int min = a[0];
//求出数组的范围
for (int i = 0; i < n; i++) {
if (max < a[i])
max = a[i];
if (min > a[i])
min = a[i];
}
int t = max - min+1;
//临时空间
int* p = (int*)calloc(t,sizeof(int));
//统计个数
for (int j = 0; j < n; j++) {
//a[j]-min当下标,我们下次直接加回min即可
p[a[j] - min]++;
}
int i = 0;
//按顺序拷贝回原来的数组
for (int j = 0; j < t; j++) {
while (p[j]) {
a[i] = j + min;
i++;
p[j]--;
}
}
free(p);
p = NULL;
}
3、复杂度:
空间复杂度:因为要创建临时的空间,所以复杂度为O(N);
时间复杂度:O(N+t)
4、稳定性
在统计和重新排序过程中相同元素可能位置发生交换,所以为不稳定
以上就是我的分享了,如果有什么错误,欢迎在评论区留言。
最后,谢谢大家的观看!