1311:【例2.5】求逆序对
【题目描述】
给定一个序列a1,a2,…,an,如果存在i<j并且ai>aj,那么我们称之为逆序对,求逆序对的数目。
【输入】
第一行为n,表示序列长度,接下来的n行,第i+1行表示序列中的第i个数。
【输出】
所有逆序对总数
【输入样例】
4
3
2
3
2
【输出样例】
3
【提示】
N≤105,Ai≤105
注意:
-
逆序数的可以考虑是排序过程时大数在前小数在后的比较次数,如果数组比较大则不能考虑冒泡、选择、插入(时间复杂度很高)
-
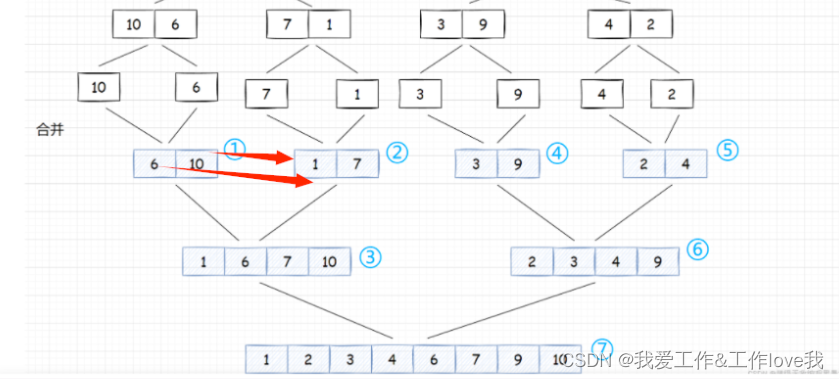
逆序数由于在递归排序时是中间偏后一位的数和之前的作比较,比较时只要第一位比它大则剩下的左序列都比他大,所以逆序数一次可求多个(冒泡一次交换只能得到一个逆序数对):
num+=mid-i+1
-
由于数组比较大时,逆序数这个值可能很大,需要数据类型为
long long
代码:
#include <bits/stdc++.h>
using namespace std;
const int Max = 100011;
int a[Max],r[Max];
long long num=0;
void merge_sort(int s,int t);
int main(){
int len;
cin>>len;
for(int i=0;i<len;i++){
cin>>a[i];
}
merge_sort(0,len-1);
cout<<num;
return 0;
}
void merge_sort(int s,int t){
if(s==t) return ;
int mid = (s+t)/2;
merge_sort(s,mid);//先完成左边的排序
merge_sort(mid+1,t);//先再完成右边的排序
int i=s,j=mid+1,k=s;//开始合并序列
while(i<=mid&&j<=t){//将数据放到临时数组里面,判断的左边的序列右边子序列的第一个(即mid+1)
if(a[i]<=a[j]){ //判断是否该值小于右边子序列的第一个值
r[k]=a[i];
k++,i++;
}else{
r[k]=a[j]; //否则较小的值就移到临时数组K
num+=mid-i+1;
k++,j++;
}
}
while(i<=mid){ //复制左边的剩下序列过去
r[k]=a[i];
k++,i++;
}
while(j<=t){ //复制右边的序列
r[k]=a[j];
k++,j++;
}
for(int i=s;i<=t;i++){
a[i]=r[i]; //将此次排序的数据放回数组中
cout<<a[i]<<" ";
}
cout<<endl;
}