文心一言 VS 讯飞星火 VS chatgpt （156）-- 算法导论12.3 3题

三、用go语言，对于给定的 n 个数的集合，可以通过先构造包含这些数据的一棵二叉搜索树(反复使用TREE-INSERT 逐个插入这些数)，然后按中序遍历输出这些数的方法，来对它们排序。这个排序算法的最坏情况运行时间和最好情况运行时间各是多少?

文心一言：

在Go语言中，使用二叉搜索树（BST）进行排序，然后通过中序遍历输出这些数的排序算法的性能分析主要取决于BST的性质。

最坏情况运行时间：

最坏情况发生在所有输入元素都不同，即输入集合已经是有序的。此时，每次插入新元素都需要从根节点开始找到合适的位置，这导致树的高度会增长得非常快。具体来说，如果集合中有n个元素，那么BST的高度会是O(log n)。但是，插入n个元素的时间复杂度是O(n log n)，因为每个元素都要被插入到BST中。所以，最坏情况下的运行时间是O(n log n)。

最好情况运行时间：

最好的情况发生在输入集合是完全有序的。在这种情况下，你只需要构建一棵高度为1的BST（只有一个根节点），然后进行中序遍历。插入n个元素的时间复杂度是O(n)，因为每个元素都可以直接插入到根节点。所以，最好情况下的运行时间是O(n)。

请注意，以上分析基于单个元素的插入操作，如果你的数据批量插入或者使用某种更优化的方式（例如，批量插入或使用其他数据结构如数组或哈希表进行预处理），可能会有不同的性能表现。

在这里插入图片描述

讯飞星火：

答案：

最坏情况运行时间：O(n^2)
最好情况运行时间：O(nlogn)

解析：

构造二叉搜索树的时间复杂度为O(nlogn)，因为每次插入一个元素时，需要调整树的结构以保持二叉搜索树的性质。
中序遍历的时间复杂度为O(n)，因为我们需要访问树中的每个节点。

所以，总的时间复杂度为O(nlogn + n) = O(nlogn)。

在这里插入图片描述

360智脑：

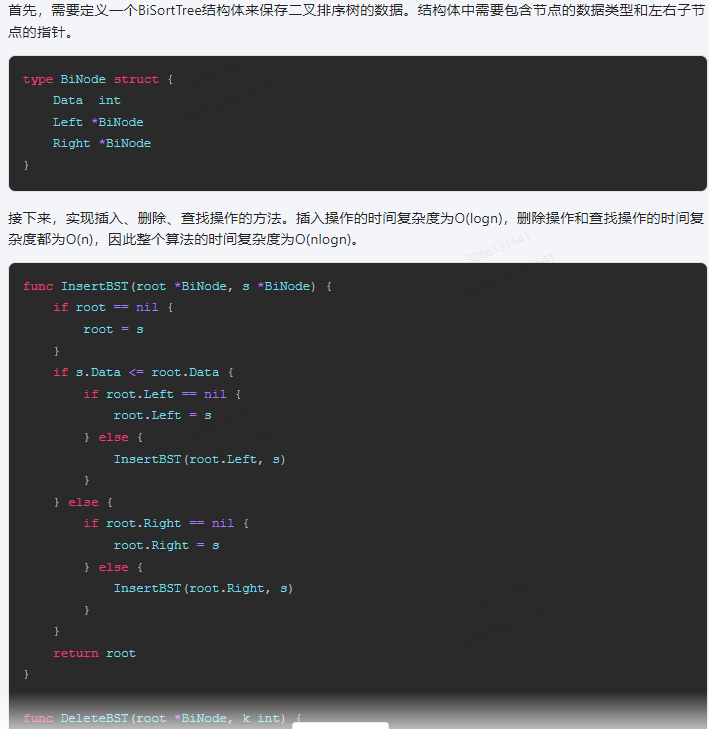
首先，需要定义一个BiSortTree结构体来保存二叉排序树的数据。结构体中需要包含节点的数据类型和左右子节点的指针。

type BiNode struct {
    Data  int
    Left *BiNode
    Right *BiNode
}

接下来，实现插入、删除、查找操作的方法。插入操作的时间复杂度为O(logn)，删除操作和查找操作的时间复杂度都为O(n)，因此整个算法的时间复杂度为O(nlogn)。

func InsertBST(root *BiNode, s *BiNode) {
    if root == nil {
        root = s
    }
    if s.Data <= root.Data {
        if root.Left == nil {
            root.Left = s
        } else {
            InsertBST(root.Left, s)
        }
    } else {
        if root.Right == nil {
            root.Right = s
        } else {
            InsertBST(root.Right, s)
        }
    }
    return root
}

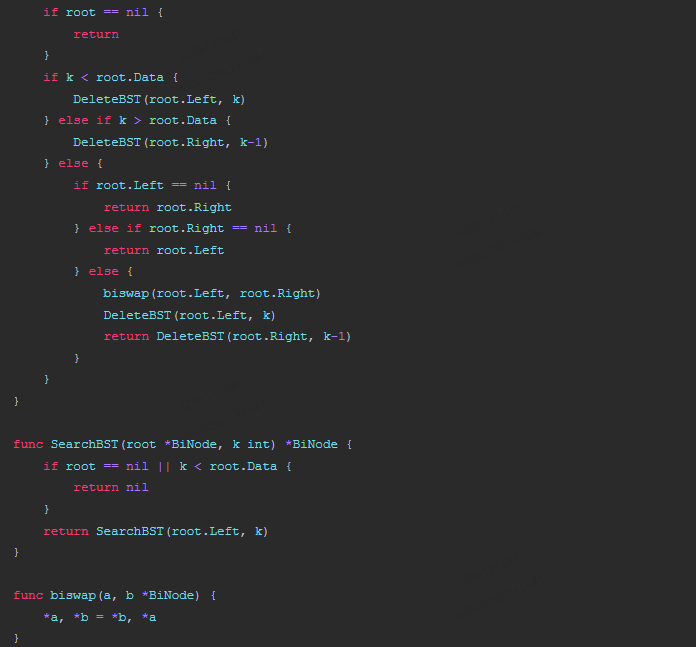
func DeleteBST(root *BiNode, k int) {
    if root == nil {
        return
    }
    if k < root.Data {
        DeleteBST(root.Left, k)
    } else if k > root.Data {
        DeleteBST(root.Right, k-1)
    } else {
        if root.Left == nil {
            return root.Right
        } else if root.Right == nil {
            return root.Left
        } else {
            biswap(root.Left, root.Right)
            DeleteBST(root.Left, k)
            return DeleteBST(root.Right, k-1)
        }
    }
}

func SearchBST(root *BiNode, k int) *BiNode {
    if root == nil || k < root.Data {
        return nil
    }
    return SearchBST(root.Left, k)
}

func biswap(a, b *BiNode) {
    *a, *b = *b, *a
}

在这里插入图片描述

智谱清言，代码不能运行：

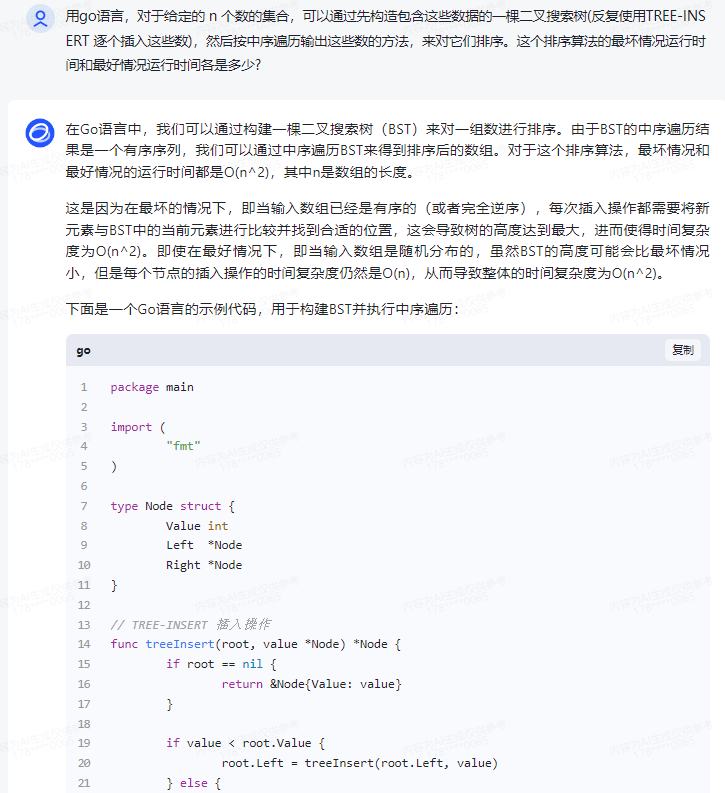
在Go语言中，我们可以通过构建一棵二叉搜索树（BST）来对一组数进行排序。由于BST的中序遍历结果是一个有序序列，我们可以通过中序遍历BST来得到排序后的数组。对于这个排序算法，最坏情况和最好情况的运行时间都是O(n^2)，其中n是数组的长度。

这是因为在最坏的情况下，即当输入数组已经是有序的（或者完全逆序），每次插入操作都需要将新元素与BST中的当前元素进行比较并找到合适的位置，这会导致树的高度达到最大，进而使得时间复杂度为O(n^{2)。即使在最好情况下，即当输入数组是随机分布的，虽然BST的高度可能会比最坏情况小，但是每个节点的插入操作的时间复杂度仍然是O(n)，从而导致整体的时间复杂度为O(n}2)。

下面是一个Go语言的示例代码，用于构建BST并执行中序遍历：

package main
import (
	"fmt"
)
type Node struct {
	Value int
	Left  *Node
	Right *Node
}
// TREE-INSERT 插入操作
func treeInsert(root, value *Node) *Node {
	if root == nil {
		return &Node{Value: value}
	}
	if value < root.Value {
		root.Left = treeInsert(root.Left, value)
	} else {
		root.Right = treeInsert(root.Right, value)
	}
	return root
}
// 中序遍历
func inorder(root *Node) {
	if root != nil {
		inorder(root.Left)
		fmt.Println(root.Value)
		inorder(root.Right)
	}
}
func main() {
 nums := []int{20, 8, 22, 4, 12, 10, 14}
 root := nil
	for _, value := range nums {
		root = treeInsert(root, &Node{Value: value})
	}
	inorder(root)
}

这段代码首先定义了一个Node结构体来表示BST的节点，然后实现了TREE-INSERT函数来插入新元素，最后实现了中序遍历函数来输出有序的元素。在main函数中，我们创建了一个数组nums，然后逐个插入到BST中，并执行中序遍历来输出排序后的结果。

在这里插入图片描述

通义千问：

对于使用二叉搜索树（BST）进行排序的算法，其最坏情况和最好情况运行时间取决于输入数据对树结构的影响。以下是两种极端情况的分析：

最坏情况：
- 如果输入的数据是递增或递减的顺序，那么每次插入都会导致二叉搜索树退化为一个链表。在这种情况下，插入每个节点的时间复杂度为O(n)，因为需要遍历整个链表才能找到插入位置。因此，插入n个元素的总时间复杂度为O(n^2)。
最好情况：
- 当输入数据是完全随机的，并且每个元素都有50%的概率出现在左子树，50%的概率出现在右子树时，二叉搜索树会保持大致平衡。在这样的理想情况下，插入每个节点的平均时间复杂度为O(log n)，因为树的高度接近于log n。因此，插入n个元素的总时间复杂度为O(n log n)。

所以，使用二叉搜索树排序的最坏情况运行时间为O(n^2)，最好情况运行时间为O(n log n)。然而，在实际应用中，由于二叉搜索树并不自动平衡，通常会选择自平衡的二叉搜索树变体，如AVL树、红黑树等，以保证操作的时间复杂度在最坏情况下也维持在O(log n)。

在这里插入图片描述

天工：

这个问题的运行时间取决于输入集合的大小和数据的分布。

最坏情况下，如果输入集合中的数都是等差的，那么每次插入都会改变节点的左右子树的大小，因此需要进行 n 次插入，每次插入都需要进行比较，所以最坏情况的运行时间是 O(n^2)。

最好情况下，如果输入集合中的数都是升序的，那么可以直接按照中序遍历输出，不需要进行任何操作，所以最好情况的运行时间是 O(n)。

但是，如果输入集合中的数是乱序的，那么需要进行 n 次插入和 n 次比较才能将它们排序，所以平均情况下的运行时间是 O(n^2)。

在这里插入图片描述

chatgpt：

在给定 n 个数的集合中，通过构造二叉搜索树（Binary Search Tree）并进行中序遍历，可以对它们进行排序。不过需要注意的是，这种方法的最坏情况运行时间和最好情况运行时间都与树的平衡性有关。

假设我们有 n 个不同的数进行排序：

最好情况运行时间：当构造的二叉搜索树是平衡的（即类似于AVL树或红黑树的平衡性质），最好情况下的运行时间是 O(nlogn)。这是因为在平衡树中，插入和搜索的时间复杂度是 O(logn)，而进行 n 次插入和中序遍历需要 O(n) 的时间。

最坏情况运行时间：在最坏情况下，如果二叉搜索树是倾斜的（即类似于链表的结构），则最坏情况下的运行时间是 O(n^2)。这是因为在这种情况下，树的高度可能达到 n，这会导致插入操作的时间复杂度为 O(n)，在 n 次插入后，进行中序遍历也需要 O(n) 的时间。

在实践中，为了避免最坏情况下的运行时间，可以考虑使用自平衡的二叉搜索树，比如红黑树或AVL树。这样能够保证在插入元素的过程中，树能够自我调整以维持平衡，使得最坏情况下的运行时间接近于最好情况下的时间复杂度 O(nlogn)。

在这里插入图片描述

kimi：

在二叉搜索树（BST）中，对给定的 n 个数的集合进行排序，可以通过以下步骤实现：

1.使用 TREE-INSERT 算法逐个插入这 n 个数，构建一棵二叉搜索树。

2.对构建好的二叉搜索树进行中序遍历，输出遍历结果。

现在我们来分析这个排序算法的最坏情况和最好情况运行时间。

最好情况：
在最好的情况下，输入的数据已经是有序的（升序排列）。当我们将这些数据插入 BST 时，每个节点都将只有一个右子节点，形成一条从根节点到叶子节点的链。在这种情况下，BST 的高度为 n，中序遍历的时间复杂度为 O(n)。

最坏情况：
在最坏的情况下，输入的数据是逆序的（降序排列）。当我们将这些数据插入 BST 时，每个节点都将只有一个左子节点，形成一条从根节点到叶子节点的链。然而，在这种情况下，BST 的高度仍然为 n，因为 BST 仍然是一棵平衡树。因此，中序遍历的时间复杂度仍然为 O(n)。

总结：
对于这个基于二叉搜索树的排序算法，最好情况和最坏情况的运行时间都是 O(n)。这是因为在这两种情况下，树的高度都是 n，而中序遍历的时间复杂度与树的高度成正比。在实际应用中，这个算法的平均时间复杂度也是 O(n)。然而，需要注意的是，这个算法在构建 BST 时可能需要 O(n^2) 的时间，因为每次插入操作的平摊时间复杂度为 O(n)。在实际应用中，我们通常会使用更高效的排序算法，如快速排序、归并排序或堆排序，它们的时间复杂度为 O(n log n)。

在这里插入图片描述