差分进化算法DE

news2024/9/28 7:24:04

此算法是一种基于贪心的并行直接搜索算法。

1.过程

（1）初始化种群

NP个D维的参数向量 $x_{i,g}$ (i=1,2,...,NP)作为每一代G种群，种群规模必须>=4

（2）变异

使用种群中两个不同向量来干扰一个现有向量，进行差分操作，实现变异。变异时需要确保变异向量不会超出边界，若超出则需要进行修正。F为变异因子∈[0,2]，控制差分变化的放大倍数。

对于每个目标向量 $x_{i,G}$ 都要根据三个不同向量生成一个变异向量 $v_{i,G+1}$

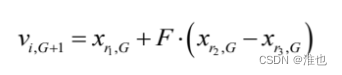
（3）交叉

每个个体和它生成的子代变异向量进行交叉，每个分量按一定的概率选择子代变异向量来生成试验个体，若没有选择子代变异向量则此分量为原个体的分量。按照上述方法生成试验向量 $u_{i,j}(g)$ 。CR为交叉概率因子；jrand是[1,...,D]中随机选择的索引，确保u从v获得至少一个分量。

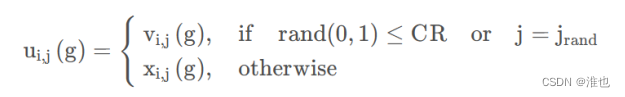
（4）选择

根据贪婪原则，如果试验向量成本函数值<目标向量成本函数值，则下一代的种群个体设置为试验向量，否则保留上一代的目标向量。

2、流程图

3、代码

from random import random
from random import sample
from random import uniform
import matplotlib.pyplot as plt
import matplotlib
matplotlib.use('TkAgg')

# 向量维度的平方求和
def sphere(x):
    total = 0
    for i in range(len(x)):
        total += x[i]**2
    return total

# 确保变异向量不超出边界
def ensure_bounds(vec, bounds):
    vec_new = []
    # 遍历变异向量的每个维度
    for i in range(len(vec)):
        # 变量比边界最小值还小，赋值为边界最小值
        if vec[i] < bounds[i][0]:
            vec_new.append(bounds[i][0])
        # 变量比边界最大值还大，赋值为边界最大值
        if vec[i] > bounds[i][1]:
            vec_new.append(bounds[i][1])
        # 变量满足边界条件，不进行操作
        if bounds[i][0] <= vec[i] <= bounds[i][1]:
            vec_new.append(vec[i])
    return vec_new


# ——————————————————————————DE————————————————————————————————

def minimize(bounds, popsize, mutate, recombination, maxiter):
    # 种群初始化

    population = []     # 空的种群
    gen_avg_record = []     # 适应度平均值
    gen_best_record = []        #适应度最优值
    for i in range(0, popsize):
        indv = []
        for j in range(len(bounds)):    # D=2，所以j取0,1
            indv.append(uniform(bounds[j][0], bounds[j][1]))     # uniform 均匀分布
        population.append(indv)     # append 追加

    # 进行迭代

    for i in range(1, maxiter+1):
        print("generation:", i)     #输出种群
        gen_scores = []

        for j in range(0, popsize):
            # 变异
            candidates = list(range(0, popsize))
            candidates.remove(j)    # 去除目标向量的序号
            random_index = sample(candidates, 3)    # 从candidates中随机抽取除3个元素
            x_1 = population[random_index[0]]   # 抽到2，则选取种群中第二个个体作为x_r1g
            x_2 = population[random_index[1]]
            x_3 = population[random_index[2]]
            x_t = population[j]     # 目标向量

            # x_r2g减x_r3g，生成新向量 x_diff
            # zip(numbers, letters) 生成 (x, y) 形式的元组的迭代器,x取自数字.y取自字母
            x_diff = [x_2_i - x_3_i for x_2_i,x_3_i in zip(x_2, x_3)]

            # 变异向量 v_ig+1 = x_r1g +F * (x_r2g - x_r3g)
            v_donor = [x_1_i + mutate * x_diff_i for x_1_i, x_diff_i in zip(x_1, x_diff)]
            # 确保变异向量在边界内
            v_donor = ensure_bounds(v_donor, bounds)

            # 交叉
            v_trial = []    # 试验向量
            for k in range(len(x_t)):
                crossover = random()    # 生成[0,1]内的随机数
                if crossover <= recombination:
                    v_trial.append(v_donor[k])
                else:
                    v_trial.append(x_t[k])

            # 选择
            score_trial = sphere(v_trial)   # sphere：向量各个维度的平方和
            score_target = sphere(x_t)

            if score_trial < score_target:
                population[j] = v_trial
                gen_scores.append(score_trial)
                print(">", score_trial, v_trial)
            else:
                print(">", score_target, x_t)
                gen_scores.append(score_target)

        gen_avg = sum(gen_scores) / popsize
        gen_best = min(gen_scores)
        gen_avg_record.append(gen_avg)
        gen_best_record.append(gen_best)
        gen_sol = population[gen_scores.index(min(gen_scores))]

        print("，种群平均值：", gen_avg)
        print("，种群最优值：", gen_best)
        print("，最好结果：", gen_sol)

        pass

    # 画图
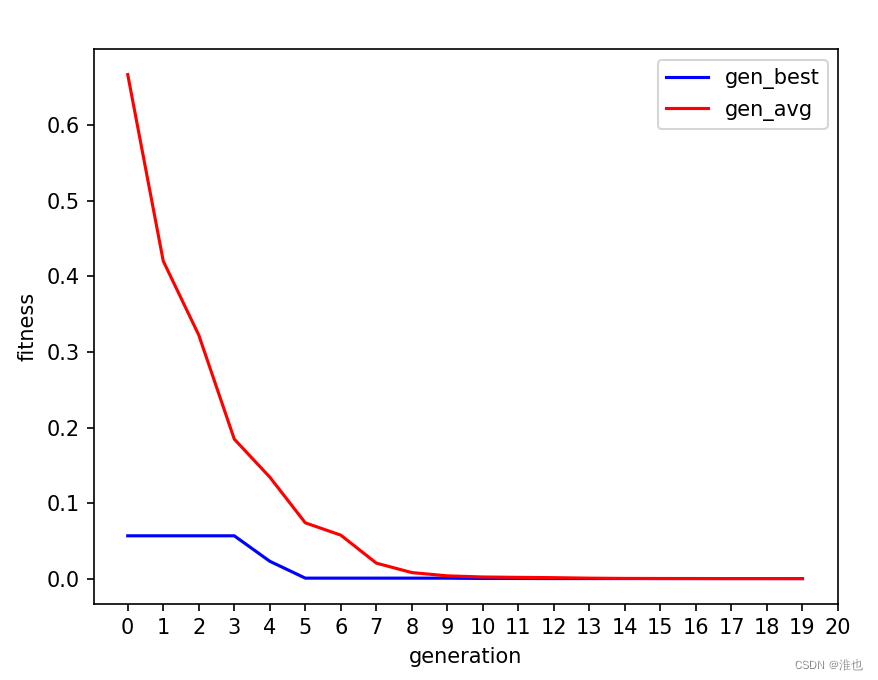
    plt.plot([i for i in range(len(gen_best_record))], gen_best_record, 'b')
    plt.plot([i for i in range(len(gen_avg_record))], gen_avg_record, 'r')
    plt.ylabel('fitness')
    plt.xlabel('generation')
    plt.yticks([0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6])  # 设置y轴刻度
    plt.xticks([0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20])  # 设置x轴刻度
    plt.legend(['gen_best', 'gen_avg'])
    plt.show()

#设置参数
bounds = [(-1,1),(-1,1)]    # 维度D=2,搜索空间范围也叫约束边界
popsize = 10    # 种群规模NP
mutate = 0.5    # 变异因子 F
recombination = 0.7    # 交叉概率 CR [0,1]
maxiter = 20    # 最大迭代次数
# DE/rand/1/bin
minimize(bounds, popsize, mutate, recombination, maxiter)