代码：

class Solution {
    public int findPeakElement(int[] nums) {
        int left=0,right=nums.length-1;
        while (left<right){
            int mid=left+(right-left)/2;

            if(nums[mid]>nums[mid+1]){
                right=mid;
            }else {
                left=mid+1;
            }
        }

        return left;
    }
}

题解：

        通过题意进行分析我们知道

        1.数组中有多个峰值，我们只需要找出其中的一个即可

        2. nums[-1] = nums[n] = -∞ 

        我们可以做出如下的图示：

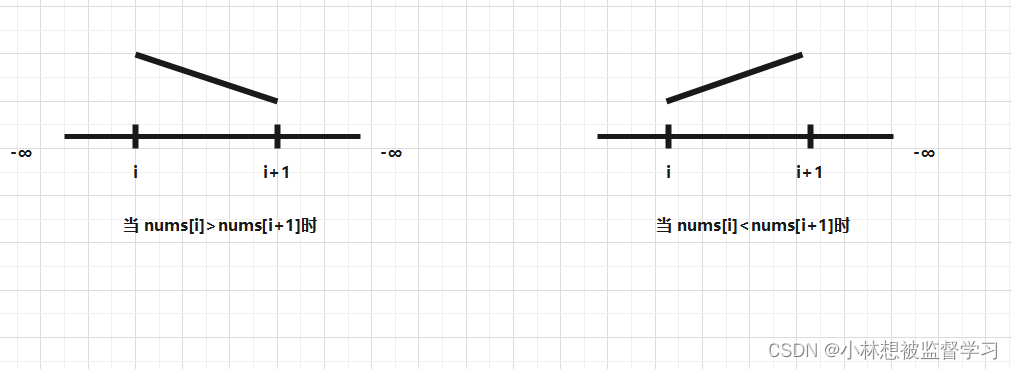        当 nums[i]>nums[i+1]时，i 下标的左边肯定存在一个峰值，因为最左边是 - ∞ ，所以必定需要经历递增，再在 i 这里经历递减，所以必定存在一个峰值，但 i 的右边，可能不会存在峰值，因为可以直接递减到 - ∞，所以我们可以大胆的去除掉 i 右边的数据（i 下标指向的数据不能去除，因为我们不确定 i 是否就是要找的峰值）

         当 nums[i] < nums[i+1]时，i 下标的右边肯定存在一个峰值，但 i 的左边，可能不会存在峰值，所以我们可以大胆的去除掉 i 左边的数据和 i 的值

        根据上述的分析，我们知道该题具有二段性，所以我们可以通过二分法来解决该问题，因为 nums[i]>nums[i+1]时 i 指针指向的数据才可能满足要求，所以相当于我们要找递减情况下的左边界

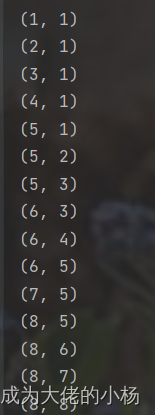
        通过示例1来进行分析：

输入：nums = [1,2,3,1]

        L 和 R 指针指向数组的两端，计算 mid = L+（R - L）/2 = 1,此时 nums[mid] < nums[mid+1]，我们可以大胆去除 mid 及其 mid 左边的数据，让 L= mid+1

1        2        3        1

L       mid               R

        计算此时的中点 mid = 2，此时 nums[mid] > nums[mid+1] ,我们可以大胆去除 mid 右边的数据（不能去除 mid 指向的数据，因为我们不能确定 mid 指向的数据是否是我们要找的数据），让 R = mid

1        2        3        1

                    L        R

                   mid

        当 L 和 R 指针相遇时，我们便找到了需要的峰值

1        2        3        1

                    L        

                    R