这个标题涉及到主动配电网的日前-日内协同调度方法，其关键要素包括“最优经济运行区域”和“日前-日内协同调度”。

1. 主动配电网： 这指的是一种能够主动响应和参与调度的配电网系统。传统的配电网通常是被动的，即电力从电源到终端用户的传输是由系统运营商掌控的。而主动配电网能够更灵活地管理分布式能源资源、储能系统和负荷。

2. 日前-日内协同调度： 这表示调度方法考虑了两个不同的时间尺度，即日前和日内。日前调度通常指的是对未来24小时内的电力需求和供给进行规划，而日内调度则是在实际运行过程中对电力系统进行更短时间内的调整。协同调度强调这两个时间尺度之间的协同优化，以确保整体系统的高效性和可靠性。

3. 基于最优经济运行区域： 这可能指的是在调度过程中，系统考虑了经济运行区域的最优化。经济运行区域可能是指在电力系统中，能够以最经济的方式满足电力需求的一定范围或状态。通过考虑这一区域内的最优化问题，可以在经济效益和系统运行的可靠性之间找到平衡。

因此，这个标题的主题是关于如何在主动配电网中，通过考虑最优经济运行区域，制定一种协同调度方法，以在日前和日内两个时间尺度上实现电力系统的高效和可靠运行。这可能涉及到复杂的优化算法、能源管理策略以及对分布式能源资源的灵活调度。

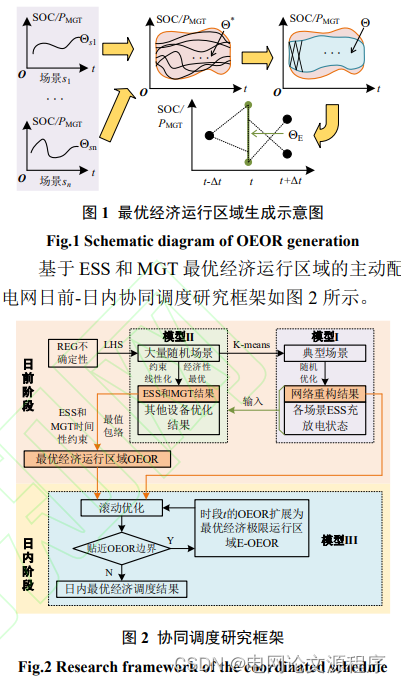
摘要：传统的日前-日内协同调度通常以与日前时序计划曲线偏差最小作为日内目标函数，当日内新能源出力预测值与日前相差较大时，储能装置（ESS）等由于其时间耦合约束日内调整范围有限，导致经济性和灵活性较差。对此，本文提出了基于最优经济运行区域（OEOR）的主动配电网（ADN）日前-日内协同调度方法。在日前阶段，构建线性化ADN调度模型，基于拉丁超立方采样法生成的大量随机场景下调控设备优化曲线，以全时间段内设备出力上下界内所包含的随机场景优化结果数量最大为目标，考虑储能装置荷电状态的相邻时段约束和微型燃气轮机的爬/滑坡率，构建OEOR生成模型。最后，在日内阶段，调控设备在OEOR内滚动优化调整，当该时段优化值贴近OEOR边界时，考虑相邻时段出力约束，将OEOR扩展为最优经济极限运行区域（E-OEOR）。算例结果表明，所提方法相比于传统方法能够更有效地提升配电网经济性。

这段摘要描述了一种基于最优经济运行区域（OEOR）的主动配电网（ADN）日前-日内协同调度方法，旨在解决传统调度中由于新能源出力预测误差导致的经济性和灵活性较差的问题。

具体解读如下：

1. 问题陈述： 传统的日前-日内协同调度通常以最小化日内时序计划曲线与实际发电情况的偏差作为目标函数。然而，当日内新能源出力预测值与日前计划相差较大时，一些设备（如储能装置）由于时间耦合的约束，其日内调整范围有限，从而影响了系统的经济性和灵活性。

2. 提出方法： 为解决上述问题，该文提出了一种基于OEOR的ADN日前-日内协同调度方法。在日前阶段，作者构建了线性化的ADN调度模型，并利用拉丁超立方采样法生成大量随机场景下的调控设备优化曲线。目标是在全时间段内设备出力上下界内包含尽可能多的随机场景，考虑储能装置荷电状态的相邻时段约束和微型燃气轮机的爬/滑坡率，构建OEOR生成模型。

3. 日内调整： 在日内阶段，调控设备在OEOR内进行滚动优化调整。当该时段的优化值接近OEOR边界时，考虑相邻时段的出力约束，将OEOR扩展为最优经济极限运行区域（E-OEOR）。

4. 结果验证： 算例结果表明，该方法相较于传统方法更有效地提升了配电网的经济性。这可能意味着通过考虑更多的随机场景和设备调整的灵活性，系统在应对日前计划与实际情况偏差时表现更为优越。

总体而言，该方法旨在提高配电网在日前-日内调度过程中的经济性和灵活性，从而更好地适应新能源等因素的不确定性。

关键词:最优经济运行区域;时间耦合性约束;协同调度;主动配电网;
 

1. 最优经济运行区域（OEOR）： 这指的是系统中一种经济性最优的运行状态或区域。在这个上下文中，可能是指在配电网中，通过考虑各种因素（如成本、效率等），确定系统在某个特定时间段内的最优运行状态或运行区域。

2. 时间耦合性约束： 这表示系统中各个组件或设备在时间上相互关联或相互依赖的约束。在电力系统中，这可能涉及到不同设备在时间上的操作和调整需要考虑彼此的关系，尤其是在日前-日内协同调度中。

3. 协同调度： 这指的是系统中不同部分之间协同工作以实现某个共同目标的调度过程。在电力系统中，日前-日内协同调度可能涉及到日前计划和日内实际运行之间的协同工作，以确保系统的稳定运行和经济性。

4. 主动配电网（ADN）： 这表示一种具有主动调度和控制能力的配电网。主动配电网通常能够灵活应对不同的运行条件和需求，可能涉及到智能化的设备和系统，以实现更高效、可靠和可持续的电力分配。

这些关键词在文中一起被使用，指向一种新的配电网调度方法，其中通过考虑经济性最优（OEOR）、时间耦合性约束、协同调度以及主动配电网的特性，来优化日前-日内的电力系统运行。这种方法的目标可能是提高系统的经济性和灵活性，尤其在面对新能源等不确定因素时。

仿真算例：

本文选取 IEEE33 节点配电网进行算例分析， 节点负荷和支路阻抗参数见文献[23]，网架结构见 附录 D 图 D1。调控设备相关参数见附录 D [4][24]。 配电网功率基准值为 10MVA，电压基准值为 12.66kV，节点电压幅值范围为 0.93p.u.~1.07p.u.。 日前PV的预测值服从标准差为10%的平均值的正 态分布，其中平均值为日前预测出力值。采用 LHS 在±3 个标准差范围内随机生成 PV 出力场景。网 络综合运行费用权重 μOP 和网络损耗权重 μL 分别 设置为 0.7 和 0.3。负荷出力和日前-日内的 PV 预 测出力如附录 D 图 D2 所示。

仿真程序复现思路：

仿真复现思路涉及以下步骤：

1. 数据收集与准备：

   • 获取 IEEE33 节点配电网的节点负载和支路阻抗参数，网架结构信息。
   • 收集调控设备相关参数和其他附录中所需的数据，如功率基准值、电压基准值、节点电压幅值范围等。

2. PV出力场景生成：

   • 根据描述中提供的信息，使用正态分布模型生成日前PV的预测值。采用平均值作为日前预测出力，标准差为平均值的10%。
   • 使用 Latin Hypercube Sampling (LHS) 方法，在±3个标准差范围内生成符合正态分布的随机数作为PV出力场景。

3. 仿真模型构建与配置：

   • 利用收集到的数据构建 IEEE33 节点配电网的仿真模型。
   • 设置负荷出力和日前-日内的 PV 预测出力，将其作为仿真模型的输入。
   • 设定网络综合运行费用权重 μOP 和网络损耗权重 μL 为 0.7 和 0.3。

4. 仿真运行及结果分析：

   • 将生成的PV出力场景和负荷出力应用于仿真模型，进行日前-日内的电力系统仿真运行。
   • 计算系统综合运行费用，并考虑网络损耗权重进行综合分析。
   • 分析节点电压幅值范围是否在合理范围内，并评估系统的稳定性和经济性。

以下是一个简化的伪代码示例，展示了如何生成PV出力场景，并进行简单的仿真模拟。这里使用 Python 语言作为示例：

import numpy as np

# 步骤1: 数据准备
# 收集 IEEE33 节点配电网的节点负载和支路阻抗参数
# ...

# 收集调控设备相关参数和其他附录中的数据
# ...

# 定义功率基准值和电压基准值
base_power = 10  # 10 MVA
base_voltage = 12.66  # 12.66 kV

# 定义节点电压幅值范围
voltage_range = (0.93, 1.07)  # 0.93p.u. ~ 1.07p.u.

# 步骤2: PV出力场景生成
# 生成日前PV预测出力值的平均值和标准差
average_forecast_output = 100  # 假设的平均值
std_deviation = 0.1 * average_forecast_output  # 标准差为平均值的10%

# 生成PV出力场景
num_scenarios = 100  # 生成场景的数量
pv_output_scenarios = np.random.normal(average_forecast_output, std_deviation, num_scenarios)

# 步骤3: 仿真模型构建与配置
# 在实际情况中，可能需要使用专业的仿真库或软件来构建电力系统模型

# 假设有一个简单的电力系统模型的类
class PowerSystemSimulator:
    def __init__(self, base_power, base_voltage):
        self.base_power = base_power
        self.base_voltage = base_voltage

    def simulate(self, pv_output, load_profile):
        # 在此添加电力系统仿真的逻辑
        # 包括节点电压计算、潮流分析、损耗计算等
        # 返回仿真结果，如综合运行费用等
        simulated_result = simulate_power_flow(pv_output, load_profile, self.base_power, self.base_voltage)
        return simulated_result

# 步骤4: 仿真运行及结果分析
# 创建电力系统仿真器实例
simulator = PowerSystemSimulator(base_power, base_voltage)

# 遍历PV出力场景并进行仿真
for scenario in pv_output_scenarios:
    # 假设load_profile是一个负荷出力的数组，具体根据实际情况准备数据
    load_profile = prepare_load_profile()

    # 进行仿真运行
    simulation_result = simulator.simulate(scenario, load_profile)

    # 在这里进行结果分析
    analyze_simulation_result(simulation_result)

在实际应用中，仿真的复杂性和详细步骤取决于所用的仿真软件和模型的复杂性。上述示例代码是一个简单的框架，需要根据实际情况进行调整和扩展。